Die Vermessung ist ein wesentlicher Vorschritt für alle Bauarbeiten.
Der gesamte Lageplan bestimmt die Struktur eines Gebäudes oder eines Geländes. Wir haben zahlreiche Vermessungsmethoden, um die Natur eines Grundstücks zu verstehen.
- Kette Vermessung
- Flugzeug Tisch Vermessung
- Kompass Vermessung
- Topographische Vermessung etc
Alle es tut ist aufnahme die tatsächlichen messungen in ein papier für einfache berechnung von bereich. Aber wie berechnet man die Grundstücksfläche?
Wie berechnet man die Grundstücksfläche?
Die Fläche ist nichts anderes als ein Raum, der von einer geometrischen Form eingenommen wird. Für grundlegende Flächenberechnungen könnten wir die folgenden Formeln verwenden.
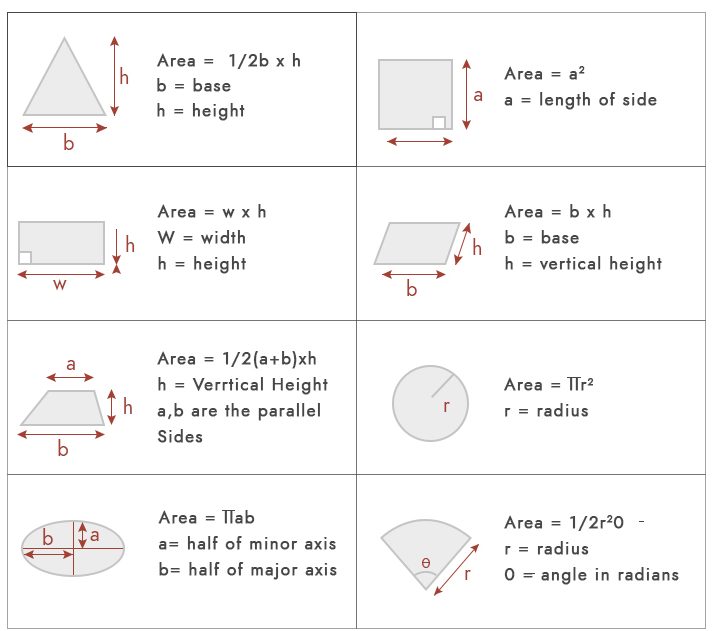
In der Praxis fällt der größte Teil der Handlung jedoch nicht unter diese geometrischen Formen. Die häufigsten Arten von Grundstücksflächen sind
- Dreieckiges Grundstück
- Unregelmäßige Polygone
- Quadratisch oder rechteckig
Zur Veranschaulichung der Formeln, vorausgesetzt, wir haben verschiedene Formen von Grundstücken.
Dreiecksdiagramm
Angenommen, wir haben ein Dreieck von 40 Fuß Basis & Breite.
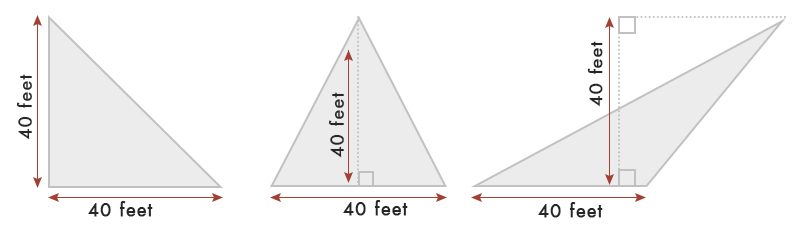
Gemäß der Tabelle, Fläche des Dreiecks = ½ x Basis x Breite = ½ x 40 x 40 = 80 Sq.ft
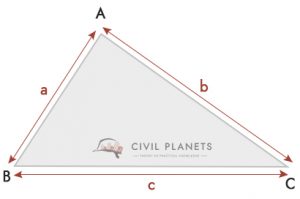
Wenn Sie die Höhe des Dreiecks nicht messen können und es sich nicht um einen rechten Winkel handelt, können Sie die folgende Formel verwenden
![]()
Wobei S = Umfang des Dreiecks = (a + b + c)/2
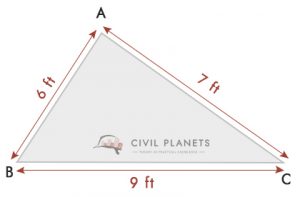
Aus der Zeichnung, a = 6 Fuß, b = 9 Fuß & c = 7 Fuß, S = (6+9+7)/2 = 11
Daher Fläche des Grundstücks = √S(S-a)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft ≅ 21 Quadrat.ft
Unregelmäßige Polygone
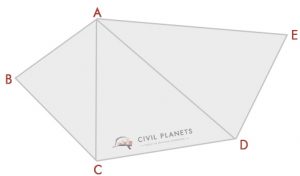
Die meisten von uns könnten diese Art von Handlung erkennen. Um die Fläche dieser Form zu finden, müssen wir die Trigonometrieberechnung verwenden. Es ist nicht so schwer.
Finden wir die Fläche dieser Form in zwei typischen Fällen
- Unregelmäßige Polygone (mit bekannten Schnittdimensionen)
- Unregelmäßige Polygone (mit Winkeln)
Unregelmäßige Polygone (mit bekannten Schnittdimensionen)
Stellen Sie sich vor, wir haben das folgende Diagramm mit bekannten Schnittdimensionen.
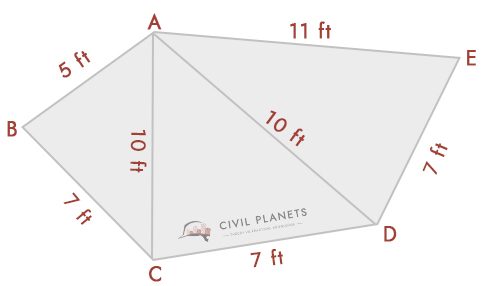
Mit der obigen Dreiecksformel können wir dies lösen. Aus dem Diagramm haben wir drei Dreiecke, nämlich ABC, ACD, & ADE
- Dreieck 1 – Δ ABC, wobei S = (5+7+10)/2 = 11
Formel für Fläche = √S(S-a)(S-b)(S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Dreieck 2 – Δ ACD, wobei S = (10+7+10)/2 = 13.5
Formel für Fläche = √S(S-a)(S-b)(S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Dreieck 3 – Δ ADE, wobei S = (10+7+11)/2 = 14
Formel für Fläche = √S(S-a)(S-b)(S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
Also Gesamtfläche der Form = 16.25+32.79+34.29 = 83,33 Quadratmeter.ft
Unregelmäßige Polygone (mit Winkeln)
Angenommen, wir kennen jetzt nicht die Schnittmessung, die nur Winkel wie unten hat
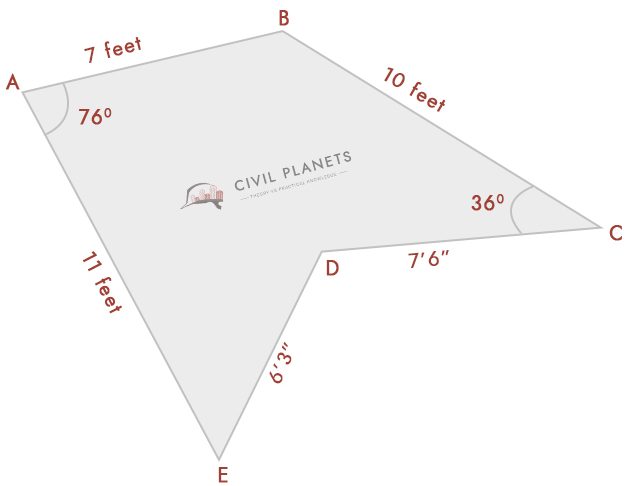
Trennen Sie nun das obige Bild in drei Dreiecke wie unten
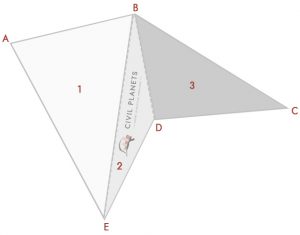
Jetzt haben wir 3 Dreiecke wie oben, nur etwas anstelle der Schnittdimension; Wir haben Winkel. Das erste ist also, dass wir die Schnittpunktmessung mit Trigonometrie berechnen müssen.
Die Schnittmessung kann durch Herons Formel erhalten werden c2 = a2 + b2 – 2abCos(C)
Wobei a = Länge von AB, b = Länge von AE, c = Länge von EB
Länge von EB = √(a2 + b2 – 2abCos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 füße
Länge von DB = √ (a2 + b2-2abCos (C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 fuß
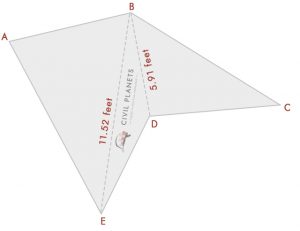
Jetzt kennen wir die Länge jeder Seite, mit der Dreiecksformel können wir jetzt die Fläche berechnen
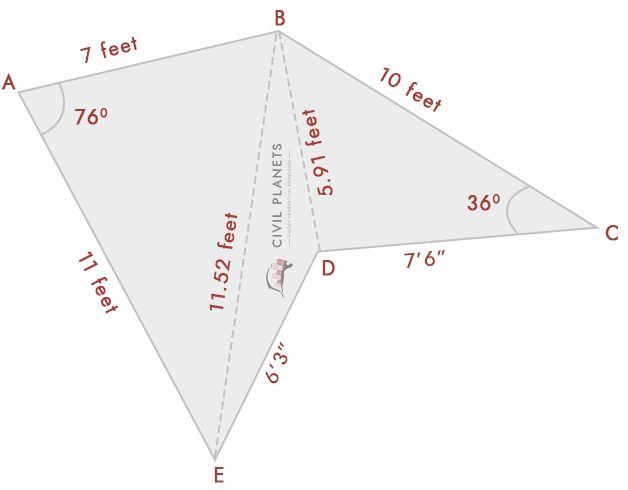
Aus dem Diagramm haben wir drei Dreiecke
Dreieck 1 – Δ ABE, wobei S = (7+11+11.52)/2 = 14.76
Formel für Fläche = √S(S-a)(S-b)(S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
Dreieck 2 – Bett, wobei S = (11.52+6.25+5.91)/2 = 11.84
Formel für Fläche = √S(S-a)(S-b)(S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
Dreieck 3 – Δ BDC, wobei S = (5.91+7.5+10)/2 = 11.70
Formel für Fläche = √S(S-a)(S-b)(S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
Also Gesamtfläche der Form = 37.35+11.21+21.99 = 70,55 Quadratmeter.ft
Glückliches Lernen 🙂
