
 |
Services offerts ce numéro
> L’Évaluateur Coach |
Note de l’éditeur: Cette histoire se trouve dans la nouvelle édition imprimée de Working RE (qui vient d’être envoyée par la poste). Suis-je un abonné RE qui travaille? OREP E& O Les assurés bénéficient d’un abonnement gratuit.
Quelle Est La Valeur Ajoutée De Cette Chambre Supplémentaire? (Comprendre la régression)
Par le Dr Keying Ye
Dans les termes les plus simples, les évaluateurs immobiliers évaluent la juste valeur marchande d’une propriété — un nombre qui agrège la valeur d’un large éventail de caractéristiques de la propriété, à la fois quantitatives (nombre de chambres et de salles de bains, superficie en pieds carrés, taille du terrain, nombre de garages, etc.) et qualitatives (vues, scène de rue, emplacement, etc.). Pas vrai?
Une façon d’approximer cette valeur est d’utiliser la méthode de régression, qui est un outil d’analyse de données pour étudier la relation entre une variable dépendante (dans ce cas, la valeur de la propriété) et des prédicteurs de caractéristiques (tels que le nombre de salles de bains ou la surface habitable brute). Cet article vise à montrer comment la régression peut augmenter la précision de l’évaluation en se concentrant sur les deux types les plus courants: Régression linéaire simple vs Régression linéaire multiple.
S’attaquer à la régression linéaire simple
La régression linéaire simple (SLR) est une approche de régression simple utilisant un seul prédicteur et une variable dépendante. Par exemple, si nous croyons que nous pouvons utiliser la surface habitable comme seul prédicteur pour estimer la valeur d’une propriété et que l’association entre la surface habitable et la valeur d’une propriété est linéairement liée, alors nous pourrions utiliser une simple régression linéaire pour estimer la valeur.
Une structure prédictive du REFLEX peut être exprimée en fonction prediction=m+b*.
Dans ce cas, la caractéristique est la variable indépendante et la prédiction est la variable de réponse (pensez à y = m + bx de l’algèbre du lycée). Ici, « m » et « b » sont respectivement la « pente » et l' »interception » d’un graphe fabriqué à partir de cette équation. L’interception est l’endroit où la prédiction serait si l’entité est nulle (si la propriété objet n’a pas de garage par exemple). La pente est l’augmentation ou la diminution de la valeur de la propriété pour chaque changement d’unité de l’entité (par exemple, combien la valeur de la propriété change pour chaque pied carré ajouté ou soustrait).
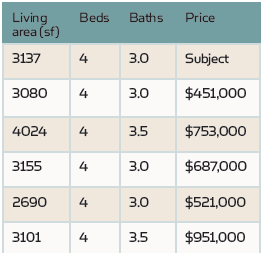
Considérons l’exemple suivant. Nous voulons prévoir la valeur d’une résidence unifamiliale (SFR) et nous connaissons ses informations de base telles que la surface habitable, le nombre de lits et le nombre de salles de bains. En utilisant l’analyse comps pré-calculée de HouseCanary, nous identifions les cinq propriétés les plus similaires vendues au cours des six derniers mois, comme le montre le tableau ci-dessous.
(l’histoire continue ci-dessous)
( l’histoire continue)
La similitude est déterminée par les types de propriété (SFR ou autres), les caractéristiques de propriété et les distances géographiques entre ces propriétés et la propriété en question. Comme chaque propriété a le même nombre de chambres, cette caractéristique n’a aucun impact sur le prix parmi ces propriétés autre que comme une constante fixe. La variation de prix, cependant, est clairement associée à la surface habitable et au nombre de bains.
Les chiffres ci-dessous montrent la relation entre les prix de l’immobilier et soit la surface habitable, soit le nombre de bains de chacune des propriétés (voir les parcelles 1 et 2). Dans chaque graphique, le point où la ligne brune verticale touche l’axe horizontal montre la valeur de la propriété en question pour l’élément en question (3 137 pour la surface habitable et 3,0 pour les salles de bains). La ligne bleue est la ligne de régression linéaire à un prédicteur, qui montre la relation prédictive entre le prix de la propriété et la caractéristique appropriée.
(l’histoire continue ci-dessous)
( l’histoire continue)
Dans la parcelle 1, par exemple, la relation de prévision entre le prix et la surface habitable est exprimée comme suit: prix = 200 323 + 147 * surface habitable. Pour la propriété en question, qui mesure 3 137 pieds carrés, cela signifie que son prix prévu est $661,462: $661,462 = ($200,323 + $147 * 3137) Ceci est montré comme le point bleu solide dans le graphique de la parcelle 1. La » pente » de la droite de régression, 147, mesure la valeur du prix unitaire, c’est-à-dire l’ajustement du prix pour chaque pied carré supplémentaire (graphique 1). Cependant, si nous utilisons le nombre de salles de bains comme prédicteur à la place, le prix prévu de la propriété cible est $553,000 (-$1,241,000 + $598,000 * 3.0 = $553,000). Cet écart dans le prix prévu (661 462$ et 553 000 $) est courant lors de l’utilisation de formules de régression linéaire simples pour différentes caractéristiques d’une même propriété (voir graphique du graphique 2 ci-dessus).
Le prix réel de la propriété cible est de 607 000 $, ce qui est indiqué sous la forme d’une étoile brune dans chaque graphique. Par conséquent, les erreurs pour les deux estimations sont presque identiques, bien que dans la direction opposée, qu’elles soient exprimées en dollars bruts ($607,000 – $661,462 = -$54,462 et 607 000 $ – 553 000 = = 54 000 respectively, respectivement) ou en pourcentage (-$54,462/$607,000 = – 9 pourcentage et 54 000 $ / 607 000 = = 9 %, respectivement).
Aller plus loin avec la Régression linéaire multiple
En utilisant une régression linéaire simple, un évaluateur peut utiliser le prédicteur le plus important de la valeur d’une propriété pour effectuer son analyse d’évaluation (ou même utiliser une analyse SLR sur plusieurs entités pour obtenir plusieurs points de référence. Mais que se passe-t-il si le prédicteur le plus important n’est pas clair? Que se passe-t-il si, par exemple, toutes les unités de trois chambres dans une analyse donnée ont un nombre différent de salles de bains, différentes surfaces de vie brutes, ou seulement quelques-unes d’entre elles ont des piscines? En utilisant la régression linéaire multiple (MLR), les évaluateurs peuvent comparer l’effet de plusieurs prédicteurs sur la valeur d’une propriété avec un seul calcul.
Une structure prédictive de MLR peut être exprimée comme suit:
prédiction = m + b1 * caractéristique 1 + b2 * caractéristique 2 + b3 * caractéristique 3 +
Par exemple, avec les données ci-dessus, nous pouvons régresser le prix à la fois par surface habitable et par nombre de salles de bains: prix = – 1 309 770$ – 1251 * surface habitable + 744 918 baths * bains.
Si nous branchons les valeurs de fonctionnalité de la propriété cible, le prix prévu est de 532 859 $, ce qui donne une erreur de 74 141 $ ou 12%. L’erreur de cette prédiction est pire que les erreurs considérées dans les reflex, mais ne vous inquiétez pas, il y a une explication dans les données (et une solution qui suit!).
Tout d’abord, nous devons considérer les relations entre les prédicteurs eux-mêmes et comprendre quelles informations les lettres de l’équation ci-dessus transmettent, ce qui n’est pas aussi simple dans ce cas que lors de l’utilisation du REFLEX. Par exemple, le coefficient – 125$ pour la surface habitable indique que, pour un nombre fixe de bains, l’augmentation de la surface habitable d’un pied carré diminue en fait le prix de la propriété de 125 $ — ce qui ne semble pas naturel! Cependant, si nous regardons le tableau ci-dessus, nous pouvons voir que pour 3,5 salles de bain, il y aseulement deux propriétés. Celui avec 3 101 pieds carrés est en fait plus cher (951 000$) que la propriété avec 4 024 pieds carrés. Pour les trois propriétés avec salles de bains 3.0, les surfaces habitables (2690, 3080, 3155) ne sont pas exactement en corrélation avec les prix ($521,000, $451,000, $687,000) soit.
(l’histoire continue ci-dessous)

( l’histoire continue)
Cela signifie que, dans nos données, nous avons une relation linéaire différente entre le prix de réponse et la surface habitable prédictive pour les propriétés avec un nombre différent de salles de bains. Ainsi, dans le graphique suivant ci-dessous, la ligne noire (la ligne de régression avec bains = 3,0) et la ligne rouge (la ligne de régression avec bains = 3,5) montrent en fait des tendances opposées. Dans un tel cas, les deux prédicteurs ne sont pas purement additifs par rapport au prix — une augmentation d’unne signifie pas immédiatement une augmentation du prix. Le remède à cela est d’ajouter un autre terme, surface habitable * nombre de bains, qui représente l’interaction des prédicteurs.
(l’histoire continue ci-dessous)
( l’histoire continue)
Pour nos données, la relation prédictive serait exprimée comme suit:
prix = – 9 590 000$ + 2 552 area * surface habitable + 3 202 000 * bains – 791
* surface habitable * bains
Cela donne une prédiction de propriété cible de 577 523 $, qui a une erreur de $29,477 ($607,000 – $577,523 = $29,477) et une erreur relative de 5%, ce qui est le meilleur ajustement jusqu’à présent!
Quand utiliser Simple vs. Régression linéaire multiple
Lors de l’évaluation d’une propriété ou de la détermination de la valeur d’une caractéristique particulière, les évaluateurs peuvent utiliser l’analyse de régression pour obtenir les ajustements de prix les plus précis en tenant compte de l’effet de plusieurs caractéristiques sur la valeur d’une propriété. Les nouvelles réglementations de l’industrie exigeant une justification fondée sur les données pour les décisions d’évaluation pourraient rendre l’analyse de régression encore plus nécessaire pour les évaluateurs dans un avenir proche.
Gardez à l’esprit qu’il n’est pas toujours possible d’utiliser une analyse de régression linéaire multiple. Si, par exemple, il n’y a pas un éventail varié de points de données disponibles pour une propriété et ses comparables, il se peut qu’il n’y ait pas suffisamment d’informations pour effectuer une analyse MLR. Mais, lorsqu’il y a suffisamment de données disponibles pour effectuer une analyse MLR, elle produit souvent les résultats les plus précis. Rappelez-vous qu’il y a des moments où une analyse MLR nécessitera un terme supplémentaire qui représente l’interaction des prédicteurs pour être la plus précise, comme dans l’exemple ci-dessus. Bien que l’analyse de régression ne remplace clairement pas l’expertise d’un évaluateur, elle peut être un complément précieux à celle—ci.
Nous espérons que ces informations vous seront utiles pour vos évaluations.
> CE En ligne – 7 Heures (approuvé dans 40 États)
Comment Soutenir et prouver Vos ajustements
Présenté par: Richard Hagar, SRA
Pratiques commerciales incontournables pour tous les évaluateurs travaillant aujourd’hui. Assurez un soutien approprié pour vos ajustements. Faire des ajustements défendables est la première étape pour devenir un évaluateur de « niveau Un », qui gagne plus, profite des meilleures affectations et subit moins d’accrocs et de rappels. Améliorez votre jeu, évitez les rappels fastidieux et gagnez du CE approuvé aujourd’hui! Inscrivez-Vous Maintenant! 119 $ (7 Heures)
Prix de l’assuré OREP: 99 $
À propos de l’auteur
Le Dr Keying Ye est professeur de statistiques au College of Business de l’Université du Texas à San Antonio et également chercheur principal chez HouseCanary où il développe des analyses prédictives pour son logiciel d’évaluation leader, son évaluateur HouseCanary et d’autres produits. HouseCanary Appraiser aide les évaluateurs résidentiels à fermer plus d’affaires grâce à une solution facile à utiliser et comprend des formulaires tels que 1004, 2055, 1075 et plus encore!
