pomiary są niezbędnym wstępnym etapem prac budowlanych.
cały plan działki określa strukturę budynku lub Działki. Mamy wiele metod geodezyjnych, aby zrozumieć naturę działki.
- pomiary łańcuchowe
- pomiary z tabeli Lotniczej
- pomiary z kompasu
- pomiary topograficzne itp
wszystko, co robi, to zapisywanie rzeczywistych pomiarów na papierze w celu łatwego obliczenia powierzchni. Ale jak obliczyć powierzchnię działki?
Jak obliczyć powierzchnię działki?
obszar jest niczym innym jak przestrzenią zajmowaną przez dowolny kształt geometryczny. Do podstawowych obliczeń powierzchni możemy użyć poniższych wzorów.
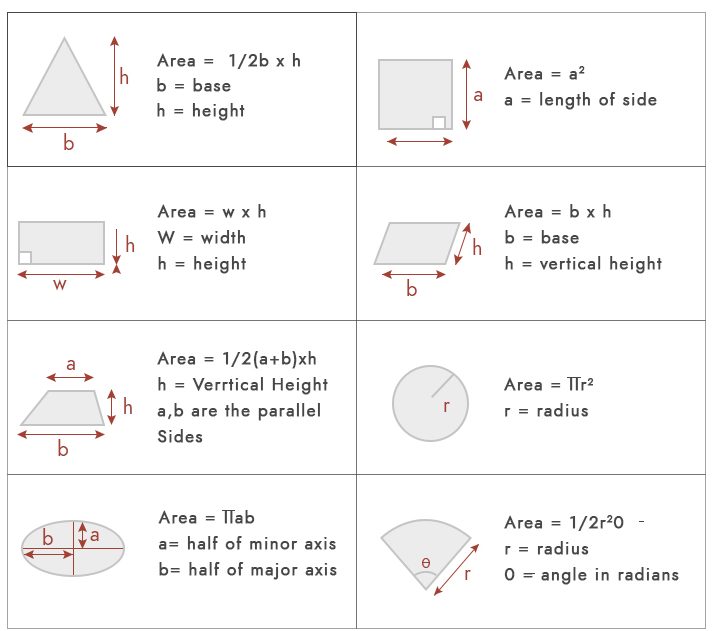
ale w praktyce, większość fabuły nie mieszczą się w tych geometrycznych kształtach. Najczęstsze typy obszarów działki są
- Trójkątny działki
- nieregularne wielokąty
- kwadratowy lub prostokątny
do zilustrowania wzorów, zakładając, że mamy różne kształty działek.
Wykres trójkąta
zakładając, że mamy trójkąt o podstawie 40 stóp & szerokości.
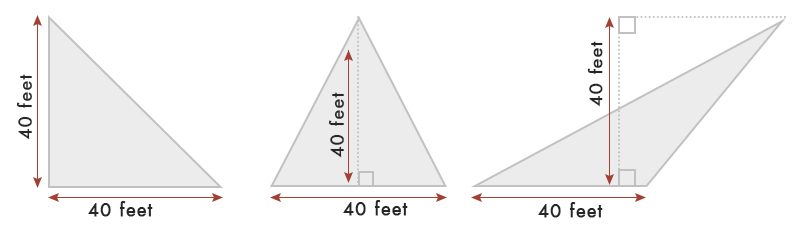
zgodnie z tabelą, Powierzchnia trójkąta = ½ x podstawa x szerokość = ½ x 40 x 40 = 80 Sq.WP
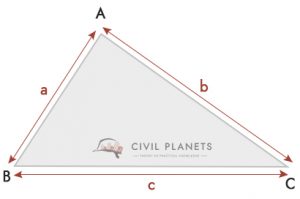
jeśli nie możesz zmierzyć wysokości trójkąta i jeśli nie jest to kąt prosty, możesz użyć poniższego wzoru
![]()
gdzie S = obwód trójkąta = (a + b + c)/2
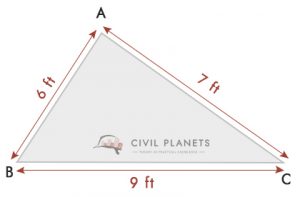
z rysunku, a = 6 stóp, b = 9 stóp & c = 7 stóp, S = (6+9+7)/2 = 11
zatem Powierzchnia działki = √s(S-a)(S-b) (S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft ≅ 21 m2ft
nieregularne wielokąty
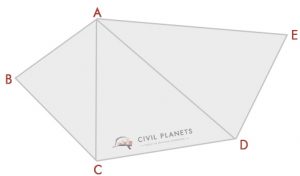
większość z nas potrafiła rozpoznać tego rodzaju spisek. Aby znaleźć pole tego kształtu, musimy użyć obliczeń trygonometrycznych. To nie takie trudne.
znajdźmy pole tego kształtu w dwóch typowych przypadkach
- wielokąty nieregularne (o znanych wymiarach przecięcia)
- wielokąty nieregularne (o kątach)
wielokąty nieregularne (o znanych wymiarach przecięcia)
wyobraź sobie, że mamy następujący wykres, o znanych wymiarach przecięcia.
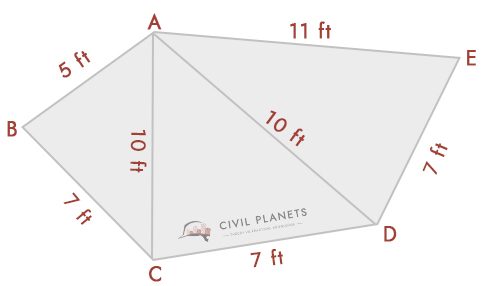
korzystając z powyższego trójkątnego wzoru, możemy to rozwiązać. Z diagramu mamy trzy trójkąty: ABC, ACD, & ADE
- Trójkąt 1-Δ ABC, gdzie S = (5+7+10)/2 = 11
wzór na powierzchnię = √s(S-a)(S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Trójkąt 2-Δ ACD, gdzie S = (10+7+10)/2 = 13.5
wzór na powierzchnię = √s(S-a)(S-b) (S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Trójkąt 3-Δ ADE, gdzie S = (10+7+11)/2 = 14
wzór na powierzchnię = √s(S-a)(S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
so total area of the shape = 16.25+32.79+34.29 = 83.33 m2ft
wielokąty nieregularne (z kątami)
zakładając, że teraz nie znamy pomiaru przecięcia tylko o kątach takich jak na zdjęciu poniżej
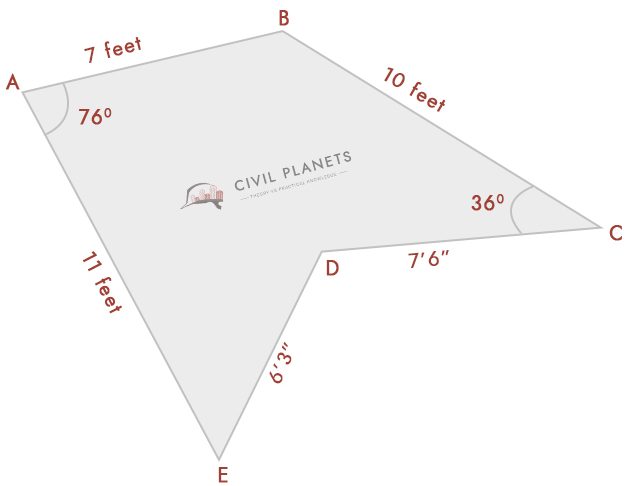
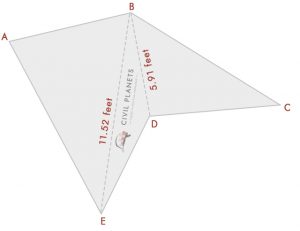
teraz oddziel powyższy obraz na trzy trójkąty, jak poniżej
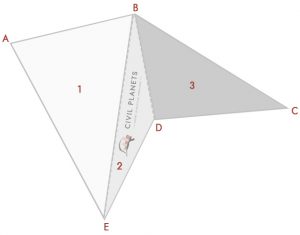
teraz mamy 3 trójkąty, jak wyżej, tylko zamiast wymiaru przecięcia, mamy kąty. Pierwszą rzeczą jest obliczenie miary przecięcia za pomocą trygonometrii.
pomiar przecięcia można uzyskać wzorem Herona c2 = a2 + b2-2abcos(C)
gdzie, A = długość AB, b = Długość AE, c = Długość EB
Długość EB = √(a2 + b2 – 2abcos (C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 stopy
Długość DB = √(a2 + b2-2abcos (C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 stóp
teraz znamy długość każdego boku, korzystając ze wzoru trójkąta, możemy obliczyć Pole teraz
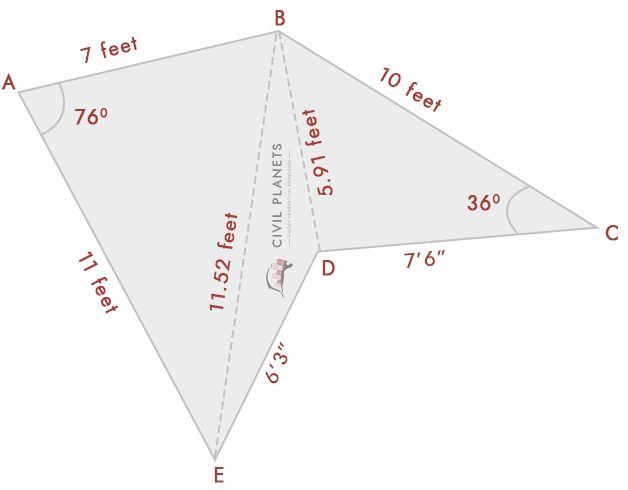
z diagramu mamy trzy trójkąty
Trójkąt 1-Δ ABE, gdzie S = (7+11+11.52)/2 = 14.76
wzór na powierzchnię = √s(S-a)(S-b) (S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
trójkąt 2-Δ łóżko, gdzie S = (11.52+6.25+5.91)/2 = 11.84
wzór na powierzchnię = √s(S-a)(S-b) (S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
Trójkąt 3-Δ BDC, gdzie S = (5.91+7.5+10)/2 = 11.70
wzór na powierzchnię = √s(S-a)(S-b) (S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
so total area of the shape = 37.35+11.21+21.99 = 70.55 m2ft
Happy Learning 🙂
