
 |
diensten aangeboden deze uitgave
> de taxateur Coach |
Noot van de redactie: Dit verhaal is te vinden in de nieuwe gedrukte editie van Working RE (net gemaild). Ben ik een werkende opnieuw abonnee? OREP e&o verzekerden genieten een gratis abonnement.
Hoeveel Waarde Voegt Die Extra Slaapkamer Toe? (Understanding Regression)
door Dr. Keying Ye
in de eenvoudigste termen, taxateurs van onroerend goed evalueren de reële marktwaarde van een onroerend goed — een getal dat de waarde van een breed scala van kenmerken van het onroerend goed aggregeert, zowel kwantitatief (aantal slaapkamers en badkamers, vierkante meters, kavelgrootte, aantal garages, enz.) en kwalitatief (uitzicht, straatbeeld, locatie, enz.). Toch?
een manier om deze waarde te schatten is het gebruik van de regressiemethode, een data-analysetool voor het bestuderen van de relatie tussen een afhankelijke variabele (in dit geval de waarde van de eigenschap) en functievoorspellers (zoals het aantal badkamers of het bruto woonoppervlak). Dit artikel is bedoeld om te laten zien hoe regressie beoordeling nauwkeurigheid kan verhogen door zich te concentreren op de twee meest voorkomende types: eenvoudige Versus meerdere lineaire regressie.
het aanpakken van eenvoudige lineaire regressie
eenvoudige lineaire regressie (SLR) is een eenvoudige regressiebenadering waarbij slechts één voorspeller en één afhankelijke variabele worden gebruikt. Bijvoorbeeld, als we geloven dat we het woongebied als enige voorspeller kunnen gebruiken om de waarde van een eigenschap te schatten en dat de associatie tussen het woongebied en de waarde van een eigenschap lineair gerelateerd is, dan kunnen we een eenvoudige lineaire regressie gebruiken om de waarde te schatten.
een voorspellende structuur van SLR kan worden uitgedrukt als prediction = m + b * feature.
in dit geval is feature de onafhankelijke variabele en voorspelling is de responsvariabele (denk terug aan y = m + bx uit de middelbare school algebra). Hier” m “en” b “zijn de” helling “en” intercept, ” respectievelijk, van een grafiek gemaakt van deze vergelijking. De intercept is waar de voorspelling zou zijn als de functie nul is (als de eigenschap van het onderwerp geen garage heeft bijvoorbeeld). De helling is de toename of afname van de waarde van de eigenschap voor elke eenheid verandering in de functie (bijvoorbeeld hoeveel de waarde van de eigenschap verandert voor elke vierkante voet toegevoegd of afgetrokken).
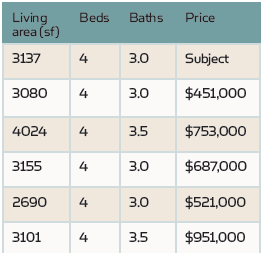
neem het volgende voorbeeld. We willen de waarde van een eengezinswoning (SFR) voorspellen en we kennen de basisinformatie zoals woonoppervlakte, aantal bedden en aantal baden. Met behulp van HouseCanary ‘ s pre-computed comps analyse, identificeren we de vijf meest vergelijkbare woningen verkocht in de afgelopen zes maanden, zoals weergegeven in de tabel hieronder.
(verhaal gaat verder hieronder)
(story continues)
de Overeenkomst wordt bepaald door eigenschapstypen (SFR of andere), eigenschapskenmerken en de geografische afstanden tussen deze eigenschappen en de eigenschap van het onderwerp. Aangezien elke woning hetzelfde aantal slaapkamers heeft, heeft deze functie geen invloed op de prijs van deze woningen anders dan als een vaste constante. De prijsvariatie wordt echter duidelijk geassocieerd met het woongedeelte en het aantal baden.
onderstaande cijfers geven het verband weer tussen de vastgoedprijzen en de woonoppervlakte of het aantal baden van elk van de woningen (zie de percelen 1 en 2). In elke grafiek toont het punt waar de verticale bruine lijn de horizontale as raakt de waarde van de eigenschap van het onderwerp voor de functie in kwestie (3.137 voor woonruimte en 3.0 voor badkamers). De blauwe lijn is de lineaire regressielijn met één voorspeller, die de voorspellende relatie tussen de vastgoedprijs en de juiste functie weergeeft.
(verhaal gaat verder hieronder)
(in plot 1 bijvoorbeeld wordt de voorspellende relatie tussen prijs en woonoppervlakte uitgedrukt als: prijs = 200.323 + 147 * woonoppervlakte. Voor het onderwerp eigenschap, die 3,137 vierkante voet meet, betekent dit de voorspelde prijs is $661,462: $661,462 = ($200,323 + $147 * 3137) dit wordt weergegeven als de effen blauwe stip in de plot 1 grafiek. De” helling ” van de regressielijn 147 meet de prijs per eenheid, d.w.z. de prijsaanpassing voor elke extra vierkante voet (perceel 1). Echter, als we gebruik maken van het aantal badkamers als onze voorspeller in plaats daarvan, het doel woning voorspelde prijs is $553,000 (-$1,241,000 + $598,000 * 3.0 = $553,000). Deze discrepantie in voorspelde prijs ($661.462 en $ 553.000) is gebruikelijk bij het gebruik van eenvoudige lineaire regressie formules voor verschillende kenmerken van dezelfde eigenschap (zie plot 2 grafiek hierboven).
de werkelijke prijs voor de doeleigenschap is $ 607.000, die wordt weergegeven als een bruine ster in elke grafiek. Bijgevolg zijn de fouten voor beide ramingen vrijwel identiek, zij het in tegenovergestelde richting, al dan niet uitgedrukt in ruwe dollars ($607,000 – $661,462 = -$54,462 en $607,000 – $ 553,000 = $ 54,000, respectievelijk) of als percentage (-$54,462/$607,000 = – 9 procent en$54.000/ $ 607.000 = 9 procent, respectievelijk).
ga verder met meervoudige lineaire regressie
gebruikmakend van eenvoudige lineaire regressie, kan een taxateur de belangrijkste voorspeller van de waarde van een eigenschap gebruiken om zijn/haar taxatieanalyse te maken (of zelfs SLR-analyse op meerdere kenmerken gebruiken om meerdere referentiepunten te krijgen. Maar wat als de belangrijkste voorspeller niet duidelijk is? Wat als, bijvoorbeeld, alle van de drie slaapkamers eenheden in een gegeven analyse hebben een ander aantal badkamers, variërende bruto woonoppervlakken, of slechts een paar van hen hebben zwembaden? Door gebruik te maken van meerdere lineaire regressie (MLR) taxateurs kunnen het effect dat meerdere voorspellers hebben op een eigenschap waarde te vergelijken met een enkele berekening.
een voorspellende structuur van MLR kan worden uitgedrukt als:
prediction = m + b1 * feature 1 + b2 * feature 2 + b3 * feature 3+ …
bijvoorbeeld, met de bovenstaande gegevens kunnen we de prijs regresseren naar zowel het woonoppervlak als het aantal badkamers: price = – $ 1.309.770 – $125 * living area + $ 744.918 * badkamers.
als we de functiewaarden van de doeleigenschap inpluggen, is de voorspelde prijs $532.859, wat een fout oplevert van $74.141 of 12%. De fout van deze voorspelling is erger dan die fouten beschouwd in spiegelreflexcamera ‘ s, maar maak je geen zorgen, er is een verklaring in de gegevens (en een oplossing die volgt!).
eerst moeten we kijken naar de relaties tussen de voorspellers zelf en begrijpen welke informatie de letters in de vergelijking hierboven geven, wat in dit geval niet zo eenvoudig is als bij het gebruik van SLR. Bijvoorbeeld, de coëfficiënt -$125 voor de woonkamer zegt dat, Voor een vast aantal baden, het verhogen van het woonoppervlak met een vierkante voet eigenlijk vermindert de prijs van het onroerend goed met $ 125-wat onnatuurlijk lijkt! Echter, als we kijken naar de bovenstaande tabel, kunnen we zien dat voor 3,5 badkamers, zijn er slechts twee eigenschappen. Degene met 3.101 vierkante voet is eigenlijk duurder ($951.000) dan het pand met 4.024 vierkante voet. Voor de drie woningen met 3.0 badkamers, de woonruimtes (2690, 3080, 3155) niet precies correleren met de prijzen ($521,000, $451,000, $687,000) beide.
(verhaal gaat verder hieronder)

(story continues)
dit betekent dat we in onze gegevens een andere lineaire relatie hebben tussen de responsprijs en de voorspeller voor de woningen met een ander aantal badkamers. In de volgende grafiek hieronder laten de zwarte lijn (de regressielijn met baden = 3.0) en de rode lijn (de regressielijn met baden = 3.5) in feite tegengestelde trends zien. In een dergelijk geval zijn beide voorspellers niet louter additief ten opzichte van de prijs—een verhoging van één betekent niet onmiddellijk een stijging van de prijs. De remedie hiervoor is om een andere term toe te voegen, woonoppervlak * aantal baden, die de interactie van de voorspellers vertegenwoordigt.
(verhaal gaat verder hieronder)
(story continues)
voor onze gegevens zou de voorspellende relatie worden uitgedrukt als:
prijs = – $ 9.590.000 + $ 2.552 * woonoppervlak + 3.202.000 * badkamers-791
* woonoppervlak * badkamers
dit levert een voorspelling van de doeleigenschappen op van $ 577.523, wat een fout heeft van $29,477 ($607,000 – $577,523 = $29,477) en een relatieve fout van 5 procent, dat is de beste pasvorm tot nu toe!
wanneer Simple vs. Meervoudige lineaire regressie
bij het taxeren van een onroerend goed of het bepalen van de waarde van een bepaald kenmerk, kunnen taxateurs regressieanalyse gebruiken om de meest nauwkeurige prijsaanpassingen af te leiden door rekening te houden met het effect van meerdere kenmerken op de waarde van een onroerend goed. Nieuwe regelgeving voor de sector die gegevensgestuurde rechtvaardiging vereist voor beoordelingsbeslissingen kan regressieanalyse in de nabije toekomst nog noodzakelijker maken voor taxateurs.
Houd er rekening mee dat het niet altijd mogelijk is een meervoudige lineaire regressieanalyse te gebruiken. Als er bijvoorbeeld geen gevarieerde reeks datapunten beschikbaar is voor een eigenschap en zijn comparables, is er misschien niet genoeg informatie om een MLR-analyse uit te voeren. Maar wanneer er voldoende gegevens beschikbaar zijn om een MLR-analyse uit te voeren, levert dit vaak de meest nauwkeurige resultaten op. Vergeet niet dat er momenten zijn waarop een MLR-analyse een extra term vereist die de interactie van de voorspellers vertegenwoordigt om het meest accuraat te zijn, zoals in het voorbeeld hierboven. Hoewel regressieanalyse duidelijk de expertise van een taxateur niet vervangt, kan het een waardevolle aanvulling daarop zijn.
wij hopen dat u deze inzichten nuttig zult vinden voor uw beoordelingen.
> CE Online-7 Hours (approved in 40 states)
How to Support and Prove Your Adjustments
Presented by: Richard Hagar, SRA
Must-know business practices for all taxateurs working today. Zorg voor een goede ondersteuning voor uw aanpassingen. Het maken van verdedigbare aanpassingen is de eerste stap in het worden van een “Tier One” taxateur, die meer verdient, geniet van de beste opdrachten en lijdt minder problemen en callbacks. Up your game, vermijd tijdrovende callbacks en verdien goedgekeurd CE vandaag! Schrijf Je Nu In! $119 (7 uur)
OREP verzekerde prijs: $ 99
over de auteur
Dr. Keying Ye is hoogleraar Statistiek aan het College Of Business in de Universiteit van Texas in San Antonio en tevens Senior Onderzoeker bij HouseCanary, waar hij predictive analytics ontwikkelt voor zijn toonaangevende Taxatiesoftware, Housecanary taxateur en andere producten. HouseCanary taxateur helpt residentiële taxateurs sluiten meer business door middel van een eenvoudig te gebruiken oplossing en omvat formulieren zoals 1004, 2055, 1075, en meer!
