
 |
Services tilbudt dette spørgsmål
>taksator Coach |
Redaktørens Note: Denne historie kan findes i den nye trykte udgave af arbejder RE (bare sendt). Er jeg en arbejdende re abonnent? OREP E&o forsikrede nyder et gratis abonnement.
Hvor Meget Værdi Tilføjer Det Ekstra Soveværelse? (Forståelse Regression)
af Dr. Keying Ye
i de simpleste vendinger, fast ejendom bedømmere vurdere dagsværdien af en ejendom — et tal, der aggregerer værdien af en bred vifte af ejendommens funktioner, både kvantitativ (antal soveværelser og badeværelser, firkantede optagelser, parti størrelse, antal garager, etc.) og kvalitative (visninger, gadescene, placering, etc.). Ikke?
en måde at tilnærme denne værdi på er at bruge regressionsmetoden, som er et dataanalyseværktøj til at studere forholdet mellem en afhængig variabel (i dette tilfælde ejendomsværdi) og funktionsprediktorer (såsom antal badeværelser eller brutto opholdsstue). Denne artikel har til formål at vise, hvordan regression kan øge vurderingsnøjagtigheden ved at fokusere på de to mest almindelige typer: Enkel vs. Multiple lineær Regression.
håndtering af simpel lineær Regression
simpel lineær regression (SLR) er en ligetil regressionstilgang, der kun bruger en forudsigelse og en afhængig variabel. For eksempel, hvis vi mener, at vi kan bruge boligareal som den eneste forudsigelse til at estimere en ejendoms værdi, og at sammenhængen mellem boligareal og værdien af en ejendom er lineært relateret, så kunne vi bruge en simpel lineær regression til at estimere værdien.
en forudsigelig struktur af spejlreflekskamera kan udtrykkes som forudsigelse = m + b * funktion.
i dette tilfælde er funktionen den uafhængige variabel, og forudsigelse er responsvariablen (tænk tilbage på y = m + BKS fra high school algebra). Her er “m” og “b” henholdsvis “hældning” og “aflytning” af en graf lavet af denne ligning. Aflytningen er, hvor forudsigelsen ville være, hvis funktionen er nul (hvis emnet ejendom ikke har en garage for eksempel). Hældningen er stigningen eller faldet i ejendomsværdien for hver enhedsændring i funktionen (f.eks. hvor meget ejendommens værdi ændres for hver kvadratfod, der tilføjes eller trækkes fra).
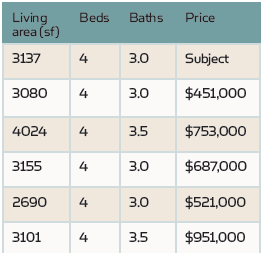
overvej følgende eksempel. Vi ønsker at forudsige værdien af en enkeltfamiliebolig (SFR), og vi kender dens grundlæggende oplysninger såsom opholdsstue, antal senge og antal bade. Ved hjælp af Housecanarys forudberegnede comps-analyse identificerer vi de fem mest lignende ejendomme, der sælges inden for de sidste seks måneder, som vist i nedenstående tabel.
(historien fortsætter nedenfor)
(historien fortsætter)
ligheden bestemmes af ejendomstyper (SFR eller andre), Ejendomsfunktioner og de geografiske afstande mellem disse egenskaber og emneegenskaben. Da hver ejendom har det samme antal soveværelser, har denne funktion ingen indflydelse på prisen blandt disse ejendomme bortset fra som en fast konstant. Prisvariationen er imidlertid tydeligt forbundet med opholdsstue og antallet af bade.
nedenstående tal viser forholdet mellem ejendomspriserne og enten boligarealet eller antallet af bade i hver af ejendommene (se plot 1 og 2). I hver graf viser det punkt, hvor den lodrette brune linje berører den vandrette akse, emnets egenskabs værdi for den pågældende funktion (3.137 for opholdsstue og 3,0 for badeværelser). Den blå linje er den lineære regressionslinje med en forudsigelse, der viser det forudsigelige forhold mellem ejendomsprisen og den relevante funktion.
(historien fortsætter nedenfor)
(historien fortsætter)
i plot 1 udtrykkes for eksempel prognoseforholdet mellem pris og boligareal som: pris =200.323 + 147 * boligareal. For emnet ejendom, som måler 3,137 kvadratfod, betyder det, at den forudsagte pris er $661,462: $661,462 = ($200,323 + $147 * 3137) dette vises som den solide blå prik i plot 1-grafen. Regressionslinjens “hældning”, 147, måler enhedsprisværdien, dvs.prisjusteringen for hver yderligere kvadratfod (plot 1). Imidlertid, hvis vi bruger antal badeværelser som vores forudsigelse i stedet, målejendommens forudsagte pris er $553,000 (-$1,241,000 + $598,000 * 3.0 = $553,000). Denne uoverensstemmelse i den forudsagte pris ($661.462 og $553.000) er almindelig, når du bruger enkle lineære regressionsformler til forskellige funktioner i den samme egenskab (se plot 2-graf ovenfor).
den faktiske pris for målejendommen er $607.000, som vises som en brun stjerne i hver graf. Følgelig er fejlene for begge estimater næsten identiske, omend i den modsatte retning, hvad enten de udtrykkes i rå dollars ($607,000 – $661,462 = -$54,462 og $ 607.000 – $553.000 = $54.000, henholdsvis) eller i procent (-$54,462/$607,000 = – 9 procent og $ 54.000 / $607.000 = henholdsvis 9 procent).
gå videre med multipel lineær Regression
ved hjælp af simpel lineær regression kan en taksator bruge den vigtigste forudsigelse for en ejendoms værdi til at foretage sin vurderingsanalyse (eller endda bruge SPEJLREFLEKSANALYSE på flere funktioner for at få flere referencepunkter. Men hvad nu hvis den vigtigste forudsigelse ikke er klar? Hvad hvis, for eksempel, alle de tre soveværelsesenheder i en given analyse har et andet antal badeværelser, varierende brutto boligarealer, eller kun et par af dem har puljer? Ved hjælp af multiple lineær regression (MLR) bedømmere kan sammenligne den effekt, at flere prædiktorer har på en egenskabsværdi med en enkelt beregning.
en forudsigelig struktur af MLR kan udtrykkes som:
prediction = m + b1 * feature 1 + b2 * feature 2 + b3 * feature 3+ …
for eksempel kan vi med ovenstående data regressere prisen med både opholdsstue og antal badeværelser: pris = -$1,309,770 – $125 * boligareal + $744,918 * bade.
hvis vi tilslutter målegenskabens funktionsværdier, er den forudsagte pris $532,859, hvilket giver en fejl på $74,141 eller 12%. Fejlen i denne forudsigelse er værre end de fejl, der overvejes i spejlreflekskameraer, men rolig, der er en forklaring i dataene (og en løsning, der følger!).
for det første skal vi overveje forholdet mellem forudsigerne selv og forstå, hvilke oplysninger bogstaverne i ligningen ovenfor formidler, hvilket ikke er så ligetil i dette tilfælde som ved brug af spejlreflekskamera. For eksempel koefficienten – $125 for den levende område siger, at for et fast antal bade, stigende boligareal med en kvadratfod faktisk nedsætter ejendomsprisen ved $125 — som synes unaturligt! Men hvis vi ser på tabellen ovenfor, kan vi se, at for 3,5 badeværelser er derkun to ejendomme. Den med 3.101 kvadratfod er faktisk dyrere ($951.000) end ejendommen med 4.024 kvadratfod. For de tre ejendomme med 3,0 badeværelser korrelerer boligarealerne (2690, 3080, 3155) ikke nøjagtigt med priserne ($521,000, $451,000, $687,000) heller ikke.
(historien fortsætter nedenfor)

(historien fortsætter)
dette betyder, at vi i vores data har et andet lineært forhold mellem responsprisen og forudsigelsesområdet for ejendommene med et andet antal badeværelser. I den næste graf nedenfor viser den sorte linje (regressionslinjen med bade = 3,0) og den røde linje (regressionslinjen med bade = 3,5) faktisk modsatte tendenser. I et sådant tilfælde er begge forudsigere ikke rent additive mod prisen—en stigning på enindebærer ikke umiddelbart en stigning i prisen. Løsningen til dette er at tilføje et andet udtryk, boligareal * antal bade, som repræsenterer forudsigernes interaktion.
(historien fortsætter nedenfor)
(historien fortsætter)
for vores data vil den forudsigelige relation blive udtrykt som:
pris = – $9,590,000 + $2,552 * boligareal + 3,202,000 * bade-791
* boligareal * bade
dette giver et mål ejendom forudsigelse af $577,523, som har en fejl på $29,477 ($607,000 – $577,523 = $29,477) og en relativ fejl på 5 procent, hvilket er den bedste pasform hidtil!
Hvornår skal man bruge Simple vs. Multipel lineær Regression
ved vurdering af en ejendom eller bestemmelse af værdien af en bestemt funktion kan bedømmere bruge regressionsanalyse til at udlede de mest nøjagtige prisjusteringer ved at tage højde for effekten af flere funktioner på en ejendoms værdi. Nye brancheregler, der kræver datadrevet begrundelse for vurderingsbeslutninger, kan gøre regressionsanalyse endnu mere nødvendig for bedømmere i den nærmeste fremtid.
Husk, at det måske ikke altid er muligt at bruge en multipel lineær regressionsanalyse. Hvis der for eksempel ikke er et varieret udvalg af datapunkter til rådighed for en ejendom og dens sammenligninger, er der muligvis ikke nok information til at foretage en MLR-analyse. Men når der er nok tilgængelige data til at udføre en MLR-analyse, producerer det ofte de mest nøjagtige resultater. Husk, at der er tidspunkter, hvor en MLR-analyse kræver et yderligere udtryk, der repræsenterer forudsigernes interaktion for at være mest nøjagtige, såsom i eksemplet ovenfor. Mens regressionsanalyse klart ikke erstatter en taksators ekspertise-kan det være et værdifuldt supplement til det.
vi håber du vil finde disse indsigter nyttige til dine vurderinger.
> CE Online – 7 timer (godkendt i 40 stater)
sådan understøtter og beviser du dine justeringer
præsenteret af: Richard Hagar, SRA
skal kende forretningspraksis for alle bedømmere, der arbejder i dag. Sørg for korrekt støtte til dine justeringer. At foretage forsvarlige justeringer er det første skridt i at blive en “Tier One” taksator, der tjener mere, nyder de bedste opgaver og lider færre ulemper og tilbagekald. Op dit spil, undgå tidskrævende tilbagekald og tjen godkendt CE i dag! Tilmeld Dig Nu! $119 (7 timer)
OREP Insured ‘ s Price: $99
om forfatteren
Dr. Keying ye er Professor i statistik ved College of Business i University of San Antonio og også seniorforsker ved HouseCanary, hvor han udvikler forudsigelig analyse til dets førende vurderingsprogram, HouseCanary Appraiser og andre produkter. HouseCanary taksator hjælper bolig bedømmere lukke mere forretning gennem en nem at bruge løsning og omfatter former som 1004, 2055, 1075, og mere!
