
 |
tjänster som erbjuds denna fråga
> värderingsman Coach |
Redaktörens anmärkning: Den här historien finns i den nya utgåvan av Working RE (just postad). Är jag en fungerande Re abonnent? OREP e& O försäkrade har en gratis prenumeration.
Hur Mycket Värde Lägger Det Extra Sovrummet Till? (Förstå Regression)
av Dr.Keying Ye
i de enklaste termerna utvärderar Fastighetsvärderare det verkliga marknadsvärdet för en fastighet — ett nummer som aggregerar värdet av ett brett utbud av fastighetens funktioner, både kvantitativa (antal sovrum och badrum, kvadratmeter, partistorlek, antal garage etc.) och kvalitativa (vyer, gatuscen, plats, etc.). Eller hur?
ett sätt att approximera detta värde är att använda regressionsmetoden, som är ett dataanalysverktyg för att studera förhållandet mellan en beroende variabel (i detta fall fastighetsvärde) och funktionsprognoser (t.ex. antal badrum eller bruttobostadsyta). Denna artikel syftar till att visa hur regression kan öka bedömningsnoggrannheten genom att fokusera på de två vanligaste typerna: enkel vs multipel linjär Regression.
hantera enkel linjär Regression
enkel linjär regression (SLR) är en enkel regressionsmetod med endast en prediktor och en beroende variabel. Om vi till exempel tror att vi kan använda bostadsområdet som den enda prediktorn för att uppskatta en fastighets värde och att sambandet mellan bostadsområdet och värdet på en fastighet är linjärt relaterat, kan vi använda en enkel linjär regression för att uppskatta värdet.
en prediktiv struktur av SLR kan uttryckas som prediction = m + b * funktion.
i det här fallet är funktionen den oberoende variabeln och förutsägelsen är svarvariabeln (tänk tillbaka till y = m + bx från high school algebra). Här är” m” och ”b” ”lutningen” respektive ”avlyssning” av en graf gjord av denna ekvation. Avlyssningen är där förutsägelsen skulle vara om funktionen är noll (om ämnesegenskapen inte har ett garage till exempel). Lutningen är ökningen eller minskningen av fastighetsvärdet för varje enhetsändring i funktionen (t.ex. hur mycket fastighetens värde ändras för varje kvadratfot som läggs till eller subtraheras).
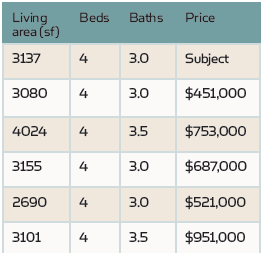
Tänk på följande exempel. Vi vill förutse värdet av en singlefamily residence (SFR) och vi vet dess grundläggande information som vardagsrum, antal sängar och antal bad. Med hjälp av HouseCanary ’ s pre-computed comps-analys identifierar vi de fem mest liknande fastigheterna som sålts under de senaste sex månaderna, som visas i tabellen nedan.
(Berättelsen fortsätter nedan)
(Berättelsen fortsätter)
likheten bestäms av egenskapstyper (SFR eller andra), egenskapsfunktioner och de geografiska avstånden mellan dessa egenskaper och ämnesegenskapen. Eftersom varje fastighet har samma antal sovrum, har denna funktion ingen inverkan på priset bland dessa egenskaper än som en fast konstant. Prisvariationen är dock tydligt förknippad med vardagsrum och antalet bad.
siffrorna nedan visar förhållandet mellan fastighetspriserna och antingen vardagsrummet eller antalet bad för var och en av fastigheterna (se tomter 1 och 2). I varje diagram visar punkten där den vertikala bruna linjen berör den horisontella axeln ämnesegenskapens värde för funktionen i fråga (3 137 för vardagsrum och 3,0 för badrum). Den blå linjen är den linjära regressionslinjen med en prediktor, som visar det prediktiva förhållandet mellan fastighetspriset och lämplig funktion.
(Berättelsen fortsätter nedan)
(Berättelsen fortsätter)
i plot 1 uttrycks till exempel prognosförhållandet mellan pris och bostadsyta som: pris =200 323 + 147 * bostadsyta. För ämnesfastigheten, som mäter 3,137 kvadratmeter, betyder det att det förutspådda priset är $661,462: $661,462 = ($200,323 + $147 * 3137) detta visas som den fasta blå pricken i diagrammet 1. Regressionslinjens ”lutning”, 147, mäter prisvärdet per enhet, dvs prisjusteringen för varje ytterligare kvadratmeter (plot 1). Men om vi använder antal badrum som vår prediktor istället är målegendomens förutsagda pris $553,000 (-$1,241,000 + $598,000 * 3.0 = $553,000). Denna skillnad i förutsagt pris ($661,462 och $553,000) är vanligt när man använder enkla linjära regressionsformler för olika funktioner i samma egenskap (se diagram 2 diagram ovan).
det faktiska priset för målegenskapen är $607 000, vilket visas som en brun stjärna i varje graf. Följaktligen, felen för båda uppskattningarna är nästan identiska, om än i motsatt riktning, oavsett om de uttrycks i råa Dollar ($607,000 – $661,462 = -$54,462 och $607 000 – $553 000 = $ 54 000 respektive) eller i procent (-$54,462/$607,000 = – 9 procent och $54,000 / $607,000 = 9 procent, respektive).
gå vidare med multipel linjär Regression
med enkel linjär regression kan en bedömare använda den viktigaste prediktorn för en fastighets värde för att göra sin bedömningsanalys (eller till och med använda SLR-analys på flera funktioner för att få flera referenspunkter. Men vad händer om den viktigaste prediktorn inte är klar? Vad händer om, till exempel, alla tre sovrum enheter i en given analys har ett annat antal badrum, varierande brutto vardagsrum, eller bara ett par av dem har pooler? Genom att använda multiple linear regression (MLR) kan bedömare jämföra effekten som flera prediktorer har på ett fastighetsvärde med en enda beräkning.
en prediktiv struktur av MLR kan uttryckas som:
prediction = m + b1 * funktion 1 + b2 * funktion 2 + b3 * funktion 3+ …
till exempel med uppgifterna ovan kan vi regressera priset med både vardagsrum och antal badrum: pris = -$1,309,770 – $125 * vardagsrum + $744,918 * bad.
om vi kopplar in målegenskapens funktionsvärden är det förutsagda priset $532,859, vilket ger ett fel på $74,141 eller 12%. Felet i denna förutsägelse är värre än de fel som beaktas i SLR, men oroa dig inte, det finns en förklaring i data (och en lösning som följer!).
först måste vi överväga relationerna mellan prediktorerna själva och förstå vilken information bokstäverna i ekvationen ovan förmedlar, vilket inte är så enkelt i det här fallet som det var när man använde SLR. Till exempel, koefficienten -$125 för vardagsrummet säger att, för ett fast antal bad, ökar vardagsrummet med en kvadratmeter faktiskt fastighetspriset med $125 — vilket verkar onaturligt! Men om vi tittar på tabellen ovan kan vi se att för 3,5 badrum finns detbara två egenskaper. Den med 3,101 kvadratmeter är faktiskt dyrare ($951,000) än fastigheten med 4,024 kvadratmeter. För de tre fastigheterna med 3,0 badrum korrelerar inte vardagsrummen (2690, 3080, 3155) exakt med priserna ($521,000, $451,000, $687,000) antingen.
(Berättelsen fortsätter nedan)

(Berättelsen fortsätter)
detta innebär att vi i våra data har ett annat linjärt förhållande mellan svarspriset och prediktorns vardagsrum för fastigheterna med ett annat antal badrum. I nästa diagram nedan visar den svarta linjen (regressionslinjen med bad = 3,0) och den röda linjen (regressionslinjen med bad = 3,5) faktiskt motsatta trender. I ett sådant fall är båda prediktorerna inte rent additiva mot priset-en ökning med eninnebär inte omedelbart en ökning av priset. Åtgärden till detta är att lägga till en annan term, vardagsrum * antal bad, vilket representerar interaktionen mellan prediktorerna.
(Berättelsen fortsätter nedan)
(Berättelsen fortsätter)
för våra data skulle det prediktiva förhållandet uttryckas som:
pris = – $9,590,000 + $2,552 * vardagsrum + 3,202,000 * bad-791
* vardagsrum * bad
detta ger en målegendomsprognos på $577,523, vilket har ett fel på $29,477 ($607,000 – $577,523 = $29,477) och ett relativt fel på 5 procent, vilket är den bästa passformen hittills!
när du ska använda Simple vs. Multipel linjär Regression
vid bedömning av en fastighet eller bestämning av värdet på en viss funktion kan bedömare använda regressionsanalys för att härleda de mest exakta prisjusteringarna genom att ta hänsyn till effekten av flera funktioner på en fastighets värde. Nya branschregler som kräver datadriven motivering för bedömningsbeslut kan göra regressionsanalys ännu mer nödvändig för bedömare inom en snar framtid.
Tänk på att det kanske inte alltid är möjligt att använda en multipel linjär regressionsanalys. Om det till exempel inte finns ett varierat utbud av datapunkter tillgängliga för en fastighet och dess jämförbara, kanske det inte finns tillräckligt med information för att genomföra en MLR-analys. Men när det finns tillräckligt med tillgängliga data för att utföra en MLR-analys, ger det ofta de mest exakta resultaten. Kom ihåg att det finns tillfällen då en MLR-analys kräver en ytterligare term som representerar interaktionen mellan prediktorerna för att vara mest exakt, till exempel i exemplet ovan. Medan regressionsanalys helt klart inte ersätter en bedömares expertis-det kan vara ett värdefullt komplement till det.
vi hoppas att du hittar dessa insikter användbara för dina bedömningar.
> CE Online-7 timmar (godkänd i 40 stater)
hur man stöder och bevisar dina justeringar
Presenterad av: Richard Hagar, SRA
måste-veta affärsmetoder för alla bedömare som arbetar idag. Se till att du har rätt stöd för dina justeringar. Att göra försvarbara justeringar är det första steget i att bli en ”Tier One” värderingsman, som tjänar mer, har de bästa uppdragen och lider färre hakar och återuppringningar. Upp ditt spel, undvika tidskrävande återuppringningar och tjäna godkänd CE idag! Registrera Dig Nu! $119 (7 timmar)
OREP försäkrade Pris: $99
om författaren
Dr.Keying Ye är Professor i statistik vid College of Business i University of Texas i San Antonio och även en Senior forskare vid HouseCanary där han utvecklar prediktiv analys för sin ledande bedömning programvara, HouseCanary värderingsman och andra produkter. HouseCanary Appraiser hjälper bostadsvärderare att stänga fler affärer genom en lättanvänd lösning och innehåller formulär som 1004, 2055, 1075 och mer!
