o levantamento é uma etapa preliminar essencial para qualquer trabalho de construção.
todo o plano do local determina a estrutura de um edifício ou local. Temos vários métodos de levantamento para entender a natureza de um enredo.
- Cadeia de Topografia
- Avião Tabela de Topografia
- Bússola de Topografia
- Topográfico, Levantamento, etc
Tudo o que ele faz é gravar as medidas reais em um papel para facilitar o cálculo de área. Mas como calcular a área do enredo?
como calcular a área da parcela?
a área nada mais é do que um espaço ocupado por qualquer forma geométrica. Para cálculos básicos de área, poderíamos usar as fórmulas abaixo.
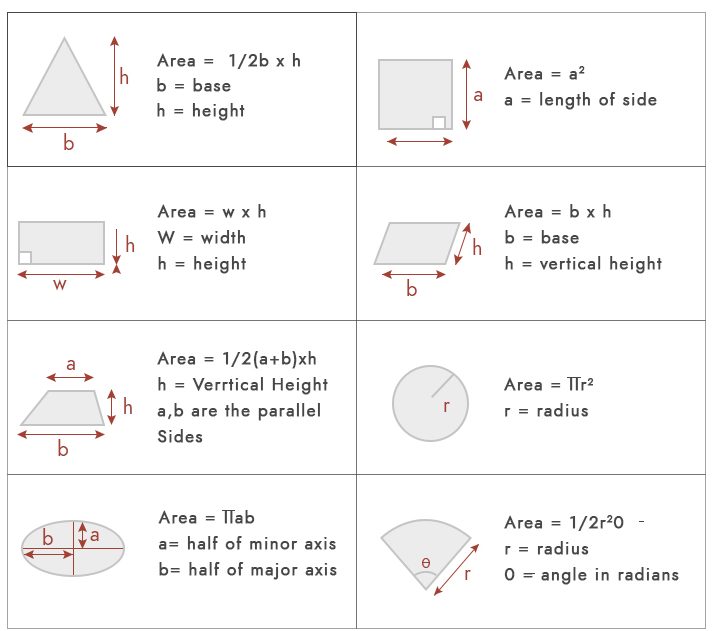
mas, em termos práticos, a maior parte da trama não se enquadra nessas formas geométricas. Tipos mais comuns de enredo áreas são
- Triangular Enredo
- Polígonos Irregulares
- Quadrado ou Retangular
Para ilustrar as fórmulas, supondo que temos diferentes formas de parcelas.
triângulo plot
supondo que temos um triângulo de 40 pés de base & largura.
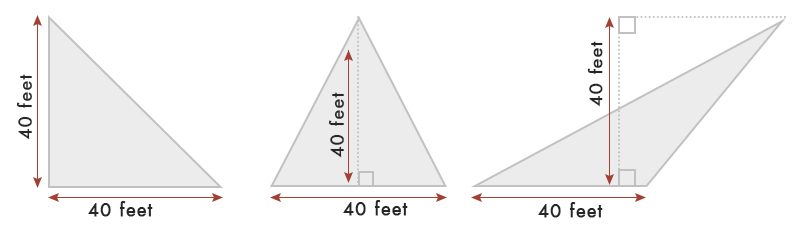
de acordo com a tabela, a Área do triângulo = ½ x base x largura = ½ x 40 x 40 = 80 metros Quadrados.pés
Se você não pode ser capaz de medir a altura do triângulo e, se não for um ângulo reto, em seguida, você pode usar a fórmula abaixo
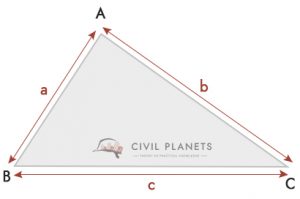
![]()
Onde S = Perímetro do triângulo = (a + b + c)/2
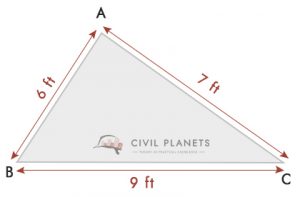
a Partir do desenho, a = 6 pés, b = 9 pés & c = 7 pés, S = (6+9+7)/2 = 11
Portanto, Área do terreno = √S(S-a)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft 2 21 Sq.ft
polígonos irregulares
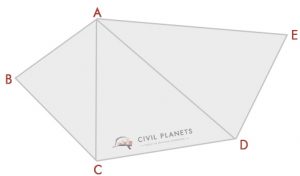
a maioria de nós poderia reconhecer esse tipo de enredo. Para encontrar a área dessa forma, temos que usar o cálculo da trigonometria. Não é assim tão difícil.
Vamos encontrar a área desta forma, em dois casos típicos
- Polígonos Irregulares (com conhecidos intersecção dimensões)
- Polígonos Irregulares (com ângulos)
Polígonos Irregulares (com conhecidos intersecção dimensões)
Imaginar, temos o seguinte gráfico, com o conhecido intersecção dimensões.
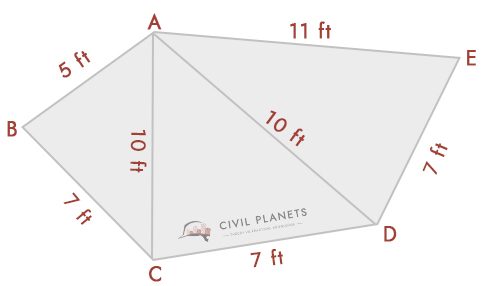
usando a fórmula triangular acima, podemos resolver isso. A partir do diagrama, temos três nomeadamente triângulos ABC, ACD, & ADE
- Triângulo 1 – Δ ABC, Onde S = (5+7+10)/2 = 11
Fórmula para Área = √S(S-a)(S-b)(S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Triângulo 2 – ∆ ACD, Onde S = (10+7+10)/2 = 13.5
Fórmula para Área = √S(S-a)(S-b)(S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Triângulo 3 – Δ ADE, Onde S = (10+7+11)/2 = 14
Fórmula para Área = √S(S-a)(S-b)(S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
área total da forma = 16.25+32.79+34.29 = 83,33 Sq.ft
Polígonos Irregulares (com ângulos)
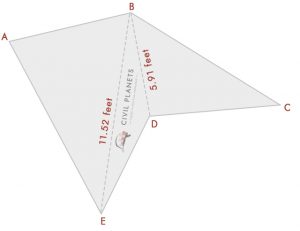
Supondo agora nós não sabemos o cruzamento de medição de só ter ângulos, como abaixo pic
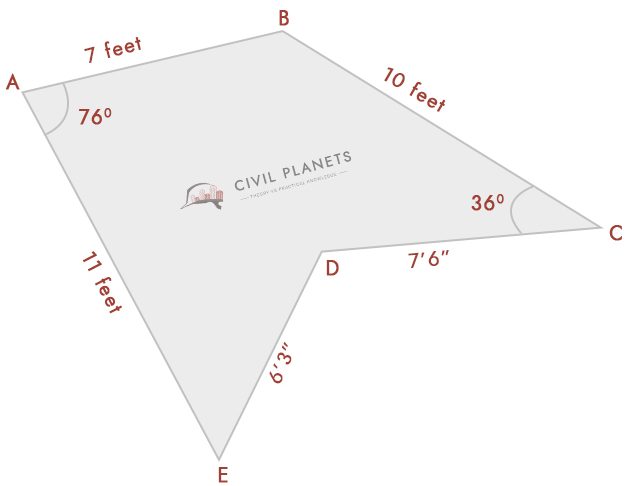
Agora separe a imagem acima em três triângulos abaixo
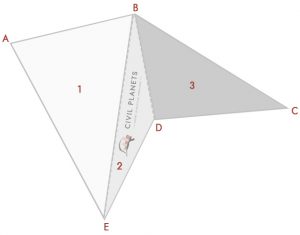
Agora temos 3 triângulos assim como os acima, única coisa em vez de intersecção dimensão; temos ângulos. Então, a primeira coisa é que temos que calcular a medição de interseção usando trigonometria.
intersecção de medição pode ser obtido por Heron fórmula c2 = a2 + b2 – 2abCos(C)
Onde, a = comprimento de AB, b = comprimento da AE, c = comprimento da EB
Duração do EB = √(a2 + b2 – 2abCos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 pés
Duração do DB = √(a2 + b2 – 2abCos(C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 pés
Agora sabemos que o comprimento de cada lado, utilizando-se o triângulo fórmula, podemos calcular a área agora
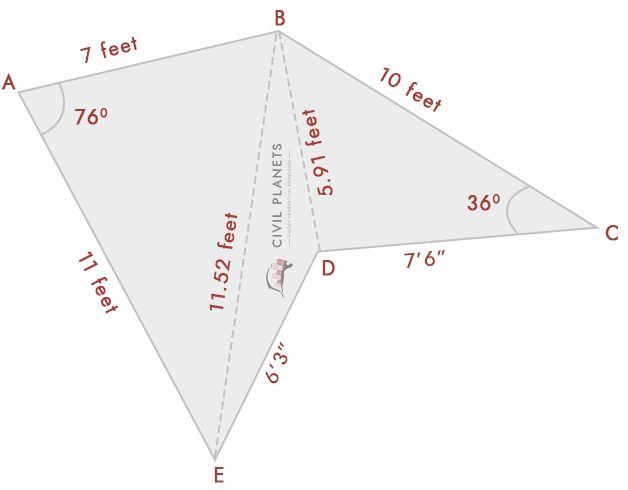
a Partir do diagrama, temos três triângulos
Triângulo 1 – Δ ABE, Onde S = (7+11+11.52)/2 = 14.76
Fórmula para Área = √S(S-a)(S-b)(S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
Triângulo 2 – Δ CAMA, Onde S = (11.52+6.25+5.91)/2 = 11.84
Fórmula para Área = √S(S-a)(S-b)(S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
Triângulo 3 – ∆ BDC, Onde S = (5.91+7.5+10)/2 = 11.70
Fórmula para Área = √S(S-a)(S-b)(S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
área total da forma = 37.35+11.21+21.99 = 70,55 m2.ft
aprendizagem feliz 🙂
