Oppmåling er et viktig foreløpig skritt for ethvert byggearbeid.
hele områdeplanen bestemmer strukturen til en bygning eller et område. Vi har mange metoder for oppmåling for å forstå naturen til et tomt.
- Kjedeoppmåling
- Planetabelloppmåling
- Kompassoppmåling
- Topografisk Oppmåling etc
alt det gjør er å registrere de faktiske målingene i et papir for enkel beregning av areal. Men hvordan å beregne tomten området?
Hvordan Beregne Tomteområdet?
området er ikke noe annet enn et rom okkupert av noen geometrisk form. For grunnleggende områdeberegninger kan vi bruke formlene nedenfor.
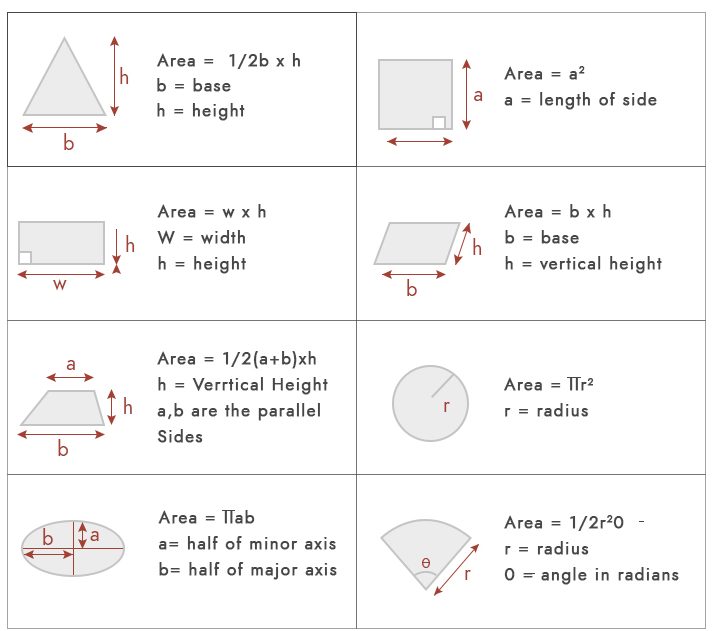
men i praksis faller det meste av plottet ikke under disse geometriske former. De vanligste typene plottområder er
- Trekantet Plott
- Uregelmessige Polygoner
- Kvadratiske Eller Rektangulære
for å illustrere formlene, forutsatt at vi har forskjellige former for plott.
Triangle plot
Forutsatt at vi har en trekant på 40 fot base & bredde .
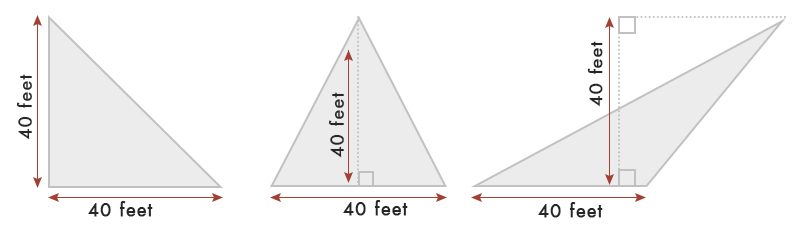
I henhold til tabellen Er arealet av trekanten = hryvnias x base x bredde = hryvnias x 40 x 40 = 80 Kvm.ft
hvis du ikke kan måle høyden på trekanten, og hvis den ikke er en rett vinkel, kan du bruke formelen nedenfor
![]()
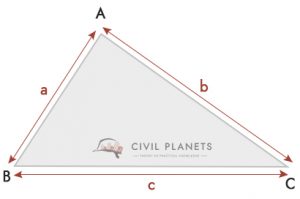
Hvor S = Perimeter av trekant = (a + b + c)/2
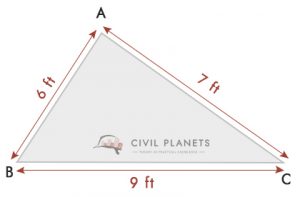
fra tegningen, a = 6 fot, b = 9 fot & c = 7 fot, S = (6+9+7)/2 = 11
Derfor Er Arealet av tomten = √S(S-a)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft ≅ 21 Sq.ft
Uregelmessige Polygoner
De fleste av oss kunne gjenkjenne denne typen tomt. For å finne området i denne formen må vi bruke trigonometri beregning. Det er ikke så vanskelig.
La oss finne området i denne formen i to typiske tilfeller
- Uregelmessige Polygoner (med kjente skjæringsdimensjoner)
- Uregelmessige Polygoner (med vinkler)
Uregelmessige Polygoner (med kjente skjæringsdimensjoner)
Tenk deg at vi har følgende plott, med kjente skjæringsdimensjoner.
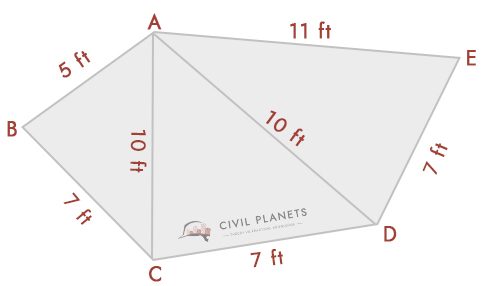
Ved å Bruke den trekantede formelen ovenfor kan vi løse dette. Fra diagrammet har vi tre trekanter nemlig ABC, ACD, & ADE
- Trekant 1-Δ ABC, Hvor S = (5+7+10)/2 = 11
Formel For Areal = √S(S-a)(S-b)(S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Trekant 2-Δ ACD, Hvor S = (10+7+10)/2 = 13.5
Formel For Areal = √S(S-a)(S-b)(S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Trekant 3-Δ ADE, Hvor S = (10+7+11)/2 = 14
Formel For Areal = √S(S-a)(S-b)(S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
så totalt areal av formen = 16.25+32.79+34.29 = 83,33 Kvm.ft
Uregelmessige Polygoner (med vinkler)
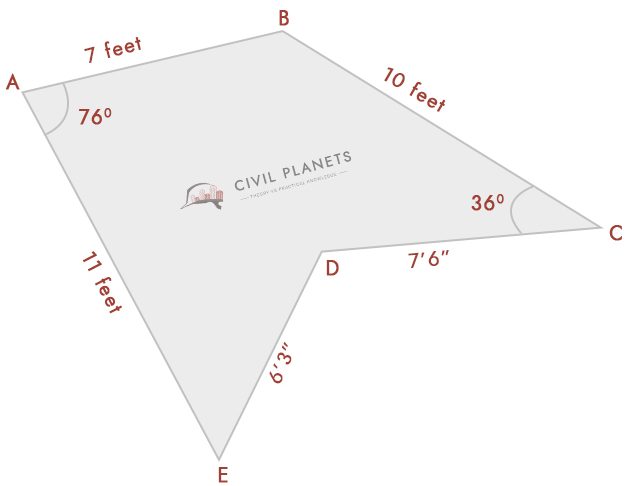
Antar nå vet vi ikke skjæringsmålingen bare med vinkler som under pic
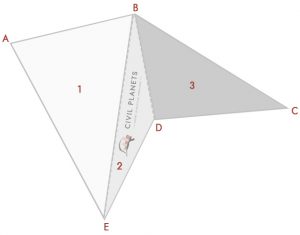
nå skille bildet over i tre trekanter som nedenfor
Nå har vi 3 trekanter akkurat som ovenfor, bare ting i stedet for skjæringsdimensjonen; vi har vinkler. Så det første er at vi må beregne skjæringsmålingen ved hjelp av trigonometri.
skjæringsmålingen kan oppnås med Herons formel c2 = a2 + b2 – 2abCos (C)
hvor, a = LENGDE PÅ AB, b = LENGDE PÅ AE, c = LENGDE PÅ EB
LENGDE PÅ EB = √(a2 + b2-2abCos(C))
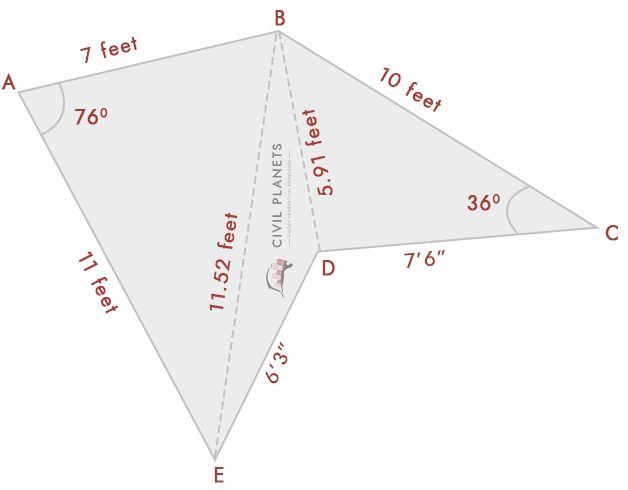
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 føtter
LENGDE PÅ DB = √(a2 + b2-2abcos(C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 føtter
nå vet vi lengden på hver side, ved hjelp av trekantformelen, kan vi beregne området nå
fra diagrammet har vi tre trekanter
Trekant 1-Δ ABE, Hvor S = (7+11+11.52)/2 = 14.76
Formel For Areal = √S(S-a)(S-b)(S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
Trekant 2-Δ SENG, Hvor S = (11.52+6.25+5.91)/2 = 11.84
Formel For Areal = √S(S-a)(S-b)(S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
Trekant 3-Δ BDC, Hvor S = (5.91+7.5+10)/2 = 11.70
Formel For Areal = √S(S-a)(S-b)(S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
så totalt areal av formen = 37.35+11.21+21.99 = 70,55 Kvm.ft
Glad Læring 🙂
