Il rilevamento è un passo preliminare essenziale per qualsiasi lavoro di costruzione.
L’intero piano del sito determina la struttura di un edificio o di un sito. Abbiamo numerosi metodi di rilevamento per comprendere la natura di una trama.
- Topografia a catena
- Topografia a tavola piana
- Topografia a bussola
- Topografia topografica ecc
Tutto ciò che fa è registrare le misurazioni effettive in una carta per un facile calcolo dell’area. Ma come calcolare l’area della trama?
Come calcolare l’area della trama?
L’area non è altro che uno spazio occupato da qualsiasi forma geometrica. Per i calcoli di base dell’area, potremmo usare le formule seguenti.
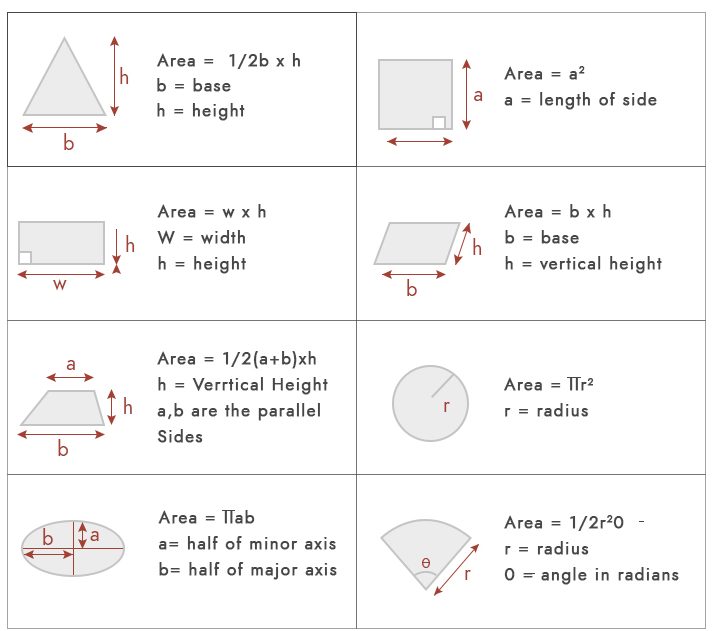
Ma in termini pratici, la maggior parte della trama non rientra in queste forme geometriche. I tipi più comuni di aree di trama sono
- Trama triangolare
- Poligoni irregolari
- Quadrato o rettangolare
Per illustrare le formule, supponendo che abbiamo diverse forme di trame.
Triangolo plot
Supponendo che abbiamo un triangolo di 40 piedi base & larghezza.
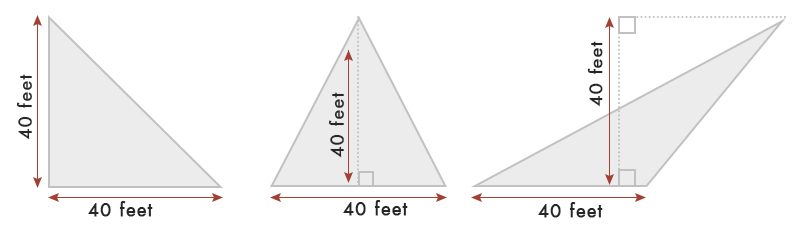
Come da tabella, Area del triangolo = ½ x base x larghezza = ½ x 40 x 40 = 80 Sq.ft
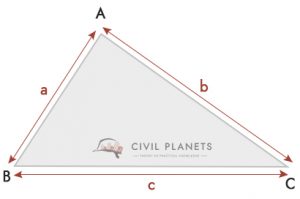
Se non si può essere in grado di misurare l’altezza del triangolo e se non è un angolo retto, quindi si potrebbe usare la formula qui di seguito
![]()
Dove S = Perimetro del triangolo = (a + b + c)/2
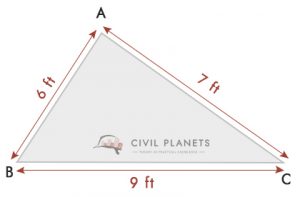
Dal disegno, a = 6 piedi, b = 9 piedi & c = 7 metri, S = (6+9+7)/2 = 11
Pertanto, Area del terreno = √S(S-a)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft Sq 21 Mq.ft
Poligoni irregolari
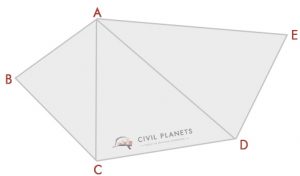
La maggior parte di noi potrebbe riconoscere questo tipo di trama. Per trovare l’area di questa forma, dobbiamo usare il calcolo della trigonometria. Non è così difficile.
andiamo a trovare la zona di questa forma in due casi tipici
- Poligoni Irregolari (con nota di intersezione dimensioni)
- Poligoni Irregolari (con angoli)
Poligoni Irregolari (con nota di intersezione dimensioni)
supponiamo di avere la seguente trama, con nota di intersezione dimensioni.
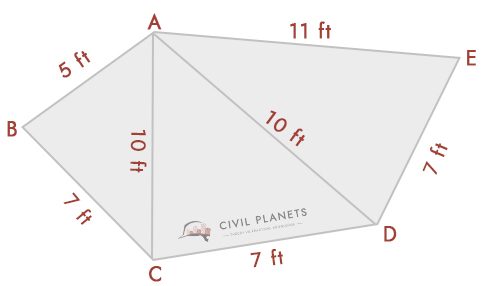
Usando la formula triangolare sopra, possiamo risolvere questo. Dal diagramma, abbiamo tre triangoli cioè ABC, ACD,& ADE
- Triangolo 1-Δ ABC, Dove S = (5+7+10)/2 = 11
Formula per Area = √S (S-a)(S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Triangolo 2-Δ ACD, Dove S = (10+7+10)/2 = 13.5
Formula per Area = √S (S-a)(S-b) (S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Triangolo 3-Δ ADE, Dove S = (10+7+11)/2 = 14
Formula per Area = √S (S-a)(S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
Così superficie totale della forma = 16.25+32.79+34.29 = 83,33 Sq.ft
Poligoni Irregolari (con angoli)
Supponendo che ormai non sappiamo l’intersezione di misura solo con gli angoli come di seguito pic
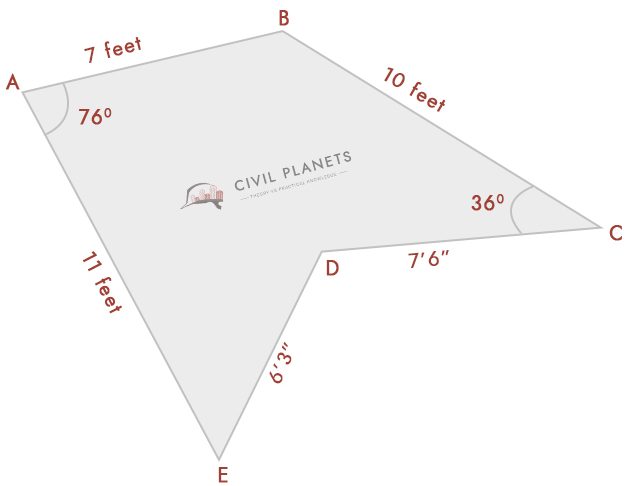
Ora separata di cui sopra l’immagine in tre triangoli, come di seguito
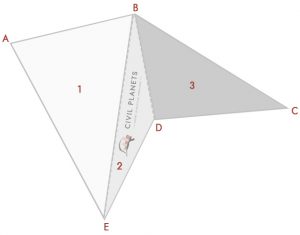
Ora abbiamo 3 triangoli come sopra, unica cosa, invece di intersezione dimensione; abbiamo angolazioni. Quindi la prima cosa è che dobbiamo calcolare la misura dell’intersezione usando la trigonometria.
L’intersezione di misura può essere ottenuta dalla formula di erone c2 = a2 + b2 – 2abCos(C)
Dove, a = lunghezza di AB, b = lunghezza di AE, c = lunghezza di EB
Lunghezza di EB = √(a2 + b2 – 2abCos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 piedi
Lunghezza del DB = √(a2 + b2 – 2abCos(C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 metri
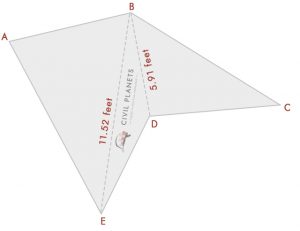
Ora sappiamo che la lunghezza di ogni lato, con il triangolo formula, possiamo calcolare l’area ora
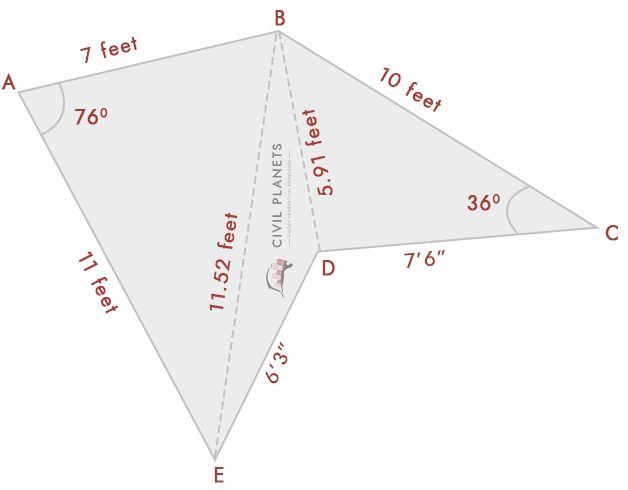
Dal grafico, abbiamo tre triangoli
Triangolo 1 – Δ ABE, Dove S = (7+11+11.52)/2 = 14.76
Formula Area = √S(S-a)(S-b)(S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
Triangolo 2-Δ LETTO, Dove S = (11.52+6.25+5.91)/2 = 11.84
Formula per Area = √S (S-a)(S-b) (S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
Triangolo 3-Δ BDC, Dove S = (5.91+7.5+10)/2 = 11.70
Formula per Area = √S (S-a)(S-b) (S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
Così superficie totale della forma = 37.35+11.21+21.99 = 70,55 mq.ft
Apprendimento felice 🙂
