
 |
szolgáltatások felajánlotta ezt a kérdést
> az értékbecslő edző |
a szerkesztő megjegyzése: Ez a történet megtalálható a Working RE új nyomtatott kiadásában (csak postázva). Vagyok egy működő újra Előfizető? OREP e& O a biztosítottak ingyenes előfizetést élveznek.
Mennyi Értéket Ad Az Extra Hálószoba? (Understanding regresszió)
Dr. Keying Ye
a legegyszerűbb értelemben az ingatlanértékelők értékelik az ingatlan valós piaci értékét — egy számot, amely összesíti az ingatlan jellemzőinek széles skáláját, mind mennyiségi (hálószobák és Fürdőszobák száma, alapterület, telekméret, garázsok száma stb.) és minőségi (nézetek, utcai jelenet, helyszín stb.). Igaz?
ennek az értéknek a közelítésének egyik módja a regressziós módszer, amely egy adatelemző eszköz a függő változó (ebben az esetben a tulajdonságérték) és a jellemző prediktorok (például a Fürdőszobák száma vagy a bruttó lakóterület) közötti kapcsolat tanulmányozására. Ez a cikk célja annak bemutatása, hogy a regresszió hogyan növelheti az értékelési pontosságot a két leggyakoribb típusra összpontosítva: egyszerű vs.többszörös lineáris regresszió.
az egyszerű lineáris regresszió kezelése
az egyszerű lineáris regresszió (SLR) egy egyszerű regressziós megközelítés, amely csak egy prediktort és egy függő változót használ. Például, ha úgy gondoljuk, hogy a lakóterületet használhatjuk egyetlen előrejelzőként egy ingatlan értékének becsléséhez, és hogy a lakóterület és az ingatlan értéke közötti kapcsolat lineárisan kapcsolódik, akkor egyszerű lineáris regressziót használhatunk az érték becsléséhez.
a tükörreflexes fényképezőgép prediktív szerkezete kifejezhető predikció = m + b * funkcióként.
ebben az esetben a feature a független változó, a predikció pedig a válaszváltozó (gondoljon vissza y = m + bx-re a középiskolai algebrából). Itt az” m “és a” b “az ebből az egyenletből készült gráf” meredeksége”, illetve” metszete”. A lehallgatás az, ahol a jóslat lenne, ha a jellemző nulla (ha a tárgy tulajdonság nem rendelkezik garázs például). A meredekség a tulajdonság értékének növekedése vagy csökkenése a jellemző minden egyes egységváltozása esetén (például az, hogy az ingatlan értéke mennyiben változik minden hozzáadott vagy kivont négyzetláb után).
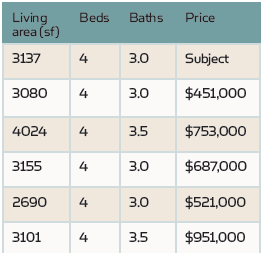
Tekintsük a következő példát. Szeretnénk előre jelezni az egycsaládos rezidencia (SFR) értékét, és ismerjük az alapvető információkat, például a lakóterületet, az ágyak számát és a fürdők számát. A HouseCanary előre kiszámított comps elemzésével azonosítjuk az elmúlt hat hónapban eladott öt leginkább hasonló ingatlant, amint az az alábbi táblázatban látható.
(a történet alább folytatódik)
(
a hasonlóságot a tulajdonságtípusok (SFR vagy mások), a tulajdonság jellemzői, valamint a tulajdonságok és a tárgy tulajdonság közötti földrajzi távolság határozza meg. Mivel minden ingatlan azonos számú hálószobával rendelkezik, ez a funkció nincs hatással az árra ezen tulajdonságok között, csak rögzített állandóként. Az árváltozás azonban egyértelműen összefügg a lakóterülettel és a fürdők számával.
az alábbi ábrák az ingatlanárak és az egyes ingatlanok lakóterülete vagy fürdőinek száma közötti kapcsolatot mutatják (Lásd az 1.és 2. parcellát). Minden grafikonon az a pont, ahol a függőleges barna vonal érinti a vízszintes tengelyt, megmutatja a tárgy tulajdonság értékét a kérdéses jellemzőre (3,137 a lakóterületre és 3,0 a fürdőszobákra). A kék vonal az egy prediktoros lineáris regressziós vonal, amely az ingatlanár és a megfelelő tulajdonság közötti prediktív kapcsolatot mutatja.
(a történet alább folytatódik)
(
az 1. ábrán például az ár és a lakóterület közötti előrejelzési kapcsolat a következőképpen fejeződik ki: ár =200 323 + 147 * lakóterület. A tárgy tulajdonság, amely intézkedések 3,137 négyzetméter, ez azt jelenti, hogy a várható ár $661,462: $661,462 = ($200,323 + $147 * 3137) ez látható, mint a szilárd kék pont a plot 1 grafikon. A 147 regressziós egyenes “meredeksége” az egységár értékét, azaz az egyes további négyzetlábak árkorrekcióját méri (1.ábra). Ha azonban a fürdőszobák számát használjuk előrejelzőként, akkor a céltulajdon előre jelzett ára az $553,000 (-$1,241,000 + $598,000 * 3.0 = $553,000). Ez az eltérés az előre jelzett árban ($661,462 és $553,000) gyakori, ha egyszerű lineáris regressziós képleteket használunk ugyanazon tulajdonság különböző jellemzőire (lásd a fenti 2.ábrát).
a céltulajdonság tényleges ára 607 000 USD, amely minden grafikonon barna csillagként jelenik meg. Következésképpen, mindkét becslés hibái közel azonosak, bár az ellenkező irányba, akár nyers dollárban kifejezve($607,000 – $661,462 = -$54,462 607 000-553 000 USD = 54 000 USD) vagy százalékban (-$54,462/$607,000 = – 9 százalék és $54,000 / $607,000 = 9 százalék).
tovább haladva többszörös lineáris regresszióval
egyszerű lineáris regresszióval az értékbecslő az ingatlan értékének legfontosabb előrejelzőjével elvégezheti értékelési elemzését (vagy akár tükörreflexes elemzést is használhat több funkción, hogy több referenciapontot kapjon. De mi van, ha a legfontosabb előrejelző nem egyértelmű? Mi van, ha például egy adott elemzés mind a három hálószobás egységében eltérő számú fürdőszoba van, változó bruttó lakóterület, vagy csak néhányuknak van medencéje? A többszörös lineáris regresszió (MLR) alkalmazásával az értékelők egyetlen számítással összehasonlíthatják azt a hatást, amelyet több prediktor gyakorol az ingatlan értékére.
az MLR prediktív szerkezete a következőképpen fejezhető ki:
előrejelzés = m + b1 * 1. funkció + b2 * 2. funkció + b3 * 3. funkció + …
például a fenti adatokkal mind a nappali, mind a Fürdőszobák száma szerint vissza tudjuk állítani az árat: ár = – 1 309 770 USD – 125 USD * nappali + 744 918 USD * fürdők.
ha csatlakoztatjuk a céltulajdonság jellemző értékeit, az előre jelzett ár 532 859 USD, ami 74 141 USD vagy 12% hibát eredményez. Ennek az előrejelzésnek a hibája rosszabb, mint a tükörreflexes fényképezőgépekben figyelembe vett hibák, de ne aggódjon, van magyarázat az adatokban (és az ezt követő megoldás!).
először is meg kell vizsgálnunk a prediktorok közötti kapcsolatokat, és meg kell értenünk, hogy a fenti egyenlet betűi milyen információkat közvetítenek, ami ebben az esetben nem olyan egyszerű, mint az SLR használatakor. Például, az együttható – $125 a nappali azt mondja, hogy egy meghatározott számú fürdők, növekvő nappali egy négyzetméterrel valójában csökkenti az ingatlan ára $125-ami úgy tűnik, természetellenes! Ha azonban megnézzük a fenti táblázatot, láthatjuk, hogy 3,5 fürdőszoba esetében vancsak két tulajdonság. A 3101 négyzetméteres valójában drágább (951 000 dollár), mint a 4024 négyzetméteres ingatlan. A 3,0 fürdőszobával rendelkező három ingatlan esetében a lakóterületek (2690, 3080, 3155) nem korrelálnak pontosan az árakkal ($521,000, $451,000, $687,000) egyik sem.
(a történet alább folytatódik)

(
ez azt jelenti, hogy adatainkban eltérő lineáris kapcsolat áll fenn a válaszár és a prediktor lakóterület között az eltérő számú fürdőszobával rendelkező ingatlanok esetében. Így az alábbi következő grafikonon a fekete vonal (a regressziós vonal baths = 3,0) és a piros vonal (a regressziós vonal baths = 3,5) valójában ellentétes tendenciákat mutat. Ebben az esetben mindkét előrejelző nem pusztán adalékanyag az árhoz képest—egy növekedésnem jelenti azonnal az áremelkedést. Ennek orvoslása egy másik kifejezés hozzáadása, Nappali * fürdők száma, amely a prediktorok kölcsönhatását képviseli.
(a történet alább folytatódik)
(
adataink esetében a prediktív összefüggést a következőképpen fejezzük ki:
ár = – $9,590,000 + $2,552 * nappali + 3,202,000 * fürdők-791
* Nappali * fürdők
ez 577,523 dolláros céltulajdonság-előrejelzést eredményez, amelynek hibája $29,477 ($607,000 – $577,523 = $29,477) 5 százalékos relatív hiba, ami eddig a legjobb!
mikor kell használni az egyszerű vs. Többszörös lineáris regresszió
egy ingatlan értékelésekor vagy egy adott tulajdonság értékének meghatározásakor az értékelők regresszióanalízis segítségével levezethetik a legpontosabb árkorrekciókat, figyelembe véve a több tulajdonságnak az ingatlan értékére gyakorolt hatását. Az értékelési döntések adatközpontú indokolását igénylő új iparági előírások a közeljövőben még inkább szükségessé tehetik a regresszióanalízist az értékelők számára.
ne feledje, hogy nem mindig lehet többszörös lineáris regresszióanalízist használni. Ha például egy tulajdonsághoz és összehasonlíthatóságához nem áll rendelkezésre változatos adatpont-tömb, előfordulhat, hogy nem áll rendelkezésre elegendő információ az MLR-elemzés elvégzéséhez. De ha elegendő adat áll rendelkezésre az MLR-elemzés elvégzéséhez, gyakran a legpontosabb eredményeket adja. Ne feledje, hogy vannak olyan esetek, amikor egy MLR-elemzéshez további kifejezésre lesz szükség, amely a prediktorok kölcsönhatását képviseli a legpontosabban, például a fenti példában. Míg a regressziós elemzés egyértelműen nem helyettesíti az értékbecslő szakértelmét — értékes kiegészítője lehet annak.
reméljük, hogy ezeket a felismeréseket hasznosnak találja az értékeléshez.
>CE Online – 7 óra (40 államban jóváhagyva)
hogyan lehet támogatni és bizonyítani a kiigazításokat
bemutatta: Richard Hagar, SRA
Must-know üzleti gyakorlatok minden ma dolgozó értékbecslő számára. Biztosítsa a Beállítások megfelelő támogatását. A védhető kiigazítások elvégzése az első lépés az “első szintű” értékelővé váláshoz, aki többet keres, élvezi a legjobb feladatokat, és kevesebb gubancot és visszahívást szenved. Fel a játékot, ne időigényes visszahívások és keresni jóváhagyott CE ma! Iratkozzon Fel Most! $119 (7 óra)
OREP biztosított ára: $ 99
A szerzőről
Dr. Keying Ye a San Antonio-i Texasi Egyetem Üzleti Kollégiumának statisztikai professzora, valamint a HouseCanary vezető kutatója, ahol prediktív elemzéseket fejleszt a vezető értékelési szoftver, a HouseCanary Appraiser és egyéb termékek számára. HouseCanary értékbecslő segít lakossági értékbecslők közel több Üzleti keresztül egy könnyen használható megoldás, és magában foglalja a formák, mint a 1004, 2055, 1075, és így tovább!
