a felmérés minden építési munka elengedhetetlen előzetes lépése.
a teljes helyszínterv meghatározza az épület vagy a helyszín szerkezetét. Számos felmérési módszerünk van a telek természetének megértéséhez.
- Láncfelmérés
- Síkasztalfelmérés
- Iránytűfelmérés
- topográfiai felmérés stb
mindössze annyit tesz, hogy a tényleges méréseket papírra rögzíti a terület egyszerű kiszámítása érdekében. De hogyan kell kiszámítani a telek területét?
hogyan kell kiszámítani a telek területét?
a terület nem más, mint bármely geometriai alak által elfoglalt tér. Az alapvető területszámításokhoz az alábbi képleteket használhatjuk.
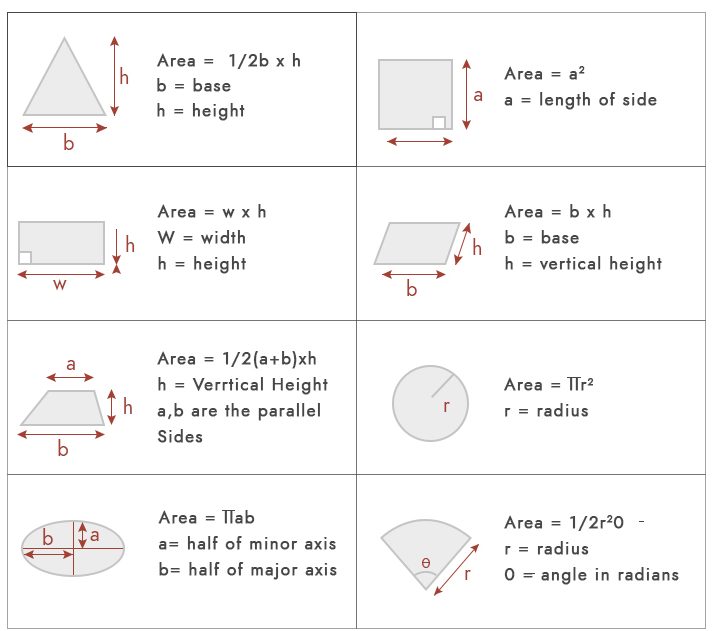
de gyakorlati szempontból a telek nagy része nem tartozik e geometriai alakzatok alá. A telekterületek leggyakoribb típusai:
- háromszög alakú telek
- szabálytalan sokszögek
- négyzet vagy téglalap
a képletek szemléltetésére, feltételezve, hogy a telkek különböző formájúak.
háromszög telek
feltételezve, hogy van egy háromszög 40 láb bázis & szélessége.
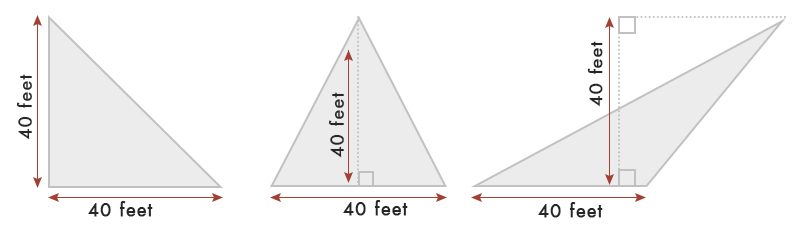
a táblázat szerint a háromszög területe = 6 x alap x szélesség = 40 x 40 = 80 négyzetkilométer.ft
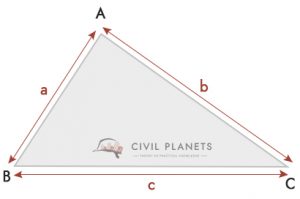
ha nem tudja megmérni a háromszög magasságát, és nem derékszögű, akkor használhatja az alábbi képletet
![]()
ahol S = háromszög kerülete = (a + b + c)/2
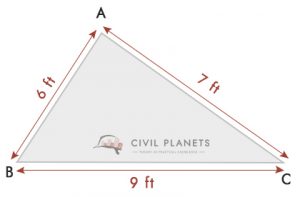
a rajzból, a = 6 láb, b = 9 láb & c = 7 láb, S = (6+9+7)/2 = 11
ezért a telek területe = S(S-A)(S-b) (S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.Ft 61 négyzetkilométer.ft
szabálytalan sokszögek
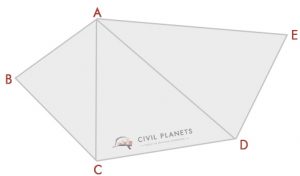
legtöbben felismertük ezt a fajta cselekményt. Ennek az alaknak a területének megtalálásához trigonometriai számítást kell használnunk. Nem olyan nehéz.
találjuk meg ennek az alaknak a területét két tipikus esetben
- szabálytalan sokszögek (ismert metszéspontméretekkel)
- szabálytalan sokszögek (szögekkel)
szabálytalan sokszögek (ismert metszéspontméretekkel)
képzelje el, hogy a következő ábra van, ismert metszéspontméretekkel.
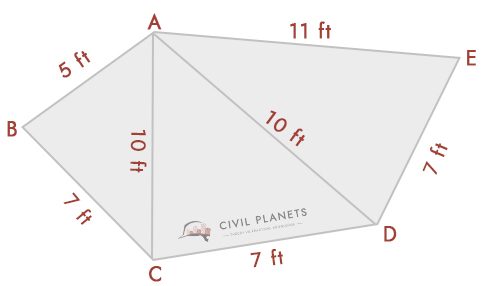
a fenti háromszög alakú képlet segítségével ezt megoldhatjuk. A diagramból három háromszög van, nevezetesen ABC, ACD, & ADE
- 1 – es háromszög-ABC, ahol S = (5+7+10)/2 = 11
a terület képlete = S(S-a)(S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- 2-es háromszög ACD, ahol S = (10+7+10)/2 = 13.5
a terület képlete = S(S-a)(S-b) (S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Ade 3. háromszög, ahol S = (10+7+11)/2 = 14
a terület képlete = S(S-a)(S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
tehát az alak teljes területe = 16.25+32.79+34.29 = 83,33 négyzetkilométer.ft
szabálytalan sokszögek (szögekkel)
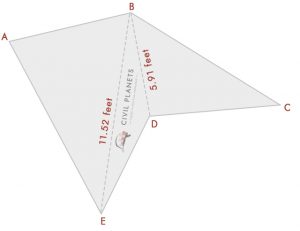
feltételezve, hogy most nem tudjuk, hogy a metszéspont mérése csak olyan szögekkel rendelkezik, mint a pic
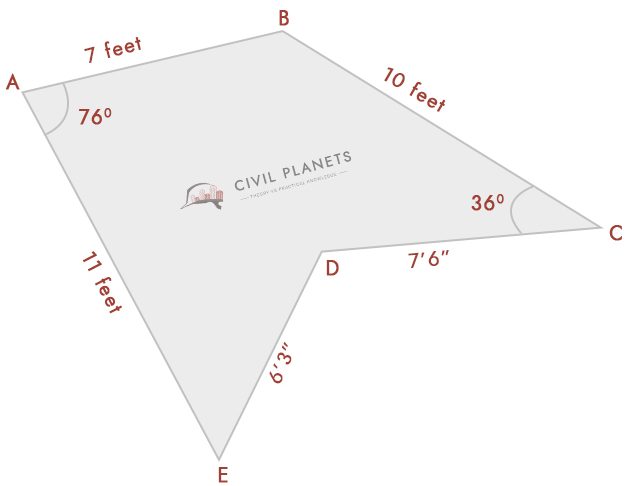
Most válassza szét a fenti képet három háromszögre az alábbiak szerint
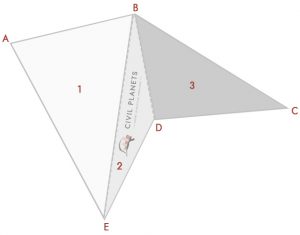
most 3 háromszögünk van, mint a fenti, csak a kereszteződés dimenziója helyett; szögeink vannak. Tehát az első dolog az, hogy ki kell számolnunk a metszéspont mérését trigonometria segítségével.
a metszéspont mérését a Heron képletével lehet elérni c2 = a2 + b2-2abcos (C)
ahol a = AB hossza, b = ae hossza, c = EB hossza
Eb hossza = ons(a2 + b2 – 2abcos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 láb
DB = Hossz(a2 + b2 – 2abcos(C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 láb
most már tudjuk, hogy a hossza minden oldalon, a háromszög képlet segítségével tudjuk kiszámítani a terület most
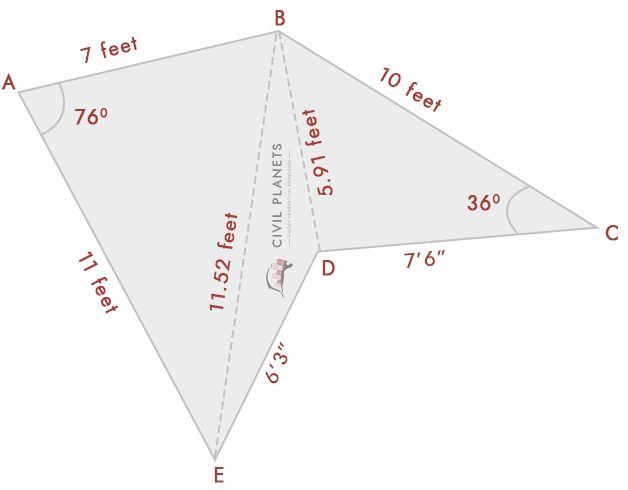
a diagramból három háromszög van
háromszög 1-Abe, ahol S = (7+11+11.52)/2 = 14.76
a terület képlete = S(S-a)(S-b) (S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
2 – es háromszög-főág, ahol S = (11.52+6.25+5.91)/2 = 11.84
a terület képlete = S(S-a)(S-b) (S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
BDC 3. háromszög, ahol S = (5.91+7.5+10)/2 = 11.70
a terület képlete = S(S-a)(S-b) (S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
tehát az alak teljes területe = 37.35+11.21+21.99 = 70,55 négyzetméter.ft
Boldog tanulás 🙂
