Maanmittaus on välttämätön ennakkovaihe kaikissa rakennustöissä.
koko asemakaava määrittää rakennuksen tai alueen rakenteen. Meillä on lukuisia maanmittausmenetelmiä tontin luonteen ymmärtämiseksi.
- Ketjumittaus
- Tasomittaus
- Kompassimittaus
- Topografinen Maanmittaus jne
siinä ei tehdä muuta kuin kirjataan todelliset mittaukset paperille, jotta pinta-ala voidaan laskea helposti. Mutta miten laskea Tontin pinta-ala?
Miten lasketaan Havaintoala?
alue ei ole muuta kuin minkä tahansa geometrisen muodon täyttämä tila. Perusaluelaskennoissa voisimme käyttää alla olevia kaavoja.
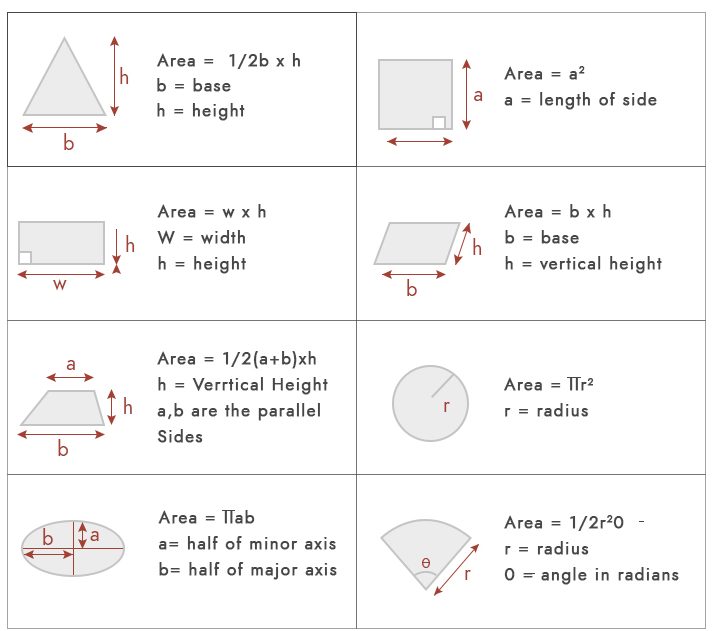
mutta käytännössä suurin osa tontista ei kuulu näihin geometrisiin muotoihin. Yleisimpiä piirrosalatyyppejä ovat
- kolmikulmainen kuvaaja
- epäsäännöllinen monikulmio
- neliö tai suorakulmainen
kaavojen kuvaamiseksi olettaen, että kuvaajilla on eri muotoisia kuvioita.
kolmion tontti
olettaen, että meillä on kolmio, jonka 40 jalan pohja & leveys.
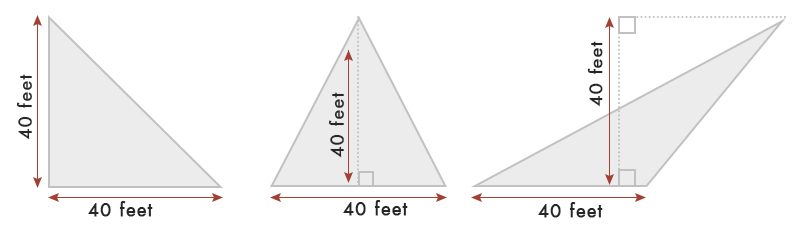
taulukon mukaisesti kolmion pinta-ala = ½ x perus x Leveys = ½ x 40 x 40 = 80 neliömetriä.ft
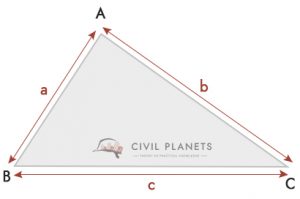
jos kolmion korkeutta ei pysty mittaamaan ja jos se ei ole suorassa kulmassa, voidaan käyttää alla olevaa kaavaa
Hebrons Formula_447 >
missä S = kolmion ympärysmitta = (a + b + c)/2
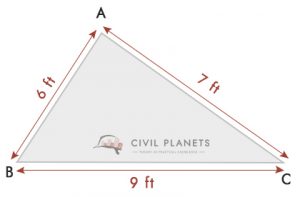
piirustuksesta, a = 6 jalkaa, b = 9 jalkaa & c = 7 jalkaa, S = (6+9+7)/2 = 11
näin ollen havaintoalan pinta-ala = √S (S-a) (S-b) (S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft ≅ 21 Sq.ft
epäsäännöllinen monikulmio
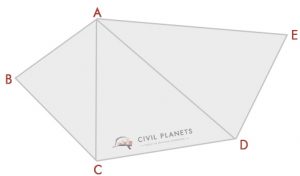
useimmat tunnistaisivat tällaisen juonen. Tämän muodon alueen löytämiseksi on käytettävä trigonometrian laskentaa. Ei se ole niin vaikeaa.
etsitään tämän muodon alue kahdessa tyypillisessä tapauksessa
- epäsäännölliset Monikulmiot (joiden leikkauspistemitat tunnetaan)
- epäsäännölliset Monikulmiot (joiden kulmat)
epäsäännölliset Monikulmiot (joiden leikkauspistemitat tunnetaan)
Kuvittele, että meillä on seuraava kuvaaja, jonka leikkauspistemitat tunnetaan.
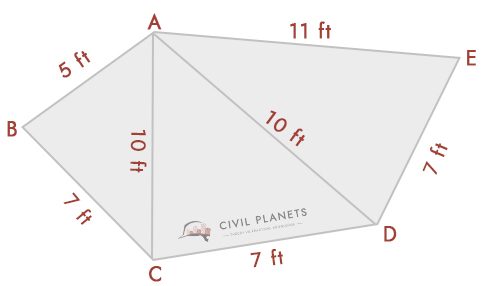
käyttämällä edellä kolmiomainen kaava, voimme ratkaista tämän. Kaaviosta saadaan kolme kolmiota eli ABC, ACD, & ADE
- kolmio 1-Δ ABC, jossa S = (5+7+10)/2 = 11
Pinta-alan kaava = √S (S-a) (S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- kolmio 2-Δ ACD, jossa S = (10+7+10)/2 = 13.5
Pinta-alan kaava = √S (S-a) (S-b) (S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- kolmio 3-Δ ADE, jossa S = (10+7+11)/2 = 14
Pinta-alan kaava = √S (S-a) (S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
joten muodon kokonaispinta-ala = 16.25+32.79+34.29 = 83,33 neliömetriä.ft
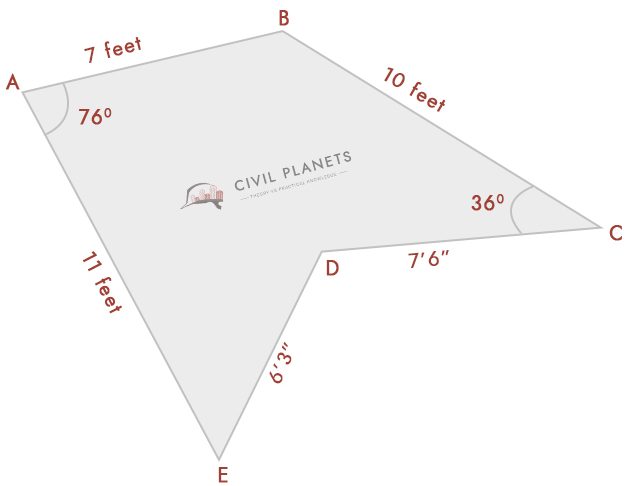
epäsäännölliset Monikulmiot (kulmilla)
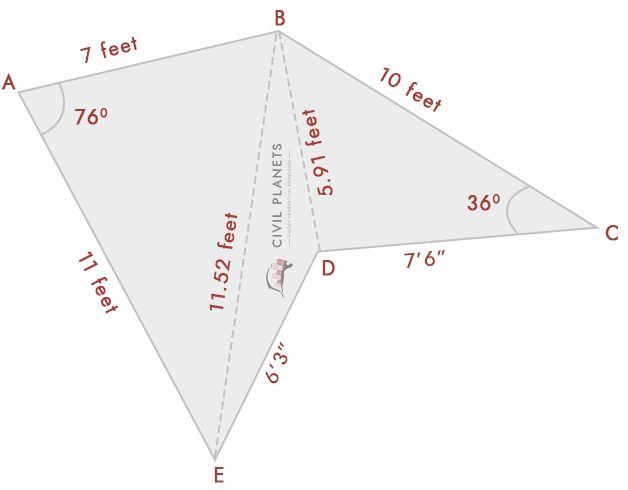
olettaen, että nyt emme tiedä leikkauspistemittausta, jossa on vain kulmat kuten kuvan alapuolella
erottele nyt yllä oleva kuva kolmeksi kolmioksi, kuten alla
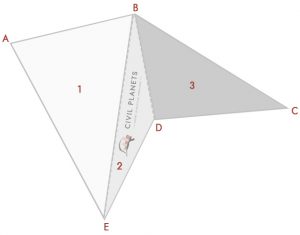
nyt meillä on 3 kolmiot aivan kuten edellä, vain asia sen sijaan, risteysalueiden ulottuvuus; meillä on kulmat. Joten ensimmäinen asia on meidän täytyy laskea risteysalueiden mittaus käyttäen trigonometriaa.
leikkauspistemittaus saadaan Heronin kaavalla formula_2 = a2 + b2 – 2abcos(C)
jossa A = AB: n pituus, b = AE: n pituus, c = EB: n pituus
EB: n pituus = √(a2 + b2 – 2abCos (C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 jalat
dB: n pituus = √(a2 + b2-2abcos (C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 jalkaa
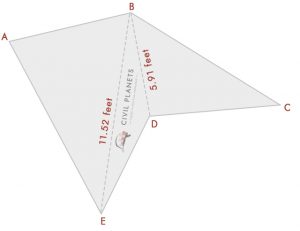
nyt tiedämme jokaisen sivun pituuden käyttämällä kolmion kaavaa, voimme laskea alueen nyt
kaaviosta saadaan kolme kolmiota
kolmio 1-Δ ABE, jossa S = (7+11+11.52)/2 = 14.76
Pinta-alan kaava = √S (S-a) (S-b) (S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
kolmio 2-Δ BED, jossa S = (11.52+6.25+5.91)/2 = 11.84
Pinta-alan kaava = √S (S-a) (S-b) (S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
kolmio 3-Δ BDC, jossa S = (5.91+7.5+10)/2 = 11.70
Pinta-alan kaava = √S (S-a) (S-b) (S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
joten muodon kokonaispinta-ala = 37.35+11.21+21.99 = 70,55 neliömetriä.ft
Happy Learning 🙂
