La topografía es un paso preliminar esencial para cualquier trabajo de construcción.
El plan de sitio completo determina la estructura de un edificio o un sitio. Tenemos numerosos métodos de agrimensura para comprender la naturaleza de una parcela.
- Topografía en cadena
- Topografía de Mesa plana
- Topografía con brújula
- Topografía, etc
Todo lo que hace es registrar las mediciones reales en un papel para calcular fácilmente el área. Pero, ¿cómo calcular el área de la parcela?
¿Cómo calcular el Área de la Parcela?
El área no es más que un espacio ocupado por cualquier forma geométrica. Para cálculos de área básicos, podríamos usar las siguientes fórmulas.
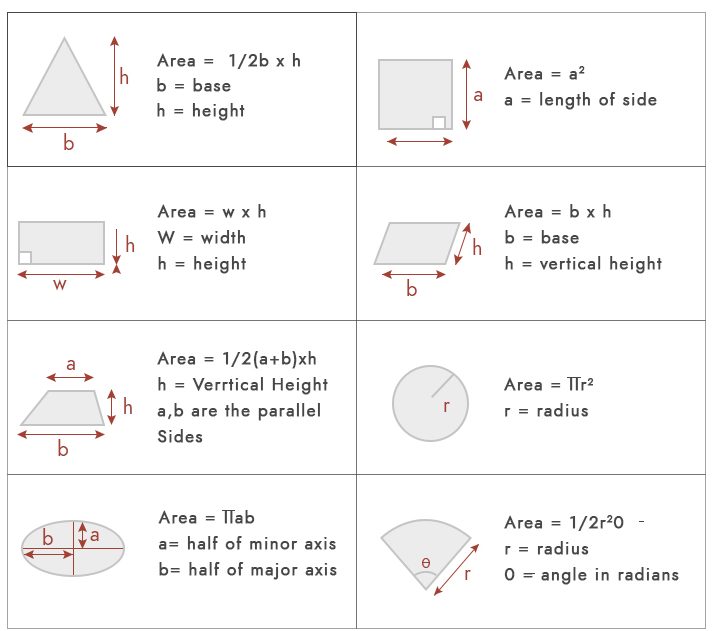
Pero en términos prácticos, la mayor parte de la trama no cae bajo estas formas geométricas. Los tipos más comunes de áreas de parcela son
- Parcela Triangular
- Polígonos irregulares
- Cuadrados o rectangulares
Para ilustrar las fórmulas, asumiendo que tenemos diferentes formas de parcelas.
Diagrama de triángulo
Asumiendo que tenemos un triángulo de 40 pies de base & de ancho.
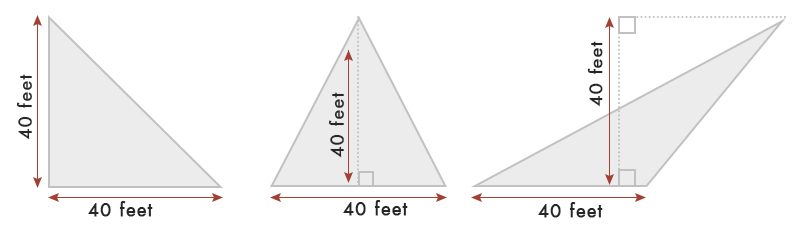
Según la tabla, el Área del triángulo = ½ x base x ancho = ½ x 40 x 40 = 80 Sq.ft
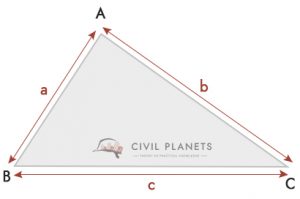
Si usted no puede ser capaz de medir la altura del triángulo y si no es un ángulo recto, entonces usted podría utilizar la siguiente fórmula
![]()
Donde S = Perímetro del triángulo = (a + b + c)/2
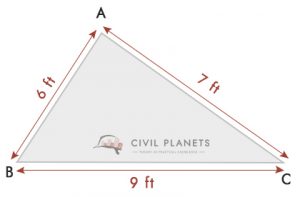
en el dibujo, a = 6 pies, b = 9 pies & c = 7 pies, S = (6+9+7)/2 = 11
por lo Tanto, Área de la parcela = √S(S-a)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.21 pies cuadrados.ft
Polígonos irregulares
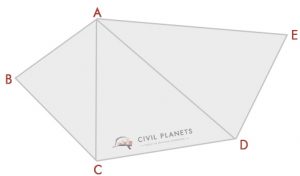
La mayoría de nosotros podría reconocer este tipo de trama. Para encontrar el área de esta forma, tenemos que usar el cálculo de trigonometría. No es tan difícil.
Encontremos el área de esta forma en dos casos típicos
- Polígonos irregulares (con dimensiones de intersección conocidas)
- Polígonos irregulares (con ángulos)
Polígonos irregulares (con dimensiones de intersección conocidas)
Imagine que tenemos la siguiente gráfica, con dimensiones de intersección conocidas.
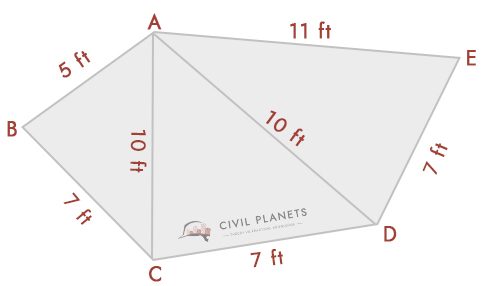
Usando la fórmula triangular anterior, podemos resolver esto. Del diagrama, tenemos tres triángulos, a saber, ABC, ACD, & ADE
- Triángulo 1 – Δ ABC, Donde S = (5+7+10)/2 = 11
Fórmula para el área = √S(S-a)(S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Triángulo 2 – Δ ACD, Donde S = (10+7+10)/2 = 13.5
Fórmula para el Área = √S(S-a)(S-b)(S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Triángulo 3-Δ ADE, Donde S = (10+7+11)/2 = 14
Fórmula para el área = √S(S-a)(S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
So área total de la forma = 16.25+32.79+34.29 = 83,33 Metros cuadrados.ft
Polígonos irregulares (con ángulos)
Suponiendo que ahora no conocemos la medición de intersección que solo tiene ángulos como la imagen inferior
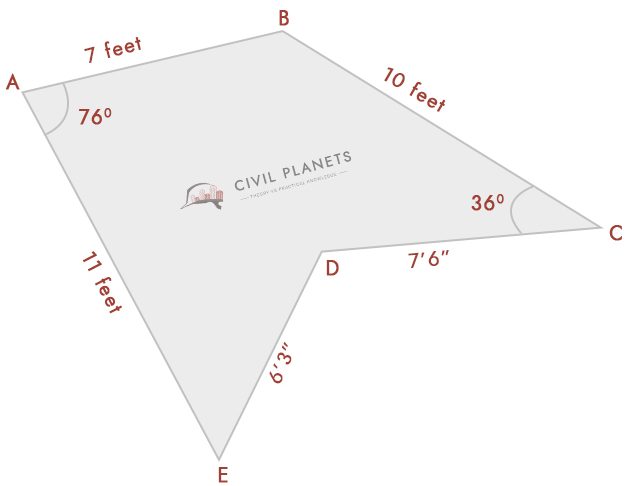
Ahora separe la imagen de arriba en tres triángulos como abajo
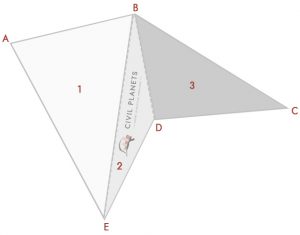
Ahora tenemos 3 triángulos como el anterior, lo único en lugar de la dimensión de intersección; tenemos ángulos. Así que lo primero es que tenemos que calcular la medición de intersección usando trigonometría.
La medición de intersección se puede obtener mediante la fórmula de Heron c2 = a2 + b2-2abCos (C)
Donde, a = longitud de AB, b = longitud de AE, c = longitud de EB
Longitud de EB = √(a2 + b2-2abCos(C))
= √(72 + 112 – 2 * 7 * 11 * Ocs(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 pies
Longitud de DB = √(a2 + b2-2abCos (C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Oc(36°)) = √(156.25 – 121.35) = 5.91 pies
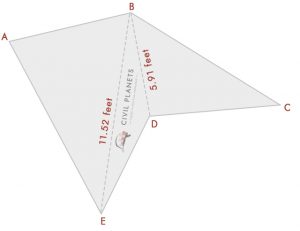
Ahora sabemos la longitud de cada lado, usando la fórmula de triángulo, podemos calcular el área ahora
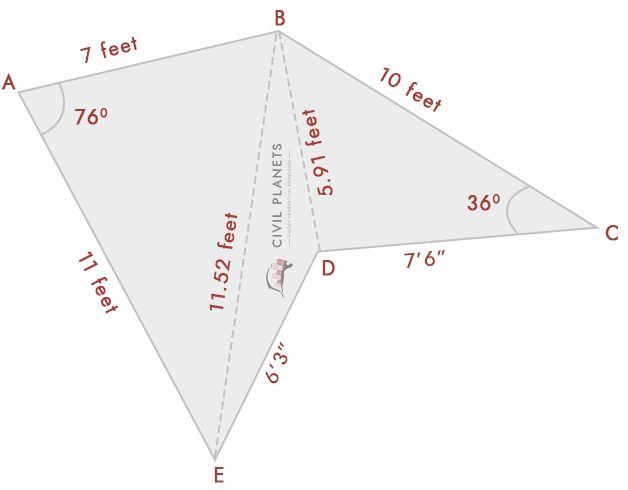
Del diagrama, tenemos tres triángulos
Triángulo 1-Δ ABE, Donde S = (7+11+11.52)/2 = 14.76
Fórmula para el área = √S(S-a)(S-b) (S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
Triángulo 2 – Δ CAMA, Donde S = (11.52+6.25+5.91)/2 = 11.84
Fórmula para el Área = √S(S-a)(S-b)(S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
Triángulo 3 – Δ BDC, Donde S = (5.91+7.5+10)/2 = 11.70
Fórmula para el Área = √S(S-a)(S-b)(S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
So área total de la forma = 37.35+11.21+21.99 = 70,55 Metros cuadrados.ft
Aprendizaje feliz 🙂
