landmåling er et vigtigt indledende trin for ethvert byggearbejde.
hele grundplanen bestemmer strukturen for en bygning eller et sted. Vi har adskillige metoder til opmåling for at forstå karakteren af et plot.
- Chain Surveying
- Plane Table Surveying
- Compass Surveying
- topografisk Surveying etc
alt det gør er at registrere de faktiske målinger i et papir for nem beregning af areal. Men hvordan man beregner plotområdet?
hvordan beregnes Plotareal?
området er intet andet end et rum besat af enhver geometrisk form. Til grundlæggende områdeberegninger kunne vi bruge nedenstående formler.
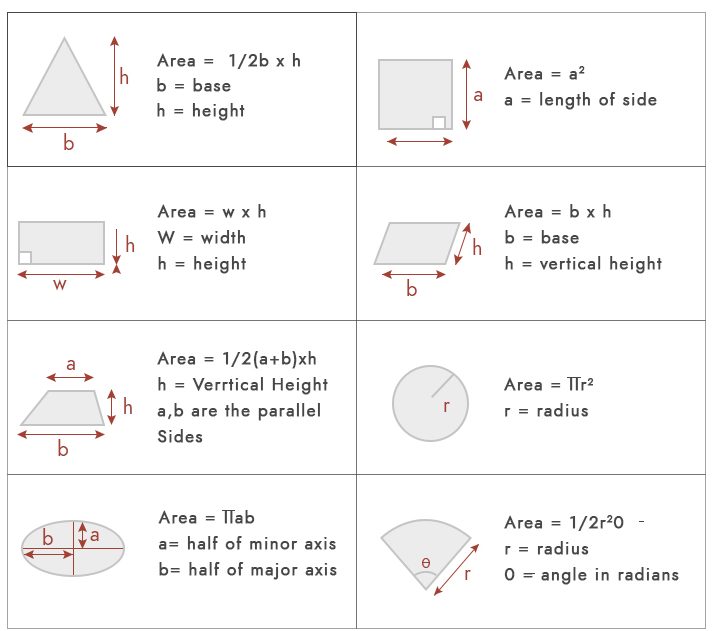
men i praksis falder det meste af plottet ikke under disse geometriske former. Mest almindelige typer af plotområder er
- trekantet Plot
- uregelmæssige polygoner
- firkantet eller rektangulært
for at illustrere formlerne, forudsat at vi har forskellige former for plot.
Triangle plot
forudsat at vi har en trekant på 40 fod base & bredde.
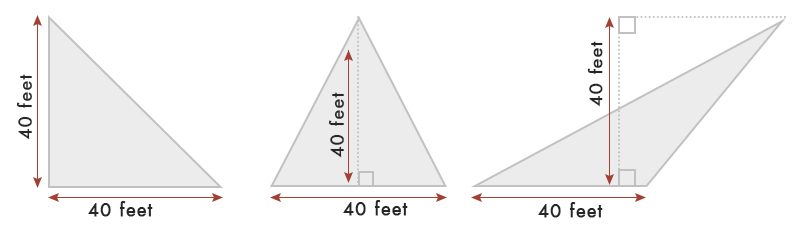
i henhold til tabellen er arealet af trekanten = 40 gange 40 = 80 kvm.ft
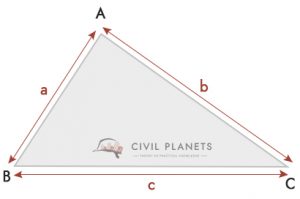
hvis du ikke kan måle højden på trekanten, og hvis den ikke er en ret vinkel, kan du bruge nedenstående formel
![]()
hvor S = omkreds af Trekant = (a + b + c)/2
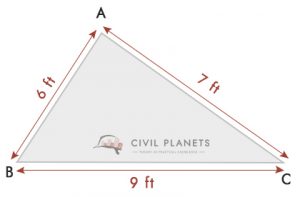
fra tegningen, a = 6 fod, b = 9 fod & c = 7 fod, S = (6+9+7)/2 = 11
derfor er arealet af plottet = Kurt S(S-A)(S-b)(S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 kvm.ft 21 kvm.ft
uregelmæssige polygoner
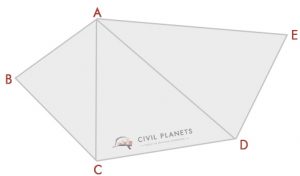
de fleste af os kunne genkende denne slags plot. For at finde området med denne form skal vi bruge trigonometriberegning. Det er ikke så svært.
lad os finde området med denne form i to typiske tilfælde
- uregelmæssige polygoner (med kendte krydsdimensioner)
- uregelmæssige polygoner (med vinkler))
uregelmæssige polygoner(med kendte krydsdimensioner)
Forestil dig, at vi har følgende plot med kendte krydsdimensioner.
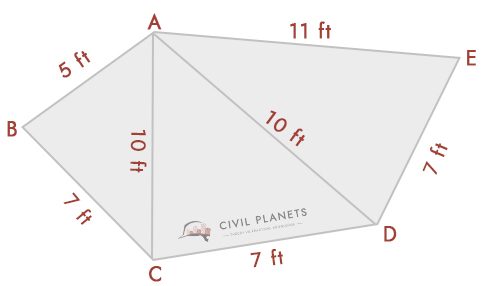
ved hjælp af ovenstående trekantede formel kan vi løse dette. Fra diagrammet har vi tre trekanter, nemlig ABC, ACD, & ADE
- Triangle 1-list ABC, hvor S = (5+7+10)/2 = 11
formel for Område = kur S(S-A)(S-b)(S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 kvm.ft
- Triangle 2-ret ACD, hvor S = (10+7+10)/2 = 13.5
formel for Område = kur S(S-A)(S-b)(S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 kvm.ft
- Triangle 3-ret ADE, hvor S = (10+7+11)/2 = 14
formel for Område = kur S(S-A)(S-b)(S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 kvm.ft
så samlet areal af formen = 16.25+32.79+34.29 = 83,33 kvm.ft
uregelmæssige polygoner (med vinkler)
forudsat at vi nu ikke kender skæringsmålingen kun med vinkler som nedenfor pic
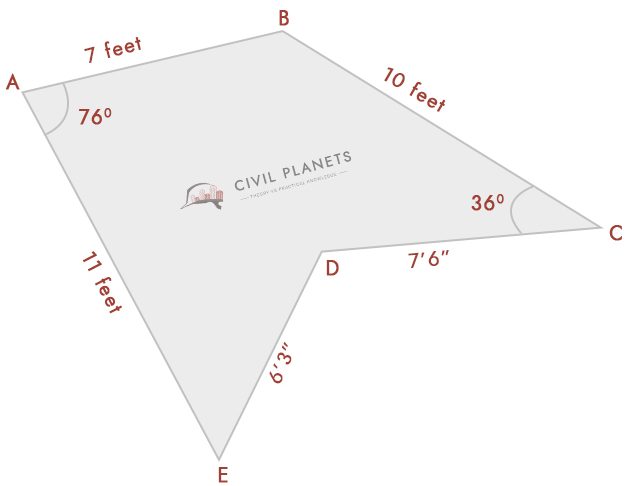
nu adskille ovenstående billede i tre trekanter som nedenfor
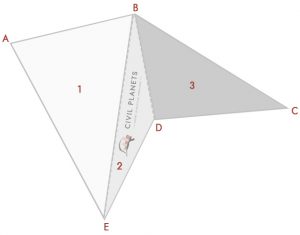
nu har vi 3 trekanter ligesom ovenstående, kun ting i stedet for skæringsdimensionen; vi har vinkler. Så den første ting er, at vi skal beregne skæringsmåling ved hjælp af trigonometri.
skæringsmålingen kan opnås ved hjælp af Herons formel c2 = a2 + b2 – 2abcos (C)
hvor, A = længde af AB, b = længde af AE, c = længde af EB
længde af EB = kur(a2 + b2-2abcos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 fødder
længde af DB = liter(a2 + b2-2abcos (C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 fødder
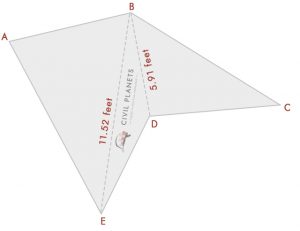
nu ved vi længden af hver side, ved hjælp af trekanten formel, kan vi beregne området nu
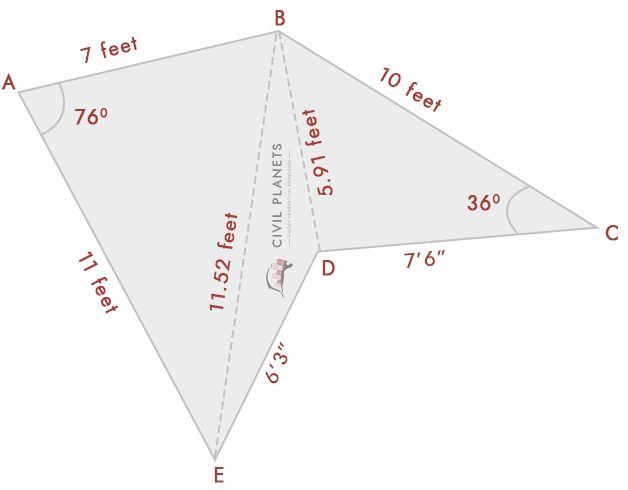
fra diagrammet har vi tre trekanter
Trekant 1-bogstav ABE, hvor S = (7+11+11.52)/2 = 14.76
formel for Område = kur S(S-A)(S-b)(S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 kvm.ft
Triangle 2-liter seng, hvor S = (11.52+6.25+5.91)/2 = 11.84
formel for Område = kur S(S-A)(S-b)(S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 kvm.ft
Triangle 3-ret BDC, hvor S = (5.91+7.5+10)/2 = 11.70
formel for Område = kur S(S-A)(S-b)(S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 kvm.ft
så samlet areal af formen = 37.35+11.21+21.99 = 70,55 kvm.ft
glad læring 🙂
