průzkum je nezbytným předběžným krokem pro jakékoli stavební práce.
celý plán lokality určuje strukturu budovy nebo místa. Máme řadu metod průzkumu, abychom pochopili povahu spiknutí.
- Chain geodetické
- rovina tabulka geodetické
- Compass geodetické
- topografické geodetické etc
vše, co dělá, je záznam skutečné měření do papíru pro snadný výpočet plochy. Ale jak vypočítat plochu pozemku?
Jak vypočítat plochu pozemku?
oblast není nic jiného než prostor obsazený jakýmkoli geometrickým tvarem. Pro základní výpočty oblasti bychom mohli použít níže uvedené vzorce.
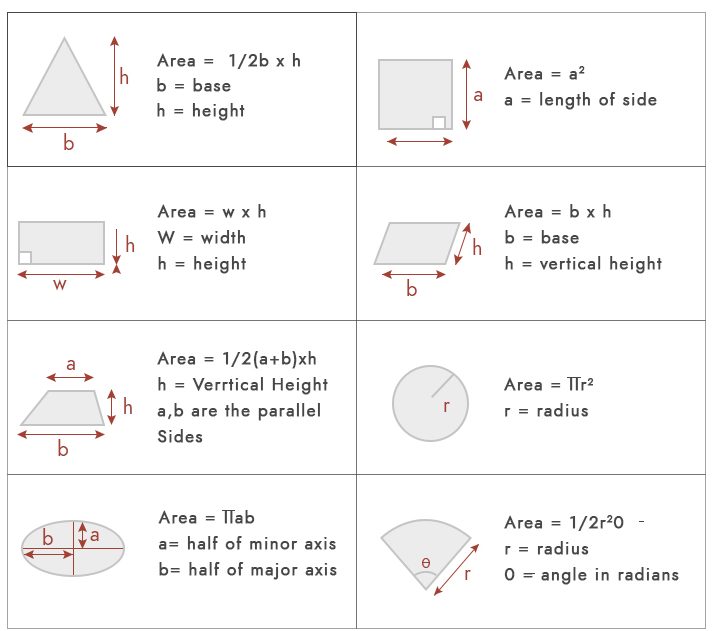
z praktického hlediska však většina pozemku nespadá pod tyto geometrické tvary. Nejběžnější typy ploch pozemku jsou
- trojúhelníkový pozemek
- nepravidelné mnohoúhelníky
- čtvercové nebo obdélníkové
pro ilustraci vzorců, za předpokladu, že máme různé tvary pozemků.
trojúhelník plot
za předpokladu, že máme trojúhelník 40 stop základny & šířka.
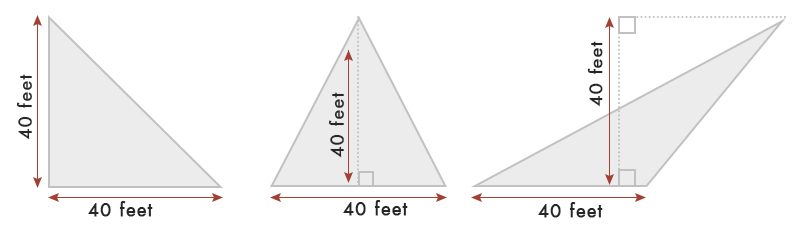
podle tabulky, plocha trojúhelníku = ½ x základna x šířka = ½ x 40 x 40 = 80 čtverečních.ft
pokud nemůžete měřit výšku trojúhelníku a pokud to není pravý úhel, můžete použít níže uvedený vzorec
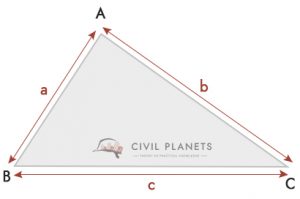
![]()
kde s = obvod trojúhelníku = (a + b + c)/2
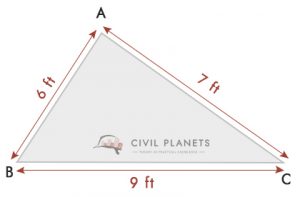
z výkresu a = 6 stop, b = 9 stop & c = 7 stop, S = (6+9+7)/2 = 11
proto plocha pozemku = √s(S-a)(S-b) (S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.ft ≅ 21 čtverečních.ft
nepravidelné mnohoúhelníky
většina z nás by mohla rozpoznat tento druh spiknutí. Chcete-li najít oblast tohoto tvaru, musíme použít výpočet trigonometrie. Není to tak těžké.
najdeme plochu tohoto tvaru ve dvou typických případech
- nepravidelné mnohoúhelníky (se známými rozměry průsečíku)
- nepravidelné mnohoúhelníky (s úhly)
nepravidelné mnohoúhelníky (se známými rozměry průsečíku)
Představte si, že máme následující graf se známými rozměry průsečíku.
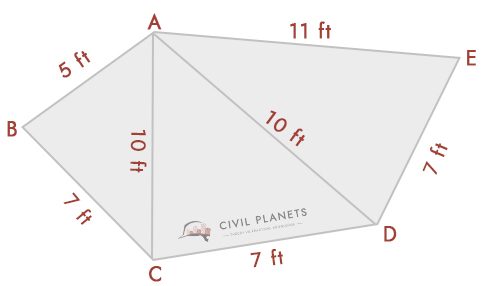
pomocí výše uvedeného trojúhelníkového vzorce to můžeme vyřešit. Z diagramu máme tři trojúhelníky a to ABC, ACD, & ADE
- trojúhelník 1-Δ ABC, kde S = (5+7+10)/2 = 11
vzorec pro oblast = √S(S-a) (S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- trojúhelník 2-Δ ACD, kde S = (10+7+10)/2 = 13.5
vzorec pro oblast = √S(S-a) (S-b) (S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- trojúhelník 3-Δ ADE, kde S = (10+7+11)/2 = 14
vzorec pro oblast = √S(S-a) (S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
takže celková plocha tvaru = 16.25+32.79+34.29 = 83,33 Sq.ft
nepravidelné mnohoúhelníky (s úhly)
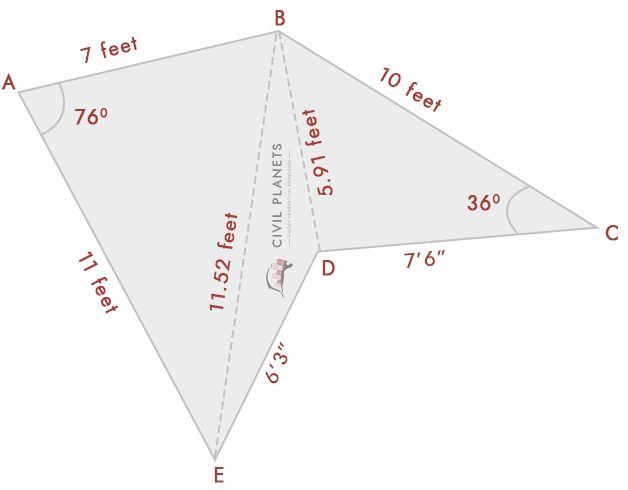
za předpokladu, že nyní nevíme, že měření průsečíku má pouze úhly jako pod obr.
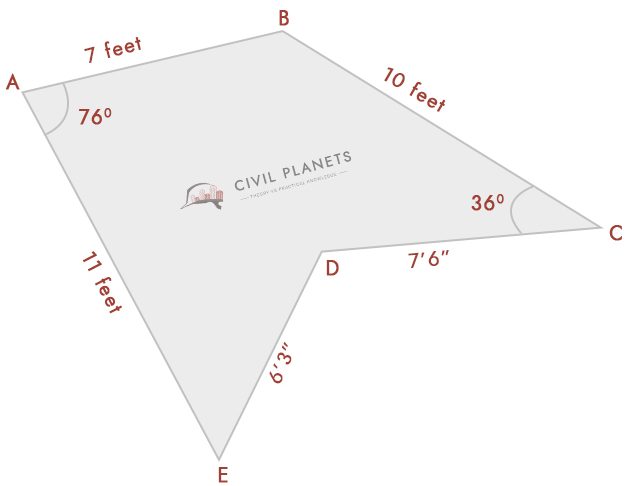
nyní oddělte výše uvedený obrázek do tří trojúhelníků, jak je uvedeno níže
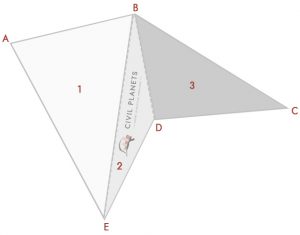
nyní máme 3 trojúhelníky stejně jako výše, jediná věc místo průsečíku dimenze; máme úhly. Takže první věc je, že musíme vypočítat měření průsečíku pomocí trigonometrie.
měření průsečíku lze získat Heronovým vzorcem c2 = a2 + b2-2abCos (C)
kde a = délka AB, b = Délka AE, c = délka EB
Délka EB = √(a2 + b2-2abCos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 nohy
Délka DB = √(a2 + b2-2abCos (C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 Stop
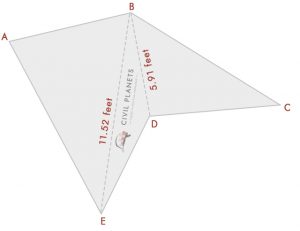
nyní známe délku každé strany, pomocí trojúhelníkového vzorce můžeme vypočítat plochu nyní
z diagramu máme tři trojúhelníky
trojúhelník 1-Δ ABE, kde S = (7+11+11.52)/2 = 14.76
vzorec pro oblast = √S(S-a) (S-b) (S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
trojúhelník 2-Δ lože, kde S = (11.52+6.25+5.91)/2 = 11.84
vzorec pro oblast = √S(S-a) (S-b) (S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.ft
trojúhelník 3-Δ BDC, kde S = (5.91+7.5+10)/2 = 11.70
vzorec pro oblast = √S(S-a) (S-b) (S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
takže celková plocha tvaru = 37.35+11.21+21.99 = 70.55 Sq.ft
šťastné učení 🙂
