L’arpentage est une étape préliminaire essentielle pour tout travail de construction.
Le plan d’ensemble du site détermine la structure d’un bâtiment ou d’un site. Nous avons de nombreuses méthodes d’arpentage pour comprendre la nature d’une parcelle.
- Arpentage en chaîne
- Arpentage sur Table plane
- Arpentage au compas
- Arpentage topographique etc
Tout ce qu’il fait est d’enregistrer les mesures réelles dans un papier pour un calcul facile de la surface. Mais comment calculer la superficie de la parcelle?
Comment calculer la surface de la parcelle?
La zone n’est rien d’autre qu’un espace occupé par une forme géométrique quelconque. Pour les calculs de surface de base, nous pourrions utiliser les formules ci-dessous.
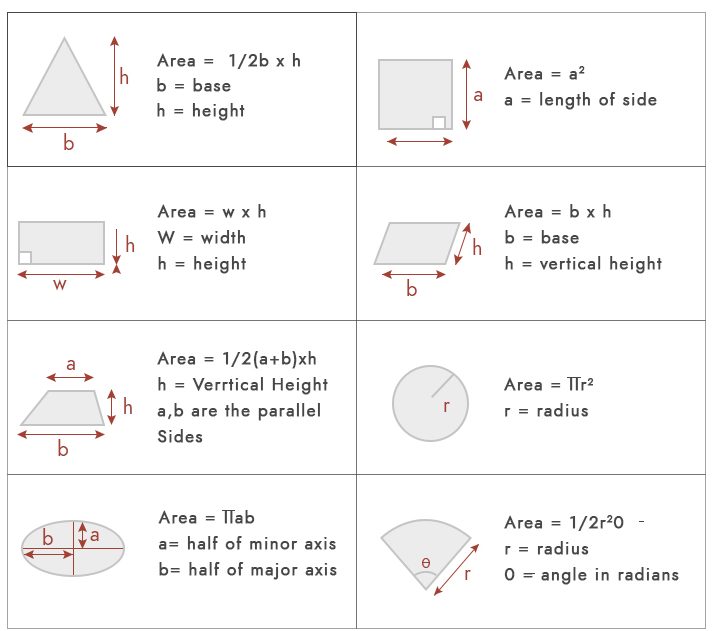
Mais en termes pratiques, la plupart de l’intrigue ne relèvent pas de ces formes géométriques. Les types les plus courants de zones de parcelle sont
- Parcelle triangulaire
- Polygones irréguliers
- Carrés ou rectangulaires
Pour illustrer les formules, en supposant que nous avons différentes formes de parcelles.
Tracé du triangle
En supposant que nous ayons un triangle de 40 pieds de base & de largeur.
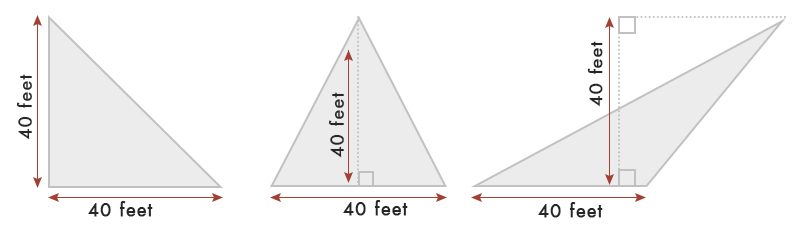
Selon le tableau, Surface du triangle = ½ x base x largeur = ½ x 40 x 40 = 80 mètres carrés.pi
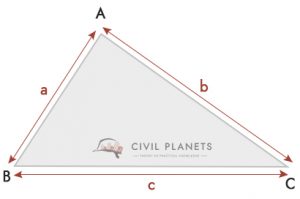
Si vous ne pouvez pas mesurer la hauteur du triangle et si ce n’est pas un angle droit, vous pouvez utiliser la formule ci-dessous
![]()
Où S = Périmètre du triangle = (a + b + c)/2
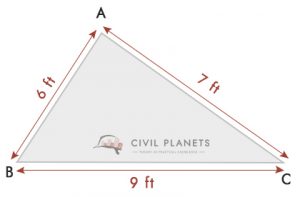
D’après le dessin, a = 6 pieds, b = 9 pieds & c = 7 pieds, S = (6+9+7)/2 = 11
Par conséquent, l’aire de la parcelle = √S (S-a) (S-b) (S-c) = √11*(11-6)*(11-9)*(11-7) = 20.97 Sq.pi 2 21 Sq.ft
Polygones irréguliers
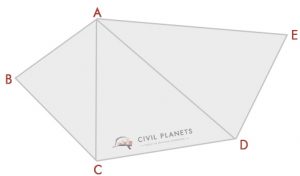
La plupart d’entre nous pourraient reconnaître ce genre de complot. Pour trouver l’aire de cette forme, nous devons utiliser le calcul de trigonométrie. Ce n’est pas si difficile.
Trouvons l’aire de cette forme dans deux cas typiques
- Polygones irréguliers (avec des dimensions d’intersection connues)
- Polygones irréguliers (avec des angles)
Polygones irréguliers (avec des dimensions d’intersection connues)
Imaginez que nous ayons le tracé suivant, avec des dimensions d’intersection connues.
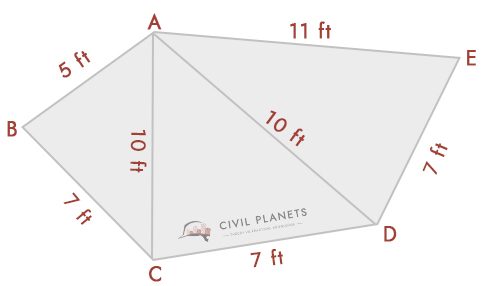
En utilisant la formule triangulaire ci-dessus, nous pouvons résoudre ce problème. À partir du diagramme, nous avons trois triangles à savoir ABC, ACD, & ADE
- Triangle 1-Δ ABC, Où S = (5+7+10)/2 = 11
Formule pour l’aire = √S (S-a) (S-b) (S-c) = √11*(11-5)*(11-7)*(11-10) = 16.25 Sq.ft
- Triangle 2– Δ ACD, Où S = (10+7+10)/2 = 13.5
Formule pour l’aire = √S (S-a) (S-b) (S-c) = √13.5*(13.5-10)*(13.5-7)*(13.5-10) = 32.79 Sq.ft
- Triangle 3–Δ ADE, Où S = (10+7+11)/2 = 14
Formule pour l’aire = √S (S-a) (S-b) (S-c) = √14*(14-10)*(14-7)*(14-11) = 34.29 Sq.ft
Donc surface totale de la forme = 16.25+32.79+34.29 = 83,33 mètres carrésft
Polygones irréguliers (avec angles)
En supposant maintenant que nous ne connaissons pas la mesure d’intersection ayant uniquement des angles comme ci-dessous pic
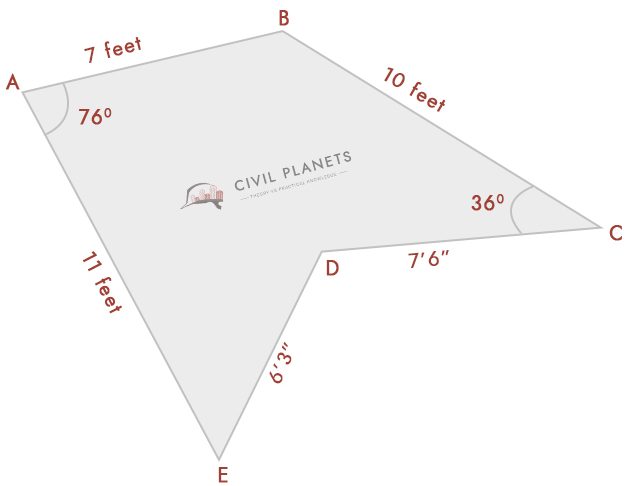
Séparez maintenant l’image ci-dessus en trois triangles comme ci-dessous
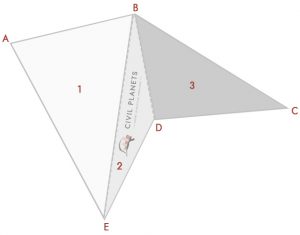
Maintenant, nous avons 3 triangles comme ci-dessus, la seule chose à la place de la dimension d’intersection; nous avons des angles. Donc, la première chose est que nous devons calculer la mesure d’intersection en utilisant la trigonométrie.
La mesure d’intersection peut être obtenue par la formule de Héron c2 = a2 + b2-2abCos(C)
Où, a = longueur de AB, b = longueur de AE, c = longueur de EB
Longueur de EB = √ (a2 + b2-2abCos(C))
= √(72 + 112 – 2 * 7 * 11 * Cos(76°)) = √(49 + 121 – 154 * 0.242) = 11.52 pieds
Longueur de DB = √ (a2 + b2-2abCos(C))
= √(102 + 7.52 – 2 *7 .5 * 10 * Cos(36°)) = √(156.25 – 121.35) = 5.91 pieds
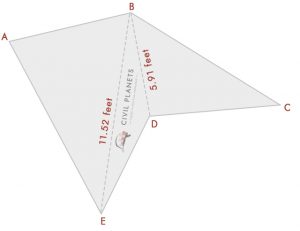
Maintenant que nous connaissons la longueur de chaque côté, en utilisant la formule du triangle, nous pouvons calculer l’aire maintenant
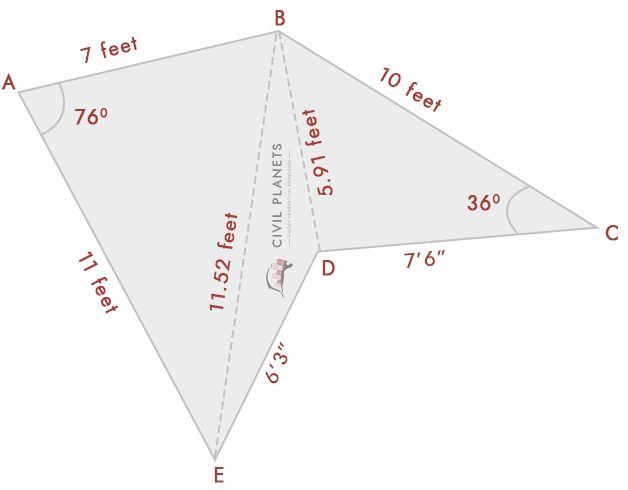
À partir du diagramme, nous avons trois triangles
Triangle 1-Δ ABE, Où S = (7+11+11.52)/2 = 14.76
Formule pour l’aire = √S (S-a) (S-b) (S-c) = √14.76*(14.76-7)*(14.76-11)*(14.76-11.52) = 37.35 Sq.ft
LIT triangulaire 2-Δ, Où S = (11.52+6.25+5.91)/2 = 11.84
Formule pour l’aire = √S (S-a) (S-b) (S-c) = √11.84*(11.84-11.52)*(11.84-6.25)*(11.84-5.91) = 11.21 Sq.triangle ft
3–Δ BDC, Où S = (5.91+7.5+10)/2 = 11.70
Formule pour l’aire = √S (S-a) (S-b) (S-c) = √11.70*(11.70-5.91)*(11.70-7.5)*(11.70-10) = 21.99 Sq.ft
Donc surface totale de la forme = 37.35+11.21+21.99 = 70,55 mètres carrésft
Bon apprentissage 🙂
