este exemplo é baseado nas estatísticas criminais do FBI de 2006. Particularmente, estamos interessados na relação entre o tamanho do estado e o número de assassinatos na cidade.
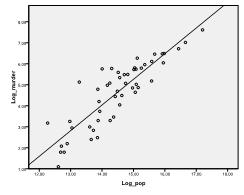
primeiro, precisamos verificar se há uma relação linear nos dados. Para isso, verificamos o gráfico de dispersão. O gráfico de dispersão indica uma boa relação linear, o que nos permite realizar uma análise de regressão linear. Também podemos verificar a correlação bivariada de Pearson e descobrir que ambas as variáveis estão altamente correlacionadas (r=.959 com p < 0,001).

Descubra Como Podemos Ajudar a Editar a Sua Dissertação Capítulos
Alinhamento de quadro teórico, coleta de artigos, sintetizando as lacunas, articulando uma metodologia clara e plano de dados, e escrever sobre os conhecimentos teóricos e implicações práticas de sua pesquisa são parte do nosso abrangente dissertação de serviços de edição.
- traga a experiência de edição de dissertação para os capítulos 1-5 em tempo hábil.
- Acompanhe todas as mudanças e, em seguida, trabalhe com você para criar uma escrita acadêmica.
- suporte contínuo para abordar o feedback do Comitê, reduzindo as revisões.
em Segundo lugar, precisamos verificar a normalidade multivariada. Em nosso exemplo, descobrimos que a normalidade multivariada pode não estar presente.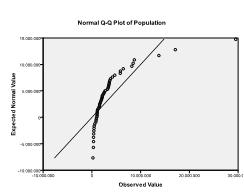
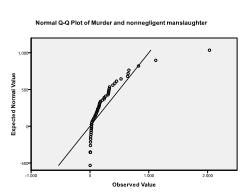
O teste de Kolmogorov-Smirnov confirma essa suspeita (p = 0,002 e p = 0.006). Conduzir uma transformação ln nas duas variáveis corrige o problema e estabelece a normalidade multivariada (teste K-S p=.991 e p = .543).
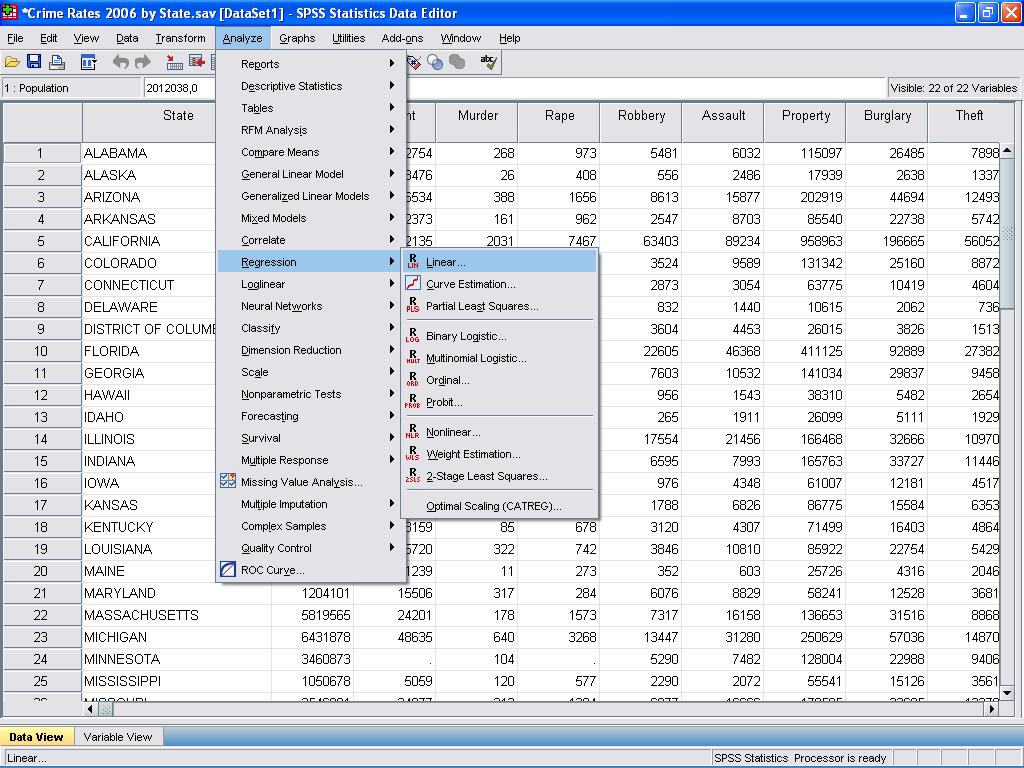
agora podemos realizar a análise de regressão linear. A regressão Linear é encontrado em SPSS na Análise/Regressão/Linear…
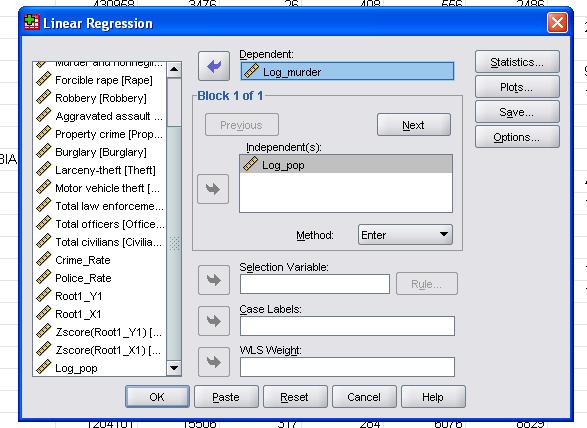
neste caso simples, precisamos apenas adicionar as variáveis de log_pop e log_murder para o modelo como dependente e as variáveis independentes.
As estatísticas de campo nos permite incluir estatísticas adicionais que precisamos para avaliar a validade de nossa análise de regressão linear.
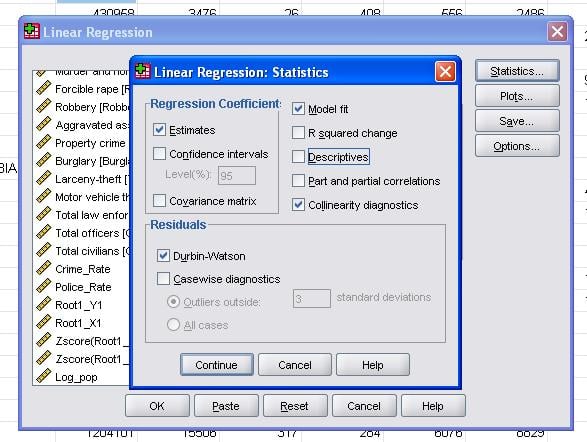
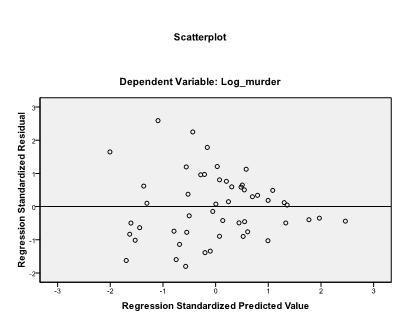
é aconselhável incluir adicionalmente o diagnóstico de colinearidade e o teste Durbin-Watson para auto-correlação. Para testar a suposição de homocedasticidade dos resíduos, também incluímos um gráfico especial no menu gráficos.
A Sintaxe SPSS para a análise de regressão linear é
REGRESSÃO
/FALTA de LISTWISE
/ESTATÍSTICAS COEF OUTS R ANOVA COLLIN TOL
/CRITÉRIOS=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENTE Log_murder
/METHOD=ENTER Log_pop
/gráfico de dispersão=(*ZRESID ,*ZPRED)
/RESÍDUOS de DURBIN HIST(ZRESID).
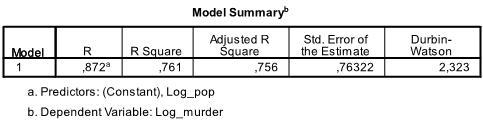
a primeira tabela da saída mostra o resumo do modelo e as estatísticas gerais de ajuste. Descobrimos que o R2 ajustado do nosso modelo é 0,756 com o R2 = .761 isso significa que a regressão linear explica 76.1% da variação nos dados. O Durbin-Watson d = 2,323, que está entre os dois valores críticos de 1,5 < d < 2,5 e, portanto, podemos supor que não há auto-correlação linear de primeira ordem nos dados.
A próxima tabela é o teste F, a regressão linear F-teste, a hipótese nula de que não há relação linear entre as duas variáveis (em outras palavras R2=0). Com F = 156.2 e 50 graus de liberdade o teste é altamente significativo, portanto, podemos supor que existe uma relação linear entre as variáveis em nosso modelo.

a tabela A seguir apresenta os coeficientes de regressão, o interceptar e a importância de todos os coeficientes e o intercepto no modelo. Descobrimos que nossa análise de regressão linear estima que a função de regressão linear seja y = -13.067 + 1.222
* X. observe que isso não se traduz em Existe 1.2 assassinatos adicionais para cada 1000 habitantes adicionais porque transformamos as variáveis.
Se nós re-correu a análise de regressão linear com as variáveis originais acabaríamos com y = 11.85 + 6.7*10-5 o que mostra que para cada 10.000 adicionais habitantes que seria de esperar para ver 6.7 adicionais assassinatos.
em nossa análise de regressão linear, o teste testa a hipótese nula de que o coeficiente é 0. O teste t descobre que tanto a interceptação quanto a variável são altamente significativas (p < 0,001) e, portanto, podemos dizer que são diferentes de zero.

esta tabela também inclui os pesos Beta (que expressam a importância relativa das variáveis independentes) e as estatísticas de colinearidade. No entanto, como temos apenas 1 variável independente em nossa análise, não prestamos atenção a esses valores.
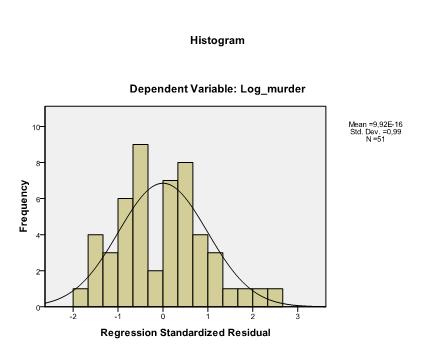
a última coisa que precisamos verificar é a homocedasticidade e a normalidade dos resíduos. O histograma indica que os resíduos se aproximam de uma distribuição normal. O Q-Q-Plot de z * pred e Z * presid nos mostra que em nossa análise de regressão linear não há tendência nos termos de erro.