laatst bijgewerkt op 31 juli 2021
hogere-orde derivaten kunnen informatie vastleggen over een functie die First-order derivaten alleen niet kunnen vastleggen.
First-order derivaten kunnen belangrijke informatie bevatten, zoals de snelheid van verandering, maar op zichzelf kunnen ze geen onderscheid maken tussen lokale minima of maxima, waar de snelheid van verandering nul is voor beide. Verscheidene optimalisatiealgoritmen pakken deze beperking aan door het gebruik van hogere-orde derivaten te benutten, zoals in Newton ‘ s methode waar de tweede-orde derivaten worden gebruikt om het lokale minimum van een optimalisatiefunctie te bereiken.
in deze tutorial zult u ontdekken hoe u univariate en multivariate derivaten met een hogere orde kunt berekenen.
na het voltooien van deze tutorial, zult u weten:
- hoe de hogere-orde derivaten van univariate functies te berekenen.
- hoe de hogere-orde derivaten van multivariate functies te berekenen.
- hoe de tweede-orde derivaten kunnen worden benut in machine learning door tweede-orde optimalisatie algoritmen.
laten we beginnen.

hogere-orde derivaten
foto door Jairph, sommige rechten voorbehouden.
Tutorial Overview
deze tutorial bestaat uit drie delen; :
- hogere-orde derivaten van univariate functies
- hogere-orde derivaten van Multivariate functies
- toepassing in Machine Learning
hogere-orde derivaten van Univariate functies
naast eerste-orde derivaten, waarvan we hebben gezien dat ze ons belangrijke informatie kunnen verschaffen over een functie, zoals de momentane snelheid van verandering, kunnen ook hogere-orde derivaten nuttig. De tweede afgeleide kan bijvoorbeeld de versnelling van een bewegend object meten, of het kan een optimalisatiealgoritme helpen onderscheid te maken tussen een lokaal maximum en een lokaal minimum.
het berekenen van hogere-orde (tweede, derde of hogere) derivaten van univariate functies is niet zo moeilijk.
de tweede afgeleide van een functie is slechts de afgeleide van zijn eerste afgeleide. De derde afgeleide is de afgeleide van de tweede afgeleide, de vierde afgeleide is de afgeleide van de derde, enzovoort.
– Page 147, Calculus for Dummies, 2016.
vandaar dat het berekenen van hogere-orde derivaten simpelweg inhoudt dat de functie herhaaldelijk wordt gedifferentieerd. Om dit te doen, kunnen we gewoon onze kennis van de macht regel toe te passen. Laten we de functie, f(x) = x3 + 2×2 – 4x + 1, als voorbeeld nemen. Vervolgens:
eerste derivaat: f ‘(x) = 3×2 + 4x – 4
tweede derivaat: f”(x) = 6x + 4
derde derivaat: f”‘(x) = 6
vierde derivaat: f (4) (x) = 0
vijfde derivaat: f (5) (x) = 0 enz.
wat we hier hebben gedaan is dat we eerst de machtregel op f(x) hebben toegepast om zijn eerste afgeleide, f'(x), vervolgens de machtregel op de eerste afgeleide hebben toegepast om de tweede te verkrijgen, enzovoort. De afgeleide zal, uiteindelijk, naar nul gaan als differentiatie herhaaldelijk wordt toegepast.
de toepassing van de product-en quotiëntregels blijft ook geldig bij het verkrijgen van derivaten van een hogere orde, maar de berekening ervan kan steeds rommeliger worden naarmate de orde toeneemt. De Algemene Leibniz-regel vereenvoudigt de taak in dit aspect, door de productregel te veralgemenen tot:
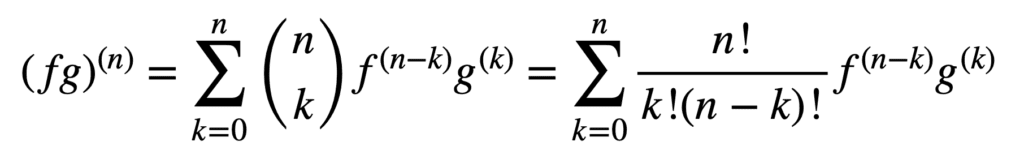
hier, de term, n! / k!(n-k)!, is de binomiale coëfficiënt uit de binomiale stelling, terwijl f (k) en g(k) de KDE afgeleide van de functies, f en G, respectievelijk aanduiden.
het vinden van de eerste en tweede derivaten (en dus het vervangen van respectievelijk n = 1 en n = 2) door de Algemene Leibniz-regel, geeft ons dus de volgende informatie::
(fg) (1) = (fg) ” = f (1) g + f g(1)
(fg) (2) = (fg)” = f (2) g + 2f (1) g(1) + f g(2)
let op het bekende eerste derivaat zoals gedefinieerd door de productregel. De Leibniz-regel kan ook worden gebruikt om hogere-orde derivaten van rationele functies te vinden, aangezien het quotiënt effectief kan worden uitgedrukt in een product van de vorm, f g-1.
hogere-orde derivaten van Multivariate functies
de definitie van hogere-orde partiële derivaten van multivariate functies is analoog aan het univariate geval: het partiële derivaat van de n-de orde voor n > 1, wordt berekend als het partiële derivaat van het (n – 1)partiële derivaat van de n-de orde. Bijvoorbeeld, het nemen van de tweede partiële afgeleide van een functie met twee variabelen resulteert in vier, tweede partiële derivaten: twee eigen partiële derivaten, fxx en fyy, en twee cross partiële derivaten, fxy en fyx.
om een “afgeleide” te nemen, moeten we een partiële afgeleide nemen met betrekking tot x of y, en er zijn vier manieren om het te doen: x dan x, x dan y, y Dan x, y Dan y.
– Page 371, Single and Multivariable Calculus, 2020.
laten we eens kijken naar de multivariate functie, f(x, y) = x2 + 3xy + 4y2, waarvoor we graag de tweede partiële afgeleiden willen vinden. Het proces begint met het vinden van de eerste-orde partiële derivaten, eerste: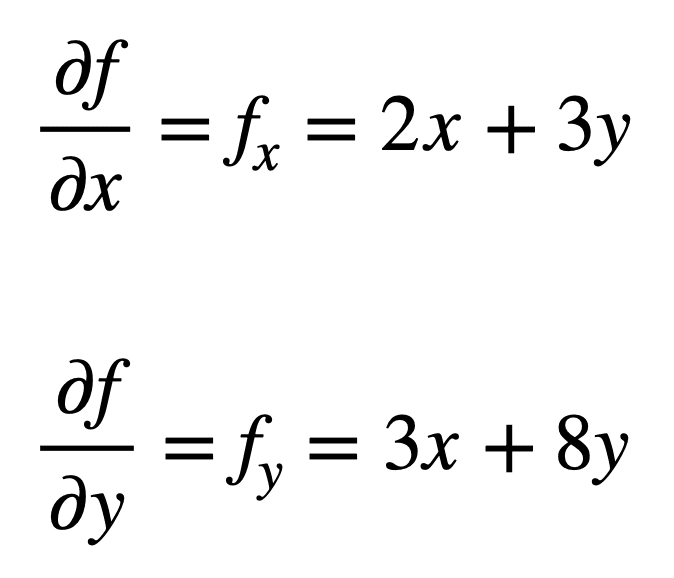
de vier, tweede-orde partiële derivaten worden dan gevonden door het proces van het vinden van de partiële derivaten, van de partiële derivaten te herhalen. De eigen partiële derivaten zijn het duidelijkst te vinden, omdat we het partiële differentiatieproces simpelweg herhalen, met betrekking tot x of y, een tweede keer:
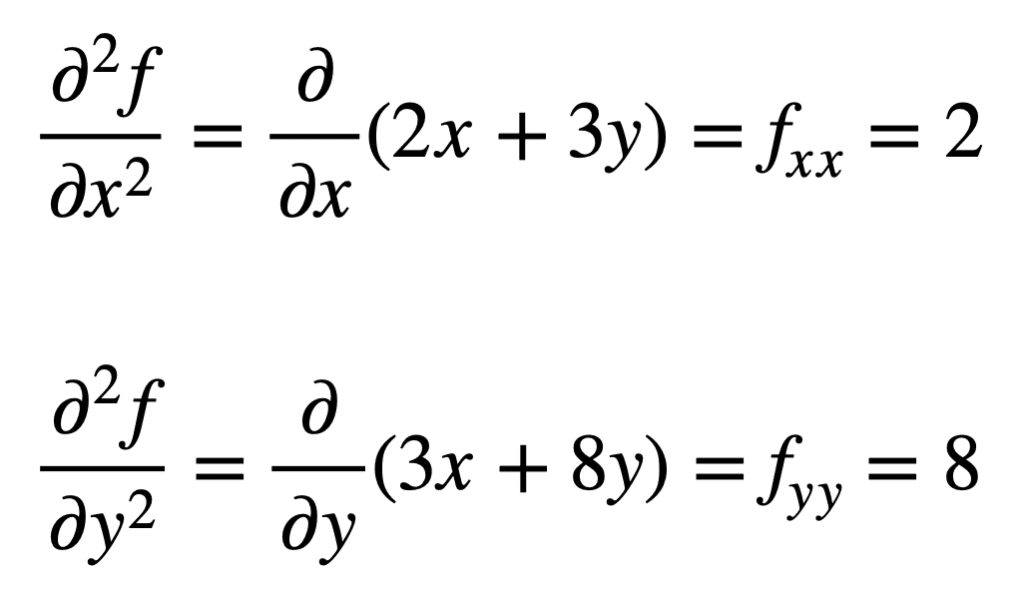
de cross partiële afgeleide van de eerder gevonden fx (dat wil zeggen, de partiële afgeleide met betrekking tot x) wordt gevonden door de partiële afgeleide van het resultaat met betrekking tot y te nemen, wat ons fxy geeft. Evenzo, het nemen van de gedeeltelijke afgeleide van fy met betrekking tot x, geeft ons fyx:
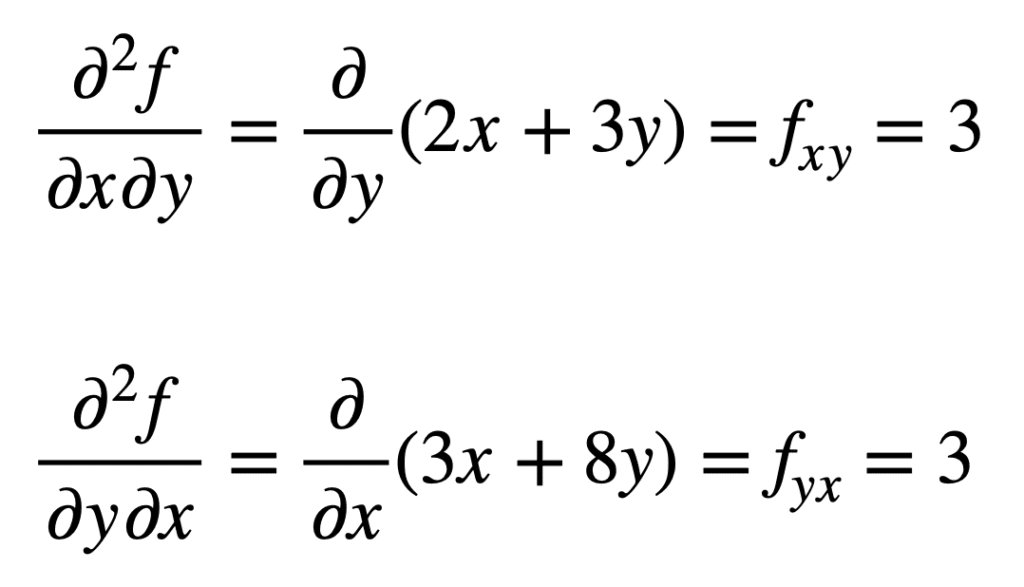
het is niet toevallig dat de cross partial derivatives hetzelfde resultaat geven. Dit wordt gedefinieerd door de stelling van Clairaut, die stelt dat zolang de kruis partiële afgeleiden continu zijn, ze gelijk zijn.
toepassing in Machine Learning
bij machine learning is het het meest gebruikte afgeleide van de tweede orde. We hadden eerder gezegd dat de tweede afgeleide ons informatie kan verschaffen die de eerste afgeleide op zichzelf niet kan vangen. Specifiek kan het ons vertellen of een kritiek punt een lokaal minimum of maximum is (gebaseerd op de vraag of de tweede afgeleide respectievelijk groter of kleiner is dan nul), waarvoor de eerste afgeleide in beide gevallen anders nul zou zijn.
er zijn verschillende tweede-orde optimalisatie-algoritmen die deze informatie gebruiken, waaronder de methode van Newton.
Second-order informatie, anderzijds, stelt ons in staat om een kwadratische benadering van de objectieve functie te maken en de juiste stapgrootte te benaderen om een lokaal minimum te bereiken …
– Page 87, Algorithms for Optimization, 2019.
in het univariate geval gebruikt Newtons methode een tweede-orde Taylorreeksuitbreiding om de kwadratische benadering uit te voeren rond een bepaald punt op de objectieve functie. De updateregel voor de methode van Newton, die wordt verkregen door de afgeleide op nul te zetten en voor de wortel op te lossen, impliceert een delingsoperatie door de tweede afgeleide. Als Newtons methode wordt uitgebreid tot multivariate optimalisatie, wordt de afgeleide vervangen door de gradiënt, terwijl de reciproque van de tweede afgeleide wordt vervangen door de inverse van de Hessische matrix.
we zullen de benaderingen van de Hessische en Taylor-serie, die gebruik maken van hogere-orde derivaten, in afzonderlijke tutorials behandelen.
verder lezen
deze sectie biedt meer informatie over het onderwerp als u dieper wilt gaan.
boeken
- enkelvoudige en multivariabele Calculus, 2020.
- Calculus for Dummies, 2016.
- Deep Learning, 2017.
- algoritmen voor optimalisatie, 2019.
samenvatting
In deze handleiding hebt u ontdekt hoe u univariate en multivariate derivaten met een hogere orde kunt berekenen.
specifiek heb je geleerd:
- hoe de hogere-orde derivaten van univariate functies te berekenen.
- hoe de hogere-orde derivaten van multivariate functies te berekenen.
- hoe de tweede-orde derivaten kunnen worden benut in machine learning door tweede-orde optimalisatie algoritmen.
