Høyere Ordens Derivater

Sist Oppdatert 31. juli 2021

høyere ordens derivater kan fange opp informasjon om en funksjon som første ordens derivater på egen hånd ikke kan fange opp.

førsteordensderivater kan fange opp viktig informasjon, for eksempel endringshastigheten, men på egen hånd kan de ikke skille mellom lokale minima eller maksima, hvor endringshastigheten er null for begge. Flere optimaliseringsalgoritmer adresserer denne begrensningen ved å utnytte bruken av høyere ordensderivater, for Eksempel I Newtons metode hvor andreordensderivater brukes til å nå det lokale minimumet av en optimaliseringsfunksjon.

i denne opplæringen vil du oppdage hvordan du beregner høyere ordens univariate og multivariate derivater.

etter å ha fullført denne opplæringen, vil du vite:

• hvordan beregne høyere ordens derivater av univariate funksjoner.
• hvordan beregne høyere ordensderivater av multivariate funksjoner.
• Hvordan andreordens derivater kan utnyttes i maskinlæring ved andreordens optimaliseringsalgoritmer.

La oss komme i gang.

Opplæringsoversikt

denne opplæringen er delt inn i tre deler; de er:

• Høyere Ordens Derivater Av Univariate Funksjoner
• Høyere Ordens Derivater Av Multivariate Funksjoner
• Søknad I Maskinlæring

Høyere Ordens Derivater Av Univariate Funksjoner

i tillegg til førsteordens derivater, som vi har sett kan gi oss viktig informasjon om en funksjon, som sin øyeblikkelige endringshastighet, kan høyere ordensderivater også være like nyttige. For eksempel kan det andre derivatet måle akselerasjonen til et bevegelige objekt, eller det kan hjelpe en optimaliseringsalgoritme å skille mellom et lokalt maksimum og et lokalt minimum.

Det Er ikke så vanskelig Å Beregne høyere rekkefølge (andre, tredje eller høyere) derivater av univariate funksjoner.

det andre derivatet av en funksjon er bare derivatet av dets første derivat. Det tredje derivatet er derivatet av det andre derivatet, det fjerde derivatet er derivatet av det tredje, og så videre.

– Side 147, Kalkulator for Dummies, 2016.

derfor innebærer beregning av høyere ordensderivater ganske enkelt å differensiere funksjonen gjentatte ganger. For å gjøre det, kan vi ganske enkelt bruke vår kunnskap om maktregelen. La oss vurdere funksjonen, f (x) = x3 + 2×2-4x + 1, som et eksempel. Deretter:

Første derivat: f'(x) = 3×2 + 4x – 4

Andre derivat: f»(x) = 6x + 4

Tredje derivat: f»‘(x) = 6

Fjerde derivat: f (4)(x) = 0

Femte derivat: f (5)(x) = 0 etc.

Det vi har gjort her er at vi først har brukt kraftregelen til f (x) for å oppnå sitt første derivat, f'(x), deretter brukt kraftregelen til det første derivatet for å oppnå det andre, og så videre. Derivatet vil til slutt gå til null når differensiering brukes gjentatte ganger.

anvendelsen av produkt-og kvotientreglene forblir også gyldig for å oppnå høyere ordensderivater, men deres beregning kan bli messier og messier når ordren øker. Den generelle Leibniz-regelen forenkler oppgaven i dette aspektet ved å generalisere produktregelen til:

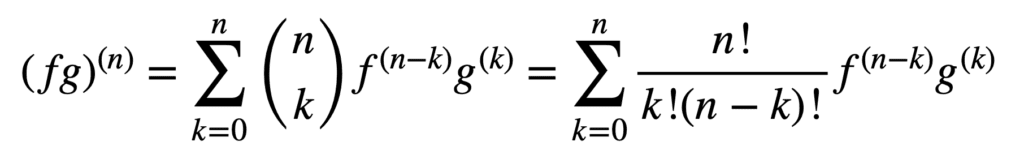
her er begrepet, n! / k!(nk)!, er binomialkoeffisienten fra binomialteoremet, mens f (k) og g(k) betegner kth-derivatet av funksjonene, henholdsvis f og g.

derfor, å finne de første og andre derivatene (og dermed erstatte n = 1 og n = 2, henholdsvis), ved den generelle Leibniz-regelen, gir oss:

(fg) (1) = (fg) ‘ = f (1) g + f g(1)

(fg) (2) = (fg)» = f (2) g + 2f(1) g(1) + f g (2)

Legg Merke til det kjente første derivatet som definert av produktregelen. Leibniz-regelen kan også brukes til å finne høyere ordensderivater av rasjonelle funksjoner, siden kvotienten effektivt kan uttrykkes i et produkt av formen, f g-1.

Høyere Ordensderivater Av Multivariate Funksjoner

definisjonen av høyere ordens partielle derivater av multivariate funksjoner er analog med univariate case: den nte ordens partielle derivat for n > 1, beregnes som det partielle derivatet av (n – 1)ordens partielle derivat. For eksempel tar det andre partielle derivatet av en funksjon med to variabler fire, andre partielle derivater: to egne partielle derivater, fxx og fyy, og to krysspartielle derivater, fxy og fyx.

For å ta et «derivat» må vi ta et delvis derivat med hensyn til x eller y, og det er fire måter å gjøre det på: x da x, x da y, y da x, y da y.

– Side 371, Single Og Multivariable Calculus, 2020.

la oss vurdere den multivariate funksjonen, f(x, y) = x2 + 3xy + 4y2, som vi ønsker å finne de andre partielle derivatene. Prosessen starter med å finne sine førsteordens partielle derivater, først: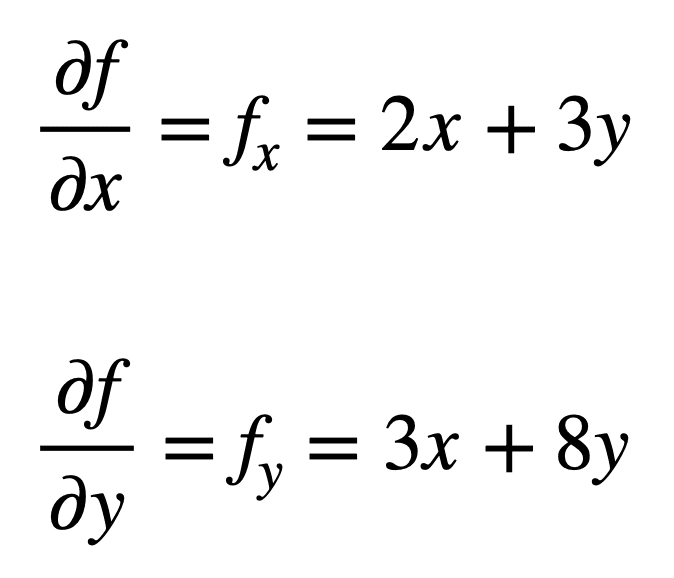

de fire andre ordens partielle derivatene blir deretter funnet ved å gjenta prosessen med å finne partielle derivater, av partielle derivater. De egne partielle derivatene er de enkleste å finne, siden vi bare gjentar partiell differensieringsprosess, med hensyn til enten x eller y, en gang til:

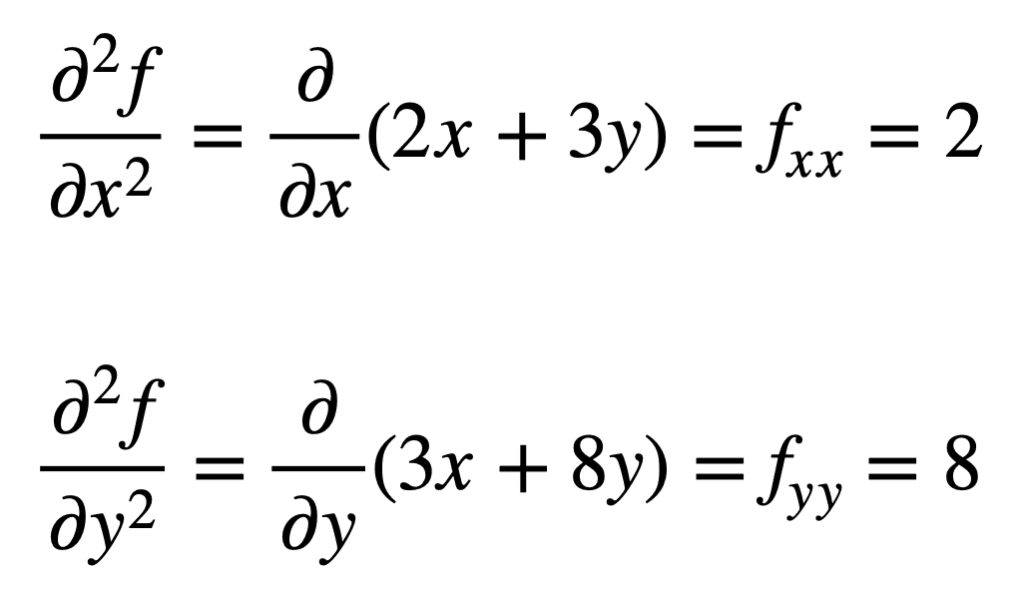
krysspartiell derivat av den tidligere funnet fx (det vil si partiell derivat med hensyn til x) er funnet ved å ta partiell derivat av resultatet med hensyn til y, noe som gir oss fxy. På samme måte gir det partielle derivatet av fy med hensyn til x, oss fyx:

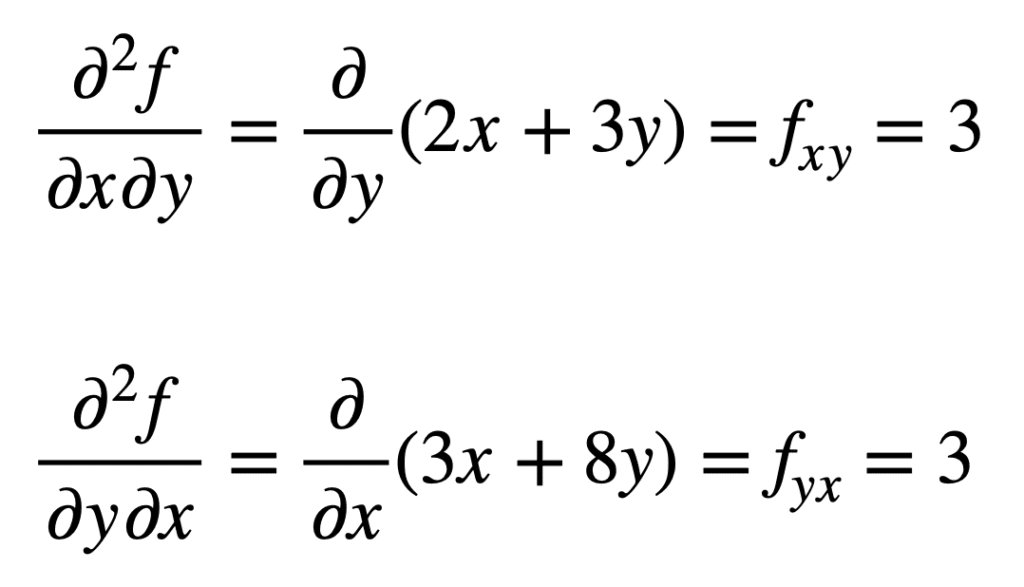
det er ikke ved et uhell at krysspartielle derivater gir det samme resultatet. Dette er definert Av Clairauts teorem, som sier at så lenge krysspartielle derivater er kontinuerlige, så er de like.

Søknad I Maskinlæring

i maskinlæring er det andreordensderivatet som mest brukes. Vi hadde tidligere nevnt at det andre derivatet kan gi oss informasjon som det første derivatet i seg selv ikke kan fange opp. Spesifikt kan det fortelle oss om et kritisk punkt er et lokalt minimum eller maksimum (basert på om det andre derivatet er større eller mindre enn null, henholdsvis), for hvilket det første derivatet ellers ville være null i begge tilfeller.

det finnes flere andre ordens optimaliseringsalgoritmer som utnytter denne informasjonen, hvorav Den ene Er Newtons metode.

Andreordsinformasjon, derimot, tillater oss å lage en kvadratisk tilnærming av objektivfunksjonen og omtrentlig riktig trinnstørrelse for å nå et lokalt minimum …

– Side 87, Algoritmer For Optimalisering, 2019.

i det univariate tilfellet bruker Newtons metode en Andreordens Taylor-serieutvidelse for å utføre den kvadratiske tilnærmingen rundt et tidspunkt på objektivfunksjonen. Oppdateringsregelen For Newtons metode, som oppnås ved å sette derivatet til null og løse for roten, innebærer en divisjonsoperasjon av det andre derivatet. Hvis Newtons metode utvides til multivariat optimalisering, erstattes derivatet med gradienten, mens gjensidig av det andre derivatet erstattes med den inverse Av Den Hessiske matrisen.

Vi skal dekke Hessiske Og Taylor-Serien tilnærminger, som utnytter bruken av høyere ordens derivater, i separate opplæringsprogrammer.

Videre Lesing

Denne delen gir flere ressurser om emnet hvis du ønsker å gå dypere.

Bøker

• Enkel Og Multivariabel Kalkulus, 2020.
• Kalkulus for Dummies, 2016.
• Dyp Læring, 2017.
• Algoritmer For Optimalisering, 2019.

Sammendrag

i denne opplæringen oppdaget du hvordan du beregner univariate og multivariate derivater med høyere rekkefølge.

spesielt lærte Du:

• hvordan beregne høyere ordens derivater av univariate funksjoner.
• hvordan beregne høyere ordensderivater av multivariate funksjoner.
• Hvordan andreordens derivater kan utnyttes i maskinlæring ved andreordens optimaliseringsalgoritmer.