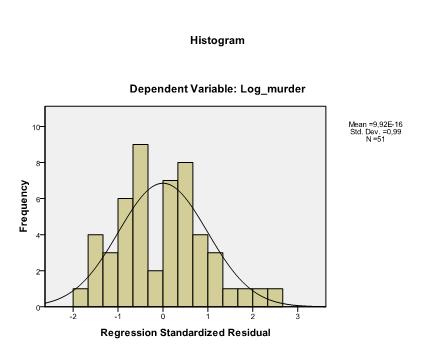
この例は、FBIの2006年の犯罪統計に基づいています。 特に、州の規模と市内の殺人事件の数との関係に興味があります。
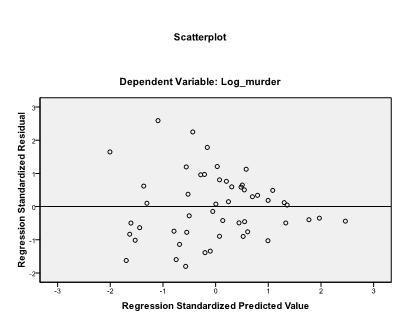
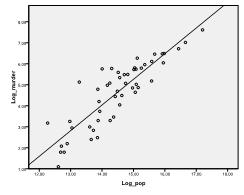
まず、データに線形関係があるかどうかを確認する必要があります。 そのために散布図をチェックします。 散布図は良好な線形関係を示し、線形回帰分析を行うことができます。 また、ピアソンの二変量相関をチェックし、両方の変数が高度に相関していることを見つけることができます(r=。959とp<0.001)。

私たちはあなたの論文の章を編集するために支援する方法を発見
理論的な枠組みを整列させ、記事を収集し、ギャップを合成し、明確な方法論とデータプランを明確にし、あなたの研究の理論的かつ実践的な意味について書くことは、私たちの包括的な論文編集サービスの一部です。
- 論文編集の専門知識を第1-5章にタイムリーにもたらします。
- すべての変更を追跡し、学術的な執筆をもたらすためにあなたと協力してください。
- 委員会のフィードバックに対処し、改訂を削減するための継続的なサポート。
次に、多変量正規性をチェックする必要があります。 この例では、多変量正規性が存在しない可能性があることがわかります。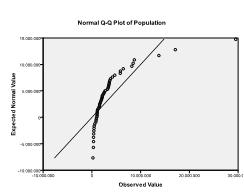
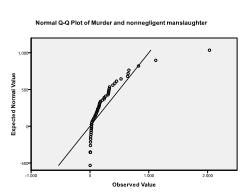
コルモゴロフ-スミルノフ検定はこの疑いを確認します(p=0.002およびp=0。006). 2つの変数に対してln変換を実行すると、問題が修正され、多変量正規性が確立されます(K-S検定p=.991とp=.543).
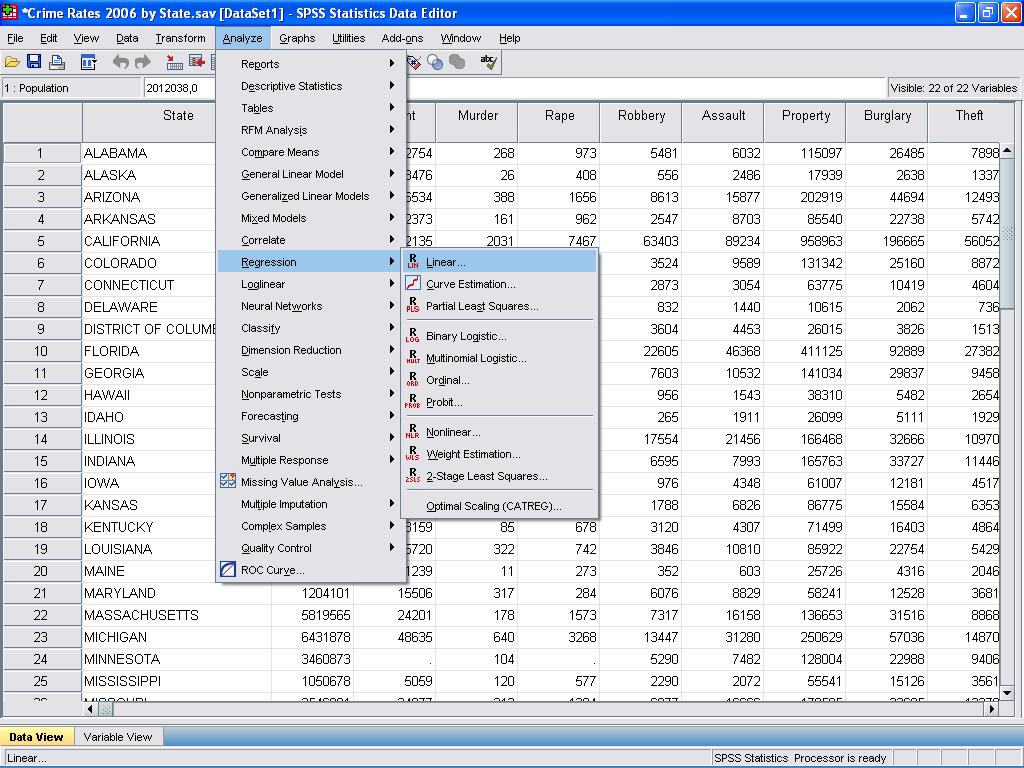
これで、線形回帰分析を行うことができます。 線形回帰は、分析/回帰/線形のSPSSにあります…
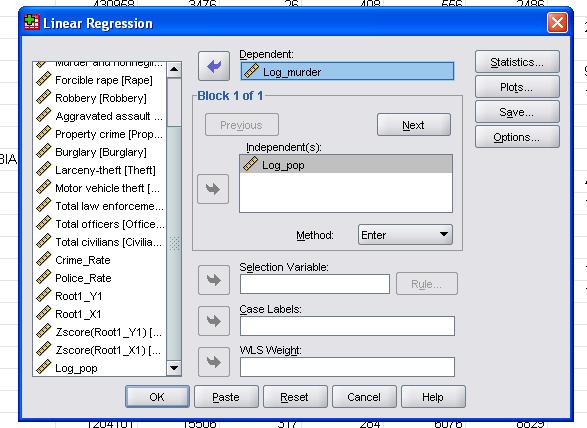
この単純なケースでは、変数log_popとlog_murderを従属変数と独立変数としてモデルに追加するだけです。
フィールド統計により、線形回帰分析の妥当性を評価するために必要な追加の統計を含めることができます。
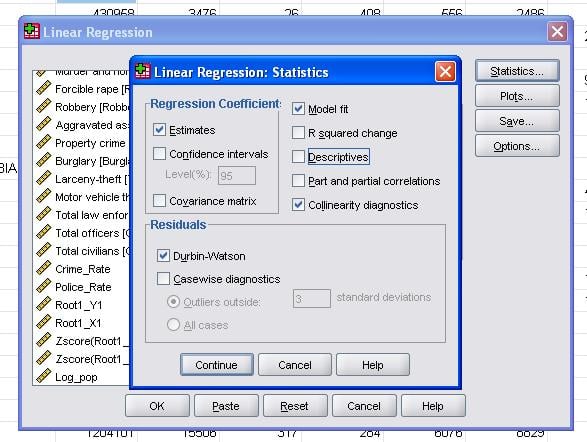
共線性診断と自己相関のためのダービン-ワトソン検定を追加で含めることをお勧めします。 残差の等分散性の仮定をテストするために、[プロット]メニューに特別なプロットも含めます。
線形回帰分析のSPSS構文は、
回帰
/リストワイズの欠落
/統計COEFF OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05)ポウト(.10)
/NOORIGIN
/従属Log_Murder
/METHOD=LOG_Popを入力します
/SCATTERPLOT=(*ZRESID,*ZPRED)
/残差DURBIN HIST(ZRESID).
出力の最初の表は、モデルの概要と全体的な適合統計量を示しています。 私たちのモデルの調整されたR2は、R2=で0.756であることがわかります。761これは、線形回帰が76を説明することを意味します。データの分散の1%。 Durbin-Watson d=2.323は、1.5<d<2.5の2つの臨界値の間にあるため、データに1次の線形自己相関がないと仮定できます。
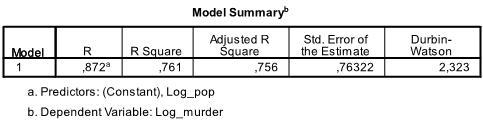
次の表はF検定で、線形回帰のF検定は2つの変数の間に線形関係がないという帰無仮説を持ちます(つまり、R2=0)。 とF=156。2自由度と50自由度この検定は非常に重要であるため、モデル内の変数間に線形関係があると仮定できます。

次の表は、回帰係数、切片、すべての係数の有意性、およびモデル内の切片を示しています。 線形回帰分析では、線形回帰関数がy=-13.067+1.222
*xと推定されていることがわかります。2人の追加殺人は1000人の追加住民ごとに発生したため、変数を変換しました。
元の変数を使用して線形回帰分析を再実行すると、y=になります11.85 + 6.7*10-5 これは、10,000人の追加の住民ごとに、6.7人の追加の殺人を見ることを期待することを示しています。
私たちの線形回帰分析では、検定は係数が0であるという帰無仮説を検定します。 T検定では、切片と変数の両方が非常に有意であることがわかります(p<0.001)ので、それらはゼロとは異なると言うかもしれません。

この表には、ベータ重み(独立変数の相対的な重要性を表す)と共線性統計も含まれています。 ただし、分析には1つの独立変数しかないため、これらの値には注意を払っていません。
最後にチェックする必要があるのは、残差の等分散性と正規性です。 ヒストグラムは、残差が正規分布に近似していることを示します。 Z*predとz*presidのQ-Q-プロットは、線形回帰分析では誤差項に傾向がないことを示しています。