Last Updated on July31,2021
高次デリバティブは、一次デリバティブ自身ではキャプチャできない関数に関する情報をキャプチャすることができます。
一次導関数は変化率などの重要な情報を取り込むことができますが、それ自体では変化率がゼロである極小値と極大値を区別することはできま いくつかの最適化アルゴリズムは、二次導関数が最適化関数の局所最小値に到達するために使用されるニュートンの方法のように、高次導関数の使用を利用することによってこの制限に対処する。
このチュートリアルでは、高次の一変量および多変量の導関数を計算する方法を発見します。
このチュートリアルを完了すると、次のことがわかります:
- 単変量関数の高次導関数を計算する方法。
- 多変量関数の高次導関数を計算する方法。
- 二次最適化アルゴリズムによる機械学習で二次導関数をどのように活用できるか。
始めましょう。

高次デリバティブ
写真:Jairph、いくつかの権利を保有。
チュートリアルの概要
このチュートリアルは三つの部分に分かれています。:
- 一変量関数の高次導関数
- 多変量関数の高次導関数
- 機械学習への応用
一変量関数の高次導関数
これまで見てきた一次導関数に加えて、関数に関する重要な情報を提供することができる。その瞬間的な変化率のように、高次の導関数も同様に有用であり得る。 たとえば、二次導関数は、移動する物体の加速度を測定したり、最適化アルゴリズムが局所的な最大値と局所的な最小値を区別するのに役立ちます。
単変量関数の高次(第二、第三、またはそれ以上)導関数を計算することはそれほど難しくありません。
関数の二次導関数は、その一次導関数の導関数にすぎません。 第三の導関数は二次導関数の導関数であり、第四の導関数は第三の導関数であり、というようになります。
–147ページ、ダミーのための微積分、2016年。
したがって、高次導関数を計算するには、単に関数を繰り返し微分する必要があります。 そのためには、べき乗則の知識を単純に適用することができます。 例として、関数f(x)=x3+2×2–4x+1を考えてみましょう。 <4181><2980>一次導関数:f’(x)=3×2+4x–4<4181><2980>二次導関数:f”(x)=6x+4<4181><2980>三次導関数:f”’(x)=6<4181><2980>四次導関数:f(4)(x)=0<4181><2980>五次導関数:f(5)(x)=0<4181><2980>0等
ここで行ったことは、まずf(x)にべき乗則を適用して一次導関数f'(x)を取得し、次に一次導関数にべき乗則を適用して二次導関数を取得するという 微分が繰り返し適用されると、微分は最終的にゼロになります。
積と商の規則の適用は、高次の導関数を得るためにも有効ですが、それらの計算は次数が増加するにつれてメシエとメシエになる可能性があります。 一般的なライプニッツ規則は、積規則を次のように一般化することによって、この側面での作業を簡素化します:
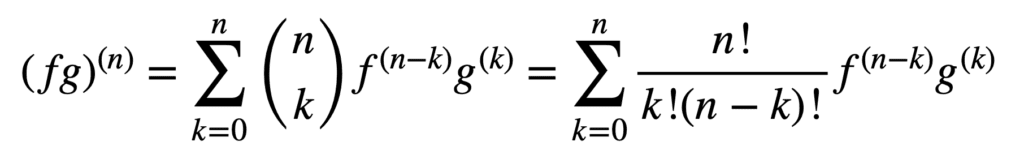
ここでは、用語、n! /k!(n-k)!,は二項定理からの二項係数であり、f(k)とg(k)はそれぞれ関数fとgのk次導関数を表します。
したがって、一般ライプニッツ則によって、第一導関数と第二導関数を見つけること(したがって、それぞれn=1とn=2を代入すること)は、次のようになり:
(fg)(1)=(fg)’=f(1)g+f g(1)
(fg)(2)=(fg)”=f(2)g+2f(1)g(1)+f g(2)
積ルールで定義されているおなじみの一次導関数に注意してください。 商はf g−1の形の積に効果的に表現できるので、ライプニッツ則は有理関数の高次導関数を見つけるためにも使用できます。
多変量関数の高次導関数
多変量関数の高次偏導関数の定義は、一変量の場合に似ています: n>1に対するn次の偏微分は、(n–1)次の偏微分の偏微分として計算されます。n>1のn次の偏微分は、(n-1)次の偏微分の偏微分として計算されます。 たとえば、2つの変数を持つ関数の2番目の偏導関数を取ると、2つの自身の偏導関数fxxとfyy、2つの交差偏導関数fxyとfyxの4つの2番目の偏導関数が得ら
“導関数”を取るには、xまたはyに関する偏導関数を取らなければならず、それを行うには四つの方法があります:x、x、x、y、y、x、y。
–Page371、Single And Multivariable Calculus、2020。
多変量関数f(x,y)=x2+3xy+4y2を考えてみましょう。 このプロセスは、最初にその一次偏導関数を見つけることから始まります: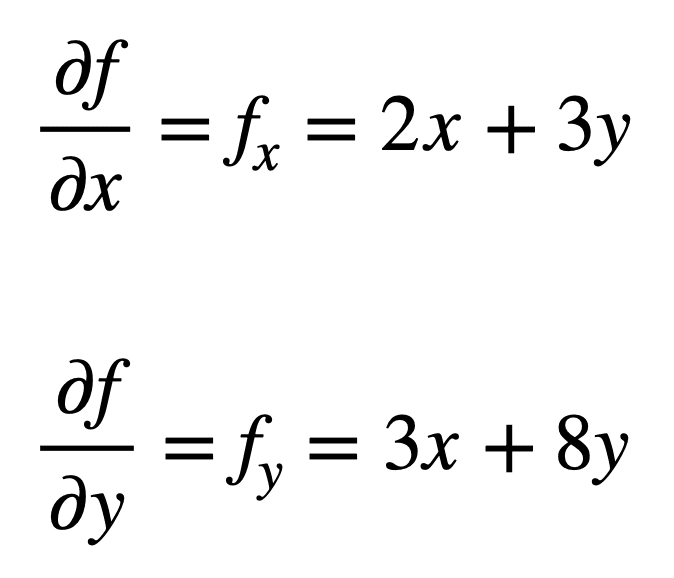
次に、偏導関数の偏導関数を求めるプロセスを繰り返すことによって、四次偏導関数が求められます。 Xまたはyのいずれかに関して偏微分プロセスを2回繰り返すだけなので、独自の偏微分は最も簡単に見つけることができます。:
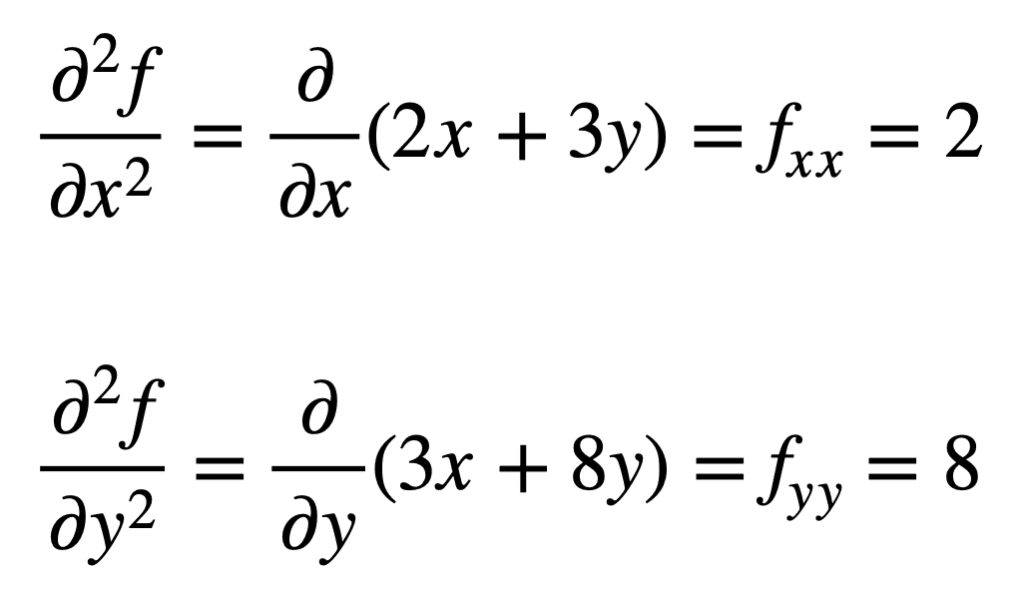
以前に見つかったfxの交差偏導関数(つまり、xに関する偏導関数)は、yに関する結果の偏導関数を取ってfxyを与えることによって求められます。 同様に、xに関するfyの偏導関数を取ると、fyxが得られます:
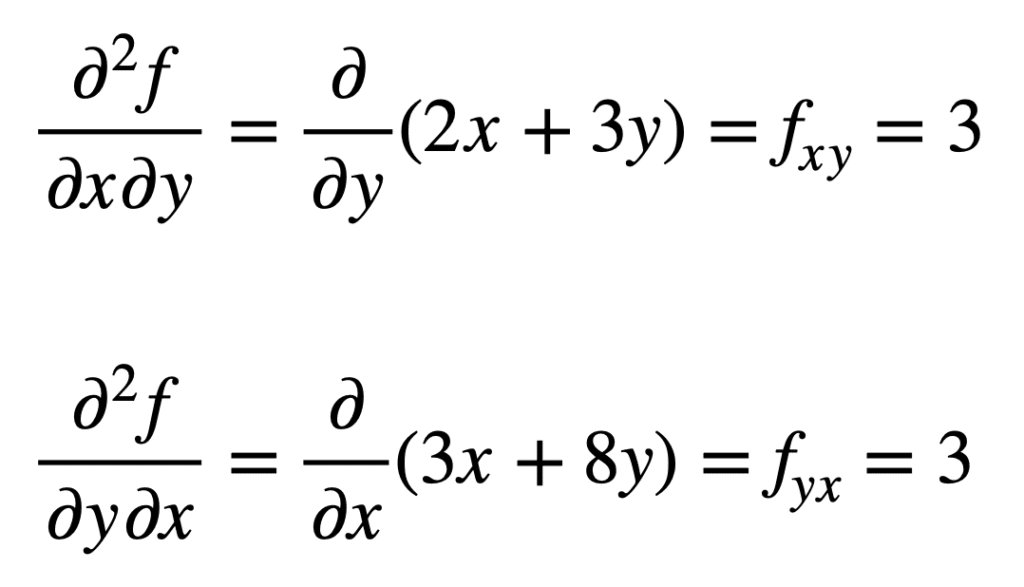
交差偏微分が同じ結果を与えるのは偶然ではありません。 これは、クロス偏微分が連続である限り、それらは等しいと述べているClairautの定理によって定義されます。
機械学習での応用
機械学習では、主に使用されるのは二次導関数です。 私たちは以前、二次導関数が一次導関数自身では捉えることができない情報を私たちに提供することができると述べました。 具体的には、臨界点が局所最小値であるか最大値であるか(二次導関数がそれぞれゼロより大きいか小さいかに基づいて)、一次導関数がそうでなければ、両方の場合においてゼロであるかどうかを知ることができる。
この情報を利用するいくつかの二次最適化アルゴリズムがあり、そのうちの一つはニュートンの方法です。
一方、二次情報は、目的関数の二次近似を行い、局所最小値に達するように正しいステップサイズを近似することを可能にする…
-ページ87、最適化のためのアルゴリズム、2019。
一変量の場合、ニュートン法は二次テイラー級数展開を使用して、目的関数上のある点の周りで二次近似を実行します。 ニュートン法の更新規則は、導関数をゼロに設定し、根を解くことによって得られ、二次導関数による除算が含まれます。 ニュートン法を多変量最適化に拡張すると、導関数は勾配に置き換えられ、二次導関数の逆数はヘッセ行列の逆数に置き換えられます。
高次導関数の使用を活用したヘッセ級数近似とテイラー級数近似については、個別のチュートリアルで説明します。
さらに読む
このセクションでは、より深く行くために探している場合は、トピックに関するより多くのリソースを提供します。
Books
- Single And Multivariable Calculus,2020.
- ダミーのための微積分,2016.
- ディープラーニング、2017年。
- 最適化のためのアルゴリズム、2019年。
概要
このチュートリアルでは、高次の一変量および多変量の導関数を計算する方法を発見しました。
:
- 単変量関数の高次導関数を計算する方法。
- 多変量関数の高次導関数を計算する方法。
- 二次最適化アルゴリズムによる機械学習で二次導関数をどのように活用できるか。
