Questo esempio si basa sulle statistiche sulla criminalità dell’FBI del 2006. In particolare siamo interessati alla relazione tra le dimensioni dello stato e il numero di omicidi in città.
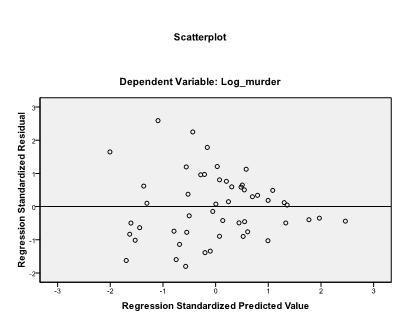
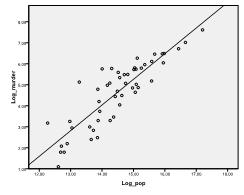
Per prima cosa dobbiamo verificare se esiste una relazione lineare nei dati. Per questo controlliamo il grafico a dispersione. Il grafico a dispersione indica una buona relazione lineare, che ci consente di condurre un’analisi di regressione lineare. Possiamo anche controllare la correlazione bivariata di Pearson e scoprire che entrambe le variabili sono altamente correlate (r = .959 con p < 0,001).

Scopri come aiutiamo a modificare i capitoli della tua tesi
Allineare il quadro teorico, raccogliere articoli, sintetizzare lacune, articolare una metodologia chiara e un piano dati e scrivere sulle implicazioni teoriche e pratiche della tua ricerca fanno parte dei nostri servizi completi di editing della tesi.
- Portare tesi di editing competenze ai capitoli 1-5 in modo tempestivo.
- Tieni traccia di tutte le modifiche, quindi lavora con te per realizzare la scrittura accademica.
- Supporto continuo per affrontare il feedback del comitato, riducendo le revisioni.
In secondo luogo dobbiamo verificare la normalità multivariata. Nel nostro esempio troviamo che la normalità multivariata potrebbe non essere presente.
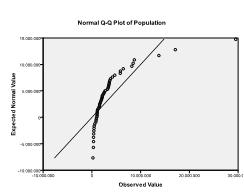
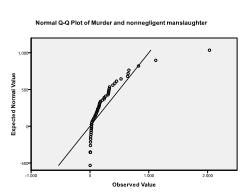
Il test Kolmogorov-Smirnov conferma questo sospetto (p = 0,002 e p = 0.006). Condurre una trasformazione ln sulle due variabili risolve il problema e stabilisce la normalità multivariata (K-S test p = .991 e p = .543).
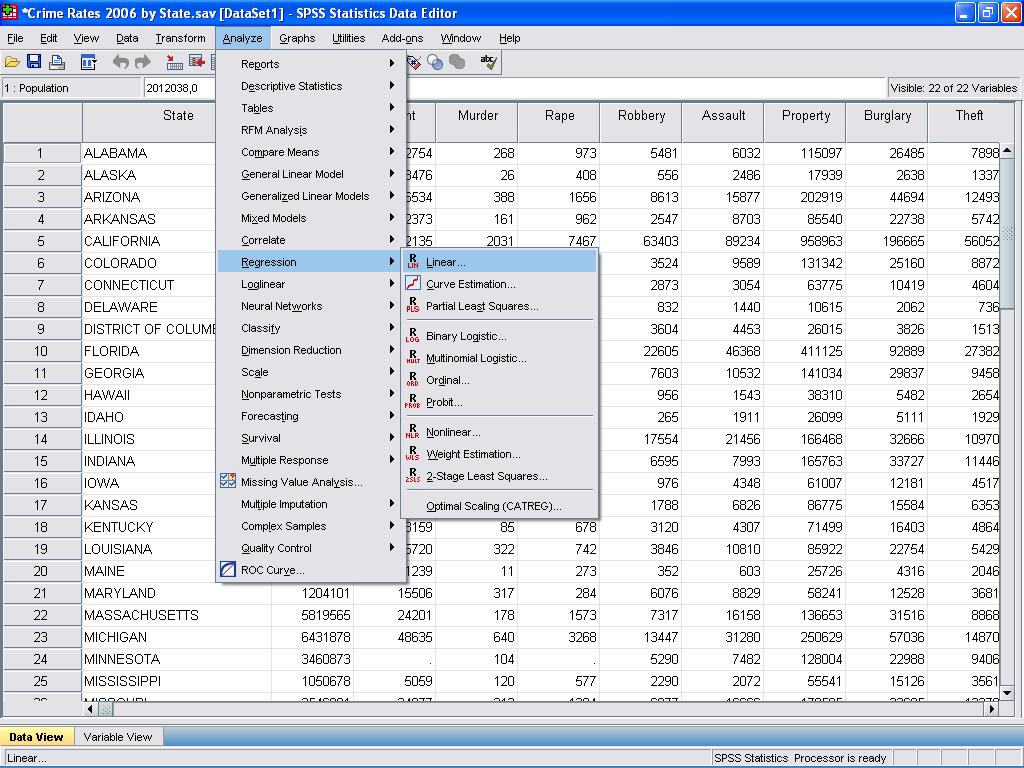
Ora possiamo condurre l’analisi di regressione lineare. La regressione lineare si trova in SPSS in Analyze / Regression / Linear…
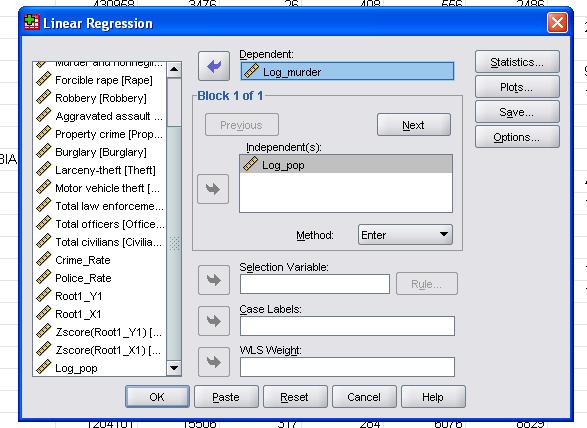
In questo semplice caso dobbiamo semplicemente aggiungere le variabili log_pop e log_murder al modello come variabili dipendenti e indipendenti.
Le statistiche sul campo ci consentono di includere statistiche aggiuntive che ci servono per valutare la validità della nostra analisi di regressione lineare.
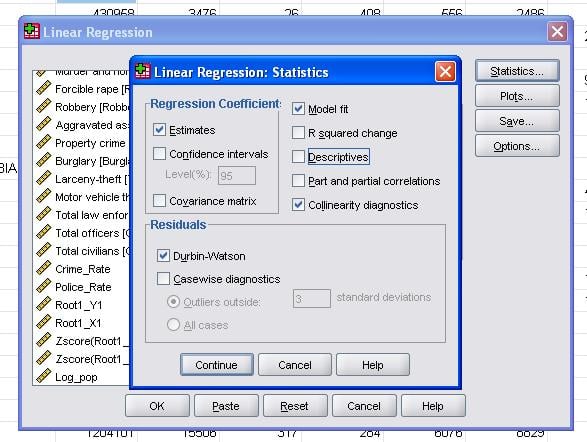
Si consiglia di includere anche la diagnostica collinearità e il test Durbin-Watson per l’auto-correlazione. Per testare l’assunzione di omoscedasticità dei residui includiamo anche una trama speciale nel menu Trame.
La sintassi SPSS per l’analisi di regressione lineare è
REGRESSIONE
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) BRONCIO(.10)
/NOORIGIN
/Log_murder DIPENDENTE
/METHOD=INSERISCI Log_pop
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS DURBIN HIST(ZRESID).
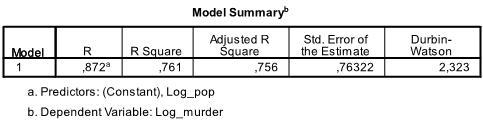
La prima tabella dell’output mostra il riepilogo del modello e le statistiche generali di adattamento. Troviamo che la R2 regolata del nostro modello è 0.756 con la R2 = .761 ciò significa che la regressione lineare spiega 76.1% della varianza nei dati. Il Durbin-Watson d = 2.323, che è tra i due valori critici di 1.5 < d < 2.5 e quindi possiamo supporre che non ci sia un’auto-correlazione lineare del primo ordine nei dati.
La tabella successiva è il test F, il test F della regressione lineare ha l’ipotesi nulla che non vi sia alcuna relazione lineare tra le due variabili (in altre parole R2=0). Con F = 156.2 e 50 gradi di libertà il test è altamente significativo, quindi possiamo supporre che ci sia una relazione lineare tra le variabili nel nostro modello.

La tabella successiva mostra i coefficienti di regressione, l’intercetta e il significato di tutti i coefficienti e l’intercetta del modello. Troviamo che la nostra analisi di regressione lineare stima che la funzione di regressione lineare sia y = -13.067 + 1.222
* x. Si prega di notare che questo non si traduce in c’è 1.2 omicidi aggiuntivi per ogni 1000 abitanti aggiuntivi perché abbiamo trasformato le variabili.
Se rieseguissimo l’analisi di regressione lineare con le variabili originali finiremmo con y = 11.85 + 6.7*10-5 il che dimostra che per ogni 10.000 abitanti aggiuntivi ci aspetteremmo di vedere 6,7 omicidi aggiuntivi.
Nella nostra analisi di regressione lineare il test verifica l’ipotesi nulla che il coefficiente sia 0. Il t-test rileva che sia intercept che variable sono altamente significativi (p < 0.001) e quindi potremmo dire che sono diversi da zero.

Questa tabella include anche i pesi Beta (che esprimono l’importanza relativa delle variabili indipendenti) e le statistiche di collinearità. Tuttavia, poiché abbiamo solo 1 variabile indipendente nella nostra analisi, non prestiamo attenzione a quei valori.
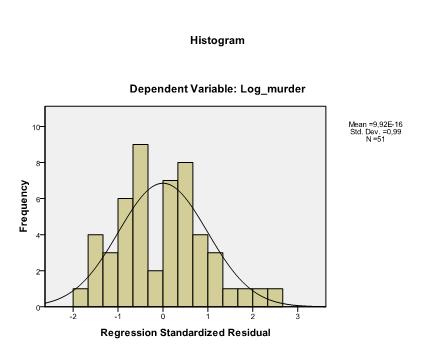
L’ultima cosa che dobbiamo controllare è l’omoscedasticità e la normalità dei residui. L’istogramma indica che i residui approssimano una distribuzione normale. Il Q-Q-Plot di z * pred e z * presid ci mostra che nella nostra analisi di regressione lineare non c’è tendenza nei termini di errore.