Derivados de orden superior

Última actualización el 31 de julio de 2021

Los derivados de orden superior pueden capturar información sobre una función que los derivados de primer orden por sí solos no pueden capturar.

Los derivados de primer orden pueden capturar información importante, como la tasa de cambio, pero por sí solos no pueden distinguir entre mínimos o máximos locales, donde la tasa de cambio es cero para ambos. Varios algoritmos de optimización abordan esta limitación explotando el uso de derivadas de orden superior, como en el método de Newton, donde las derivadas de segundo orden se utilizan para alcanzar el mínimo local de una función de optimización.

En este tutorial, descubrirá cómo calcular derivados univariados y multivariados de orden superior.

Después de completar este tutorial, sabrá:

• Cómo calcular las derivadas de orden superior de funciones univariadas.
• Cómo calcular las derivadas de orden superior de funciones multivariantes.
• Cómo se pueden explotar los derivados de segundo orden en el aprendizaje automático mediante algoritmos de optimización de segundo orden.

Comencemos.

Descripción general del tutorial

Este tutorial se divide en tres partes::

• Derivados de Funciones Univariadas de Orden Superior
• Derivados de Funciones Multivariadas de Orden Superior
• Aplicación en Aprendizaje automático

Derivados de Funciones Univariadas de Orden superior

Además de derivados de primer orden, que hemos visto pueden proporcionarnos información importante sobre una función, como su tasa de cambio instantánea, los derivados de orden superior también pueden ser igualmente útiles. Por ejemplo, la segunda derivada puede medir la aceleración de un objeto en movimiento, o puede ayudar a un algoritmo de optimización a distinguir entre un máximo local y un mínimo local.

Calcular derivadas de orden superior (segunda, tercera o superior) de funciones univariadas no es tan difícil.

La segunda derivada de una función es la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, la cuarta derivada es la derivada de la tercera, y así sucesivamente.

– Página 147, Cálculo para Maniquíes, 2016.

Por lo tanto, calcular derivadas de orden superior simplemente implica diferenciar la función repetidamente. Para hacerlo, simplemente podemos aplicar nuestro conocimiento de la regla del poder. Consideremos la función, f ( x) = x3 + 2×2 – 4x + 1, como ejemplo. Entonces:

Primera derivada: f'(x) = 3×2 + 4x – 4

Segunda derivada: f»(x) = 6x + 4

Tercera derivada: f»‘(x) = 6

Cuarta derivada: f (4)(x) = 0

Quinta derivada: f (5)(x) = 0, etc.

Lo que hemos hecho aquí es que primero aplicamos la regla de potencia a f (x) para obtener su primera derivada, f'(x), luego aplicamos la regla de potencia a la primera derivada para obtener la segunda, y así sucesivamente. La derivada, eventualmente, irá a cero a medida que la diferenciación se aplique repetidamente.

La aplicación de las reglas de producto y cociente también sigue siendo válida para obtener derivados de orden superior, pero su cálculo puede volverse más desordenado a medida que aumenta el orden. La regla general de Leibniz simplifica la tarea en este aspecto, al generalizar la regla del producto para:

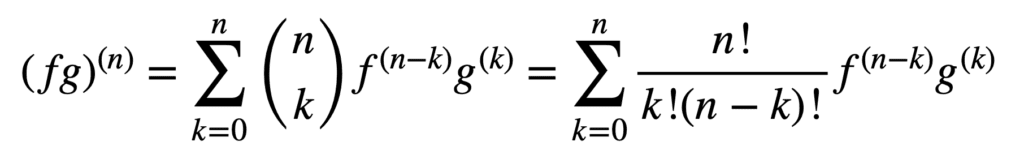
Aquí, el término, n! / k!(n-k)!, es el coeficiente binomial del teorema binomial, mientras que f (k) y g(k) denotan la k-ésima derivada de las funciones, f y g, respectivamente.

Por lo tanto, encontrar la primera y segunda derivadas (y, por lo tanto, sustituir n = 1 y n = 2, respectivamente), por la regla general de Leibniz, nos da:

(fg)(1) = (fg)’ = f (1) g + f g(1)

(fg)(2) = (fg)» = f (2) g + 2f (1) g(1) + f g(2)

Aviso de lo familiar de primera derivada definida por el producto de la regla. La regla de Leibniz también se puede usar para encontrar derivadas de orden superior de funciones racionales, ya que el cociente se puede expresar efectivamente en un producto de la forma, f g-1.

Derivadas de orden superior de Funciones Multivariantes

La definición de derivadas parciales de orden superior de funciones multivariantes es análoga al caso univariante: la derivada parcial de orden n para n > 1, se calcula como la derivada parcial de la derivada parcial de orden n – 1. Por ejemplo, tomar la segunda derivada parcial de una función con dos variables da como resultado cuatro segundas derivadas parciales: dos derivadas parciales propias, fxx y fyy, y dos derivadas parciales cruzadas, fxy y fyx.

Para tomar una «derivada», debemos tomar una derivada parcial con respecto a x o y, y hay cuatro formas de hacerlo: x luego x, x luego y, y luego x, y luego y.

– Página 371, Cálculo simple y Multivariable, 2020.

Consideremos la función multivariante, f ( x, y) = x2 + 3xy + 4y2, para la que nos gustaría encontrar las segundas derivadas parciales. El proceso comienza con la búsqueda de sus derivadas parciales de primer orden, primero: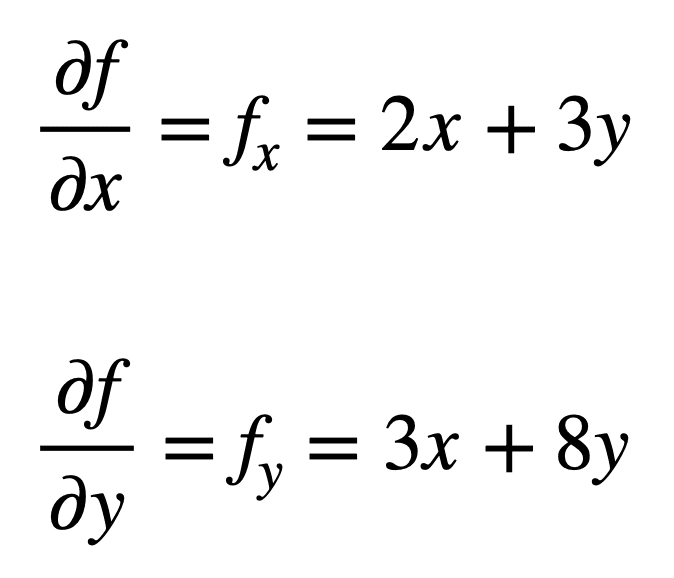

Las cuatro derivadas parciales de segundo orden se encuentran repitiendo el proceso de encontrar las derivadas parciales de las derivadas parciales. Las derivadas parciales propias son las más sencillas de encontrar, ya que simplemente repetimos el proceso de diferenciación parcial, con respecto a x o y, una segunda vez:

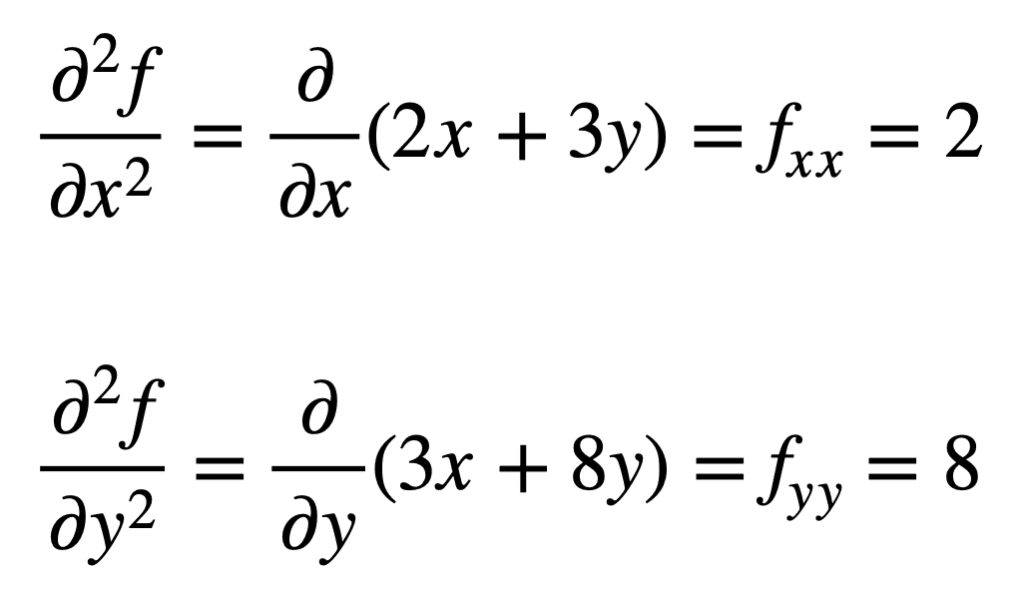
La derivada parcial cruzada del fx encontrado previamente (es decir, la derivada parcial con respecto a x) se encuentra tomando la derivada parcial del resultado con respecto a y, dándonos fxy. Del mismo modo, tomando la derivada parcial de fy con respecto a x, nos da fyx:

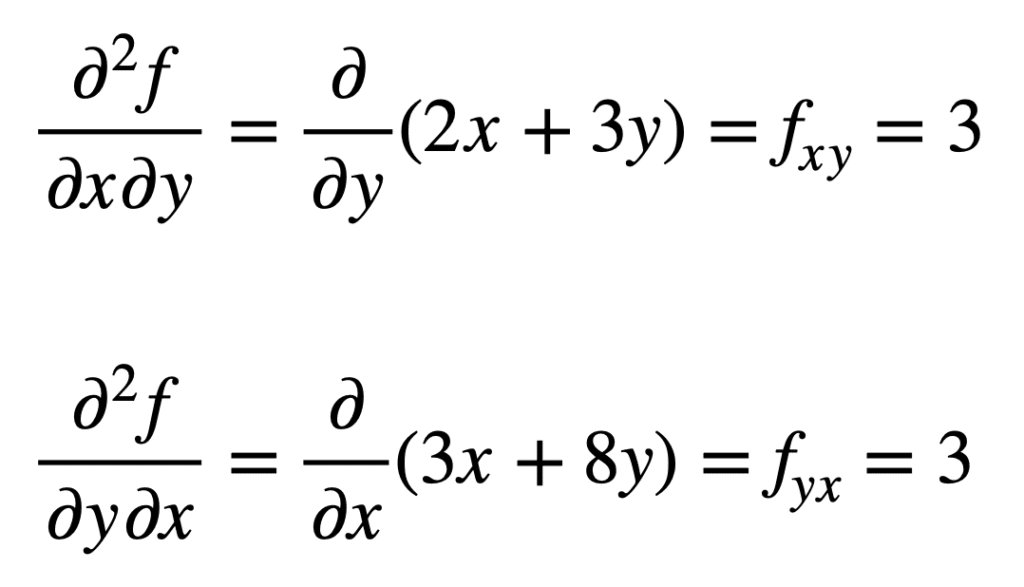
No es por accidente que las derivadas parciales cruzadas den el mismo resultado. Esto se define por el teorema de Clairaut, que establece que mientras las derivadas parciales cruzadas sean continuas, entonces son iguales.

Aplicación en Aprendizaje automático

En aprendizaje automático, es el derivado de segundo orden que se usa principalmente. Habíamos mencionado anteriormente que la segunda derivada puede proporcionarnos información que la primera derivada por sí sola no puede capturar. Específicamente, puede decirnos si un punto crítico es un mínimo o un máximo local (basado en si la segunda derivada es mayor o menor que cero, respectivamente), para lo cual la primera derivada, de lo contrario, sería cero en ambos casos.

Hay varios algoritmos de optimización de segundo orden que aprovechan esta información, uno de los cuales es el método de Newton.

La información de segundo orden, por otro lado, nos permite hacer una aproximación cuadrática de la función objetivo y aproximar el tamaño de paso correcto para alcanzar un mínimo local

– Página 87, Algoritmos para Optimización, 2019.

En el caso univariado, el método de Newton utiliza una expansión de serie de Taylor de segundo orden para realizar la aproximación cuadrática alrededor de algún punto de la función objetiva. La regla de actualización para el método de Newton, que se obtiene estableciendo la derivada a cero y resolviendo para la raíz, implica una operación de división por la segunda derivada. Si el método de Newton se extiende a la optimización multivariante, la derivada se reemplaza por el gradiente, mientras que el recíproco de la segunda derivada se reemplaza por el inverso de la matriz de Hessian.

Cubriremos las aproximaciones de las series de Hessian y Taylor, que aprovechan el uso de derivadas de orden superior, en tutoriales separados.

Más información

Esta sección proporciona más recursos sobre el tema si desea profundizar más.

Libros

• Cálculo único y Multivariable, 2020.
• Cálculo para Maniquíes, 2016.
• Aprendizaje profundo, 2017.
• Algoritmos para Optimización, 2019.

Resumen

En este tutorial, descubriste cómo calcular derivadas univariadas y multivariadas de orden superior.

Específicamente, aprendiste:

• Cómo calcular las derivadas de orden superior de funciones univariadas.
• Cómo calcular las derivadas de orden superior de funciones multivariantes.
• Cómo se pueden explotar los derivados de segundo orden en el aprendizaje automático mediante algoritmos de optimización de segundo orden.