Dieses Beispiel basiert auf der Kriminalstatistik des FBI von 2006. Besonders interessiert uns das Verhältnis zwischen der Größe des Staates und der Anzahl der Morde in der Stadt.
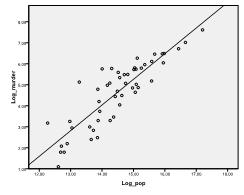
Zuerst müssen wir prüfen, ob es eine lineare Beziehung in den Daten gibt. Dafür überprüfen wir das Streudiagramm. Das Streudiagramm zeigt eine gute lineare Beziehung an, die es uns ermöglicht, eine lineare Regressionsanalyse durchzuführen. Wir können auch die bivariate Korrelation von Pearson überprüfen und feststellen, dass beide Variablen stark korreliert sind (r = .959 mit p < 0,001).

Entdecken Sie, wie wir Ihnen helfen, Ihre Dissertationskapitel zu bearbeiten
Das Ausrichten des theoretischen Rahmens, das Sammeln von Artikeln, das Synthetisieren von Lücken, das Artikulieren einer klaren Methodik und eines Datenplans sowie das Schreiben über die theoretischen und praktischen Implikationen Ihrer Forschung sind Teil unserer umfassenden Dissertationsbearbeitung.
- Bringen Dissertation Bearbeitung Know-how zu den Kapiteln 1-5 rechtzeitig.
- Verfolgen Sie alle Änderungen und arbeiten Sie dann mit Ihnen zusammen, um wissenschaftliches Schreiben zu erreichen.
- Laufende Unterstützung, um das Feedback des Ausschusses zu berücksichtigen und Revisionen zu reduzieren.
Zweitens müssen wir nach multivariater Normalität suchen. In unserem Beispiel finden wir, dass multivariate Normalität möglicherweise nicht vorhanden ist.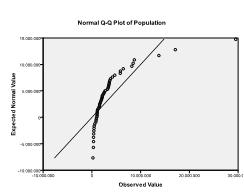
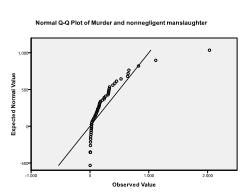
Der Kolmogorov-Smirnov-Test bestätigt diesen Verdacht (p = 0,002 und p = 0.006). Die Durchführung einer ln-Transformation an den beiden Variablen behebt das Problem und stellt die multivariate Normalität her (K-S-p = .991 und p = .543).
Wir können nun die lineare Regressionsanalyse durchführen. Die lineare Regression findet sich in SPSS in Analyze/Regression/Linear…
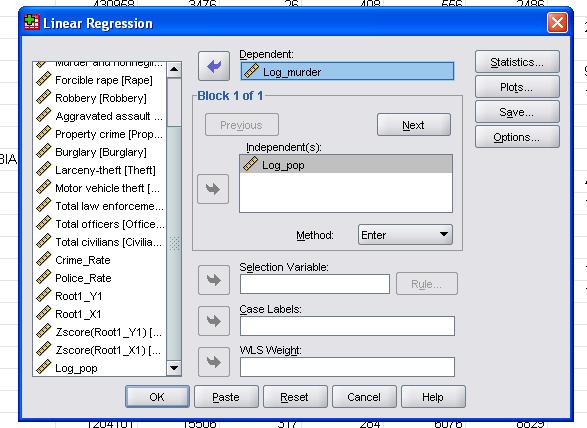
In diesem einfachen Fall müssen wir nur die Variablen log_pop und log_murder als abhängige und unabhängige Variablen zum Modell hinzufügen.
Das Feld Statistik ermöglicht es uns, zusätzliche Statistiken aufzunehmen, die wir benötigen, um die Validität unserer linearen Regressionsanalyse zu bewerten.
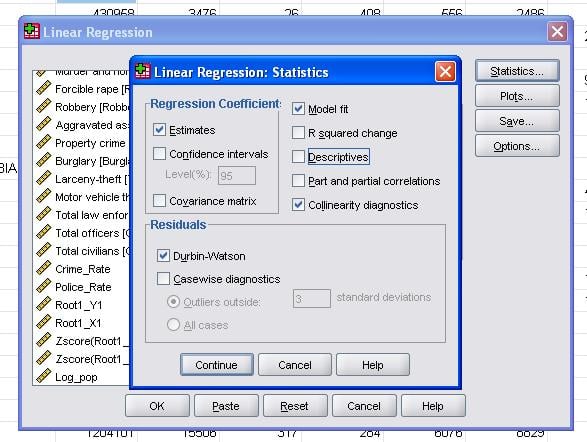
Es empfiehlt sich, zusätzlich die Kollinearitätsdiagnostik und den Durbin-Watson-Test zur Autokorrelation einzubeziehen. Um die Annahme der Homoskedastizität von Residuen zu testen, fügen wir auch ein spezielles Diagramm in das Menü Diagramme ein.
Die SPSS-Syntax für die lineare Regressionsanalyse lautet
REGRESSION
/FEHLENDE LISTE
/STATISTICS COEFFICIENT R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) SCHMOLLEN(.10)
/NOORIGIN
/ ABHÄNGIGER Log_murder
/ METHODE= Log_pop EINGEBEN
/ STREUDIAGRAMM=(*ZRESID , *ZPRED)
/RESIDUEN DURBIN HIST(ZRESID).
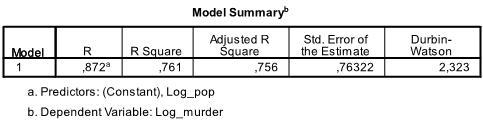
Die erste Tabelle der Ausgabe zeigt die Modellzusammenfassung und die Gesamtanpassungsstatistik. Wir finden, dass das angepasste R2 unseres Modells 0,756 mit dem R2 = ist.761 das bedeutet, dass die lineare Regression erklärt 76.1% der Varianz in den Daten. Die Durbin-Watson d = 2.323, die zwischen den beiden kritischen Werten von 1.5 < d < 2.5 liegt und daher können wir davon ausgehen, dass es keine lineare Autokorrelation erster Ordnung in den Daten gibt.
Die nächste Tabelle ist der F-Test, der F-Test der linearen Regression hat die Nullhypothese, dass es keine lineare Beziehung zwischen den beiden Variablen gibt (mit anderen Worten R2 =0). Mit F = 156.2 und 50 Freiheitsgrade der Test ist hoch signifikant, daher können wir davon ausgehen, dass es eine lineare Beziehung zwischen den Variablen in unserem Modell gibt.

Die folgende Tabelle zeigt die Regressionskoeffizienten, den Achsenabschnitt und die Signifikanz aller Koeffizienten und den Achsenabschnitt im Modell. Wir finden, dass unsere lineare Regressionsanalyse die lineare Regressionsfunktion auf y = -13.067 + 1.222
* x schätzt. Bitte beachten Sie, dass dies nicht in there is 1 übersetzt wird.2 zusätzliche Morde pro 1000 zusätzliche Einwohner, weil wir die Variablen transformiert haben.
Wenn wir die lineare Regressionsanalyse mit den ursprünglichen Variablen erneut ausführen würden, würden wir mit y = 11.85 + 6.7*10-5 was zeigt, dass wir auf 10.000 zusätzliche Einwohner 6,7 zusätzliche Morde erwarten würden.
In unserer linearen Regressionsanalyse testet der Test die Nullhypothese, dass der Koeffizient 0 ist. Der t-Test stellt fest, dass sowohl Intercept als auch Variable hoch signifikant sind (p < 0,001) und wir könnten daher sagen, dass sie sich von Null unterscheiden.

Diese Tabelle enthält auch die Beta-Gewichte (die die relative Bedeutung unabhängiger Variablen ausdrücken) und die Kollinearitätsstatistik. Da wir jedoch nur 1 unabhängige Variable in unserer Analyse haben, achten wir nicht auf diese Werte.
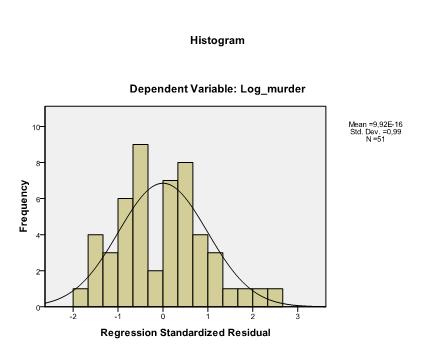
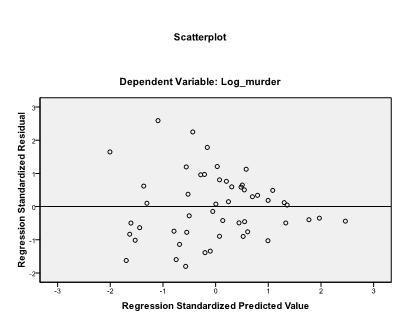
Das letzte, was wir überprüfen müssen, ist die Homoskedastizität und Normalität der Residuen. Das Histogramm zeigt an, dass sich die Residuen einer Normalverteilung annähern. Das Q-Q-Diagramm von z * pred und z * presid zeigt uns, dass es in unserer linearen Regressionsanalyse keine Tendenz in den Fehlertermen gibt.