Zuletzt aktualisiert am 31.Juli 2021
Derivate höherer Ordnung können Informationen über eine Funktion erfassen, die Derivate erster Ordnung allein nicht erfassen können.
Ableitungen erster Ordnung können wichtige Informationen wie die Änderungsrate erfassen, können jedoch allein nicht zwischen lokalen Minima oder Maxima unterscheiden, wobei die Änderungsrate für beide Null ist. Mehrere Optimierungsalgorithmen adressieren diese Einschränkung, indem sie die Verwendung von Ableitungen höherer Ordnung ausnutzen, wie in Newtons Methode, wo die Ableitungen zweiter Ordnung verwendet werden, um das lokale Minimum einer Optimierungsfunktion zu erreichen.
In diesem Tutorial erfahren Sie, wie Sie univariate und multivariate Ableitungen höherer Ordnung berechnen.
Nach Abschluss dieses Tutorials werden Sie wissen:
- Wie man die Ableitungen höherer Ordnung von univariaten Funktionen berechnet.
- Wie man die Ableitungen höherer Ordnung von multivariaten Funktionen berechnet.
- Wie die Ableitungen zweiter Ordnung im maschinellen Lernen durch Optimierungsalgorithmen zweiter Ordnung ausgenutzt werden können.
Lass uns anfangen.

Higher-Order Derivatives
Foto von Jairph, einige Rechte vorbehalten.
Tutorial Übersicht
Dieses Tutorial ist in drei Teile gegliedert; sie sind:
- Ableitungen höherer Ordnung von univariaten Funktionen
- Ableitungen höherer Ordnung von multivariaten Funktionen
- Anwendung im maschinellen Lernen
Ableitungen höherer Ordnung von univariaten Funktionen
Zusätzlich zu Ableitungen erster Ordnung, die wir gesehen haben, können uns wichtige Informationen über eine Funktion , wie seine momentane Änderungsrate, Ableitungen höherer Ordnung können ebenfalls gleichermaßen nützlich sein. Beispielsweise kann die zweite Ableitung die Beschleunigung eines sich bewegenden Objekts messen oder einem Optimierungsalgorithmus helfen, zwischen einem lokalen Maximum und einem lokalen Minimum zu unterscheiden.
Die Berechnung von Ableitungen höherer Ordnung (zweite, dritte oder höhere) von univariaten Funktionen ist nicht so schwierig.
Die zweite Ableitung einer Funktion ist nur die Ableitung ihrer ersten Ableitung. Die dritte Ableitung ist die Ableitung der zweiten Ableitung, die vierte Ableitung ist die Ableitung der dritten und so weiter.
– Seite 147, Calculus für Dummies, 2016.
Daher beinhaltet das Berechnen von Ableitungen höherer Ordnung einfach die wiederholte Differenzierung der Funktion. Um dies zu tun, können wir einfach unser Wissen über die Machtregel anwenden. Betrachten wir als Beispiel die Funktion f(x) = x3 + 2×2 – 4x + 1. Dann:
Erste Ableitung: f'(x) = 3×2 + 4x – 4
Zweite Ableitung: f“(x) = 6x + 4
Dritte Ableitung: f“‚(x) = 6
Vierte Ableitung: f (4)(x) = 0
Fünfte Ableitung: f (5)(x) = 0 usw.
Was wir hier getan haben, ist, dass wir zuerst die Potenzregel auf f(x) angewendet haben, um seine erste Ableitung, f'(x), zu erhalten, dann die Potenzregel auf die erste Ableitung angewendet haben, um die zweite zu erhalten, und so weiter. Die Ableitung wird schließlich auf Null gehen, wenn die Differenzierung wiederholt angewendet wird.
Die Anwendung der Produkt- und Quotientenregeln bleibt auch gültig, um Ableitungen höherer Ordnung zu erhalten, aber ihre Berechnung kann mit zunehmender Ordnung immer unordentlicher werden. Die allgemeine Leibniz-Regel vereinfacht die Aufgabe in diesem Aspekt, indem sie die Produktregel auf verallgemeinert:
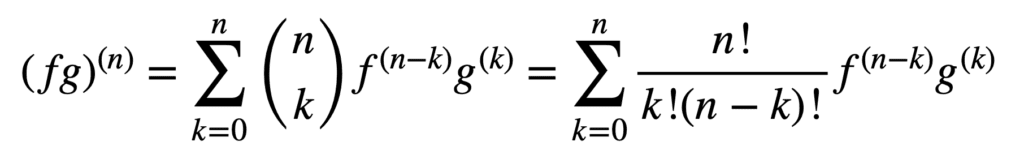
Hier der Begriff, n! / k!(n – k)!, ist der Binomialkoeffizient aus dem Binomialsatz, während f (k) und g(k) die k-te Ableitung der Funktionen f bzw.
Wenn wir also die erste und die zweite Ableitung finden (und daher n = 1 bzw. n = 2 ersetzen), erhalten wir nach der allgemeinen Leibniz-Regel:
(fg)(1) = (fg)‘ = f (1) g + f g(1)
( fg)(2) = (fg)“ = f (2) g + 2f (1) g(1) + f g(2)
Beachten Sie die bekannte erste Ableitung gemäß der Produktregel. Die Leibniz-Regel kann auch verwendet werden, um Ableitungen höherer Ordnung rationaler Funktionen zu finden, da der Quotient effektiv in ein Produkt der Form f g-1 ausgedrückt werden kann.
Ableitungen höherer Ordnung von multivariaten Funktionen
Die Definition von partiellen Ableitungen höherer Ordnung von multivariaten Funktionen ist analog zum univariaten Fall: die partielle Ableitung n-ter Ordnung für n > 1 wird als partielle Ableitung der (n – 1) -ten partiellen Ableitung berechnet. Zum Beispiel führt die zweite partielle Ableitung einer Funktion mit zwei Variablen zu vier zweiten partiellen Ableitungen: zwei eigene partielle Ableitungen, fxx und fyy, und zwei kreuzpartielle Ableitungen, fxy und fyx.
Um eine „Ableitung“ zu nehmen, müssen wir eine partielle Ableitung in Bezug auf x oder y nehmen, und es gibt vier Möglichkeiten, dies zu tun: x dann x, x dann y, y dann x, y dann y.
– Seite 371, Single and Multivariable Calculus, 2020.
Betrachten wir die multivariate Funktion f(x, y) = x2 + 3xy + 4y2, für die wir die zweiten partiellen Ableitungen finden möchten. Der Prozess beginnt mit dem Auffinden seiner partiellen Ableitungen erster Ordnung, zuerst: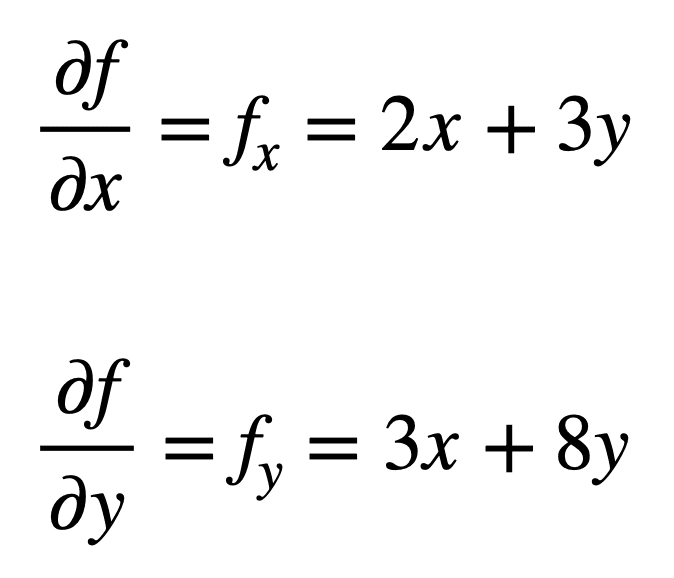
Die vier partiellen Ableitungen zweiter Ordnung werden dann gefunden, indem der Vorgang des Auffindens der partiellen Ableitungen der partiellen Ableitungen wiederholt wird. Die eigenen partiellen Ableitungen sind am einfachsten zu finden, da wir den partiellen Differenzierungsprozess in Bezug auf x oder y einfach ein zweites Mal wiederholen:
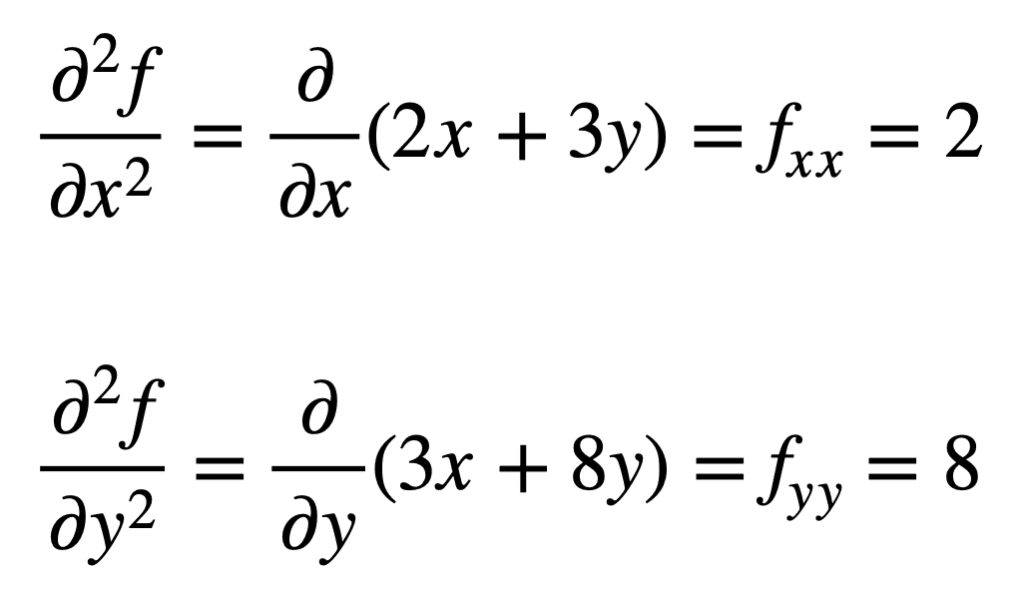
Die kreuzpartielle Ableitung des zuvor gefundenen fx (dh die partielle Ableitung in Bezug auf x) wird gefunden, indem die partielle Ableitung des Ergebnisses in Bezug auf y genommen wird, wodurch wir fxy erhalten. In ähnlicher Weise ergibt die partielle Ableitung von fy in Bezug auf x fyx:
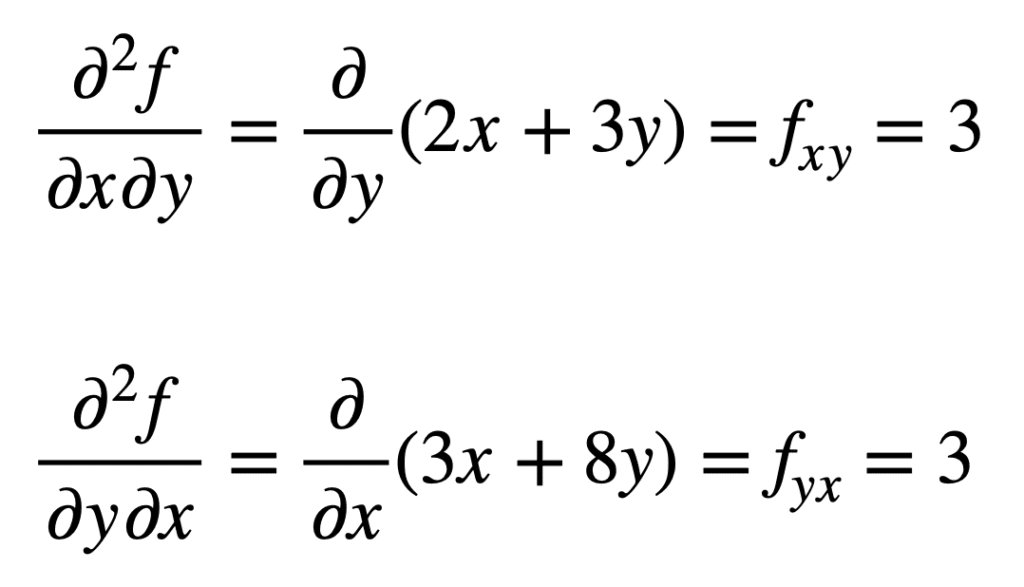
Es ist kein Zufall, dass die kreuzpartiellen Ableitungen das gleiche Ergebnis liefern. Dies wird durch den Satz von Clairaut definiert, der besagt, dass, solange die kreuzpartiellen Ableitungen stetig sind, sie gleich sind.
Anwendung im maschinellen Lernen
Im maschinellen Lernen wird meistens die Ableitung zweiter Ordnung verwendet. Wir hatten bereits erwähnt, dass die zweite Ableitung uns Informationen liefern kann, die die erste Ableitung allein nicht erfassen kann. Insbesondere kann es uns sagen, ob ein kritischer Punkt ein lokales Minimum oder Maximum ist (basierend darauf, ob die zweite Ableitung größer oder kleiner als Null ist), für die die erste Ableitung andernfalls in beiden Fällen Null wäre.
Es gibt mehrere Optimierungsalgorithmen zweiter Ordnung, die diese Informationen nutzen, von denen einer Newtons Methode ist.
Informationen zweiter Ordnung ermöglichen es uns dagegen, eine quadratische Approximation der Zielfunktion vorzunehmen und die richtige Schrittweite zu approximieren, um ein lokales Minimum zu erreichen …
– Seite 87, Algorithmen zur Optimierung, 2019.
Im univariaten Fall verwendet Newtons Methode eine Taylorreihenerweiterung zweiter Ordnung, um die quadratische Approximation um einen Punkt der Zielfunktion durchzuführen. Die Aktualisierungsregel für Newtons Methode, die durch Setzen der Ableitung auf Null und Lösen nach der Wurzel erhalten wird, beinhaltet eine Divisionsoperation durch die zweite Ableitung. Wenn Newtons Methode auf multivariate Optimierung erweitert wird, wird die Ableitung durch den Gradienten ersetzt, während der Kehrwert der zweiten Ableitung durch die Inverse der Hessischen Matrix ersetzt wird.
Wir werden die Approximationen der Hessischen und Taylor-Reihe, die die Verwendung von Derivaten höherer Ordnung nutzen, in separaten Tutorials behandeln.
Weiterführende Literatur
Dieser Abschnitt enthält weitere Ressourcen zu diesem Thema, wenn Sie tiefer gehen möchten.
Bücher
- Single and Multivariable Calculus, 2020.
- Kalkül für Dummies, 2016.
- Tiefes Lernen, 2017.
- Algorithmen zur Optimierung, 2019.
Zusammenfassung
In diesem Tutorial erfuhren Sie, wie Sie univariate und multivariate Ableitungen höherer Ordnung berechnen.
Insbesondere haben Sie gelernt:
- Wie man die Ableitungen höherer Ordnung von univariaten Funktionen berechnet.
- Wie man die Ableitungen höherer Ordnung von multivariaten Funktionen berechnet.
- Wie die Ableitungen zweiter Ordnung im maschinellen Lernen durch Optimierungsalgorithmen zweiter Ordnung ausgenutzt werden können.
