tento příklad je založen na statistice kriminality FBI z roku 2006. Zvláště nás zajímá vztah mezi velikostí státu a počtem vražd ve městě.
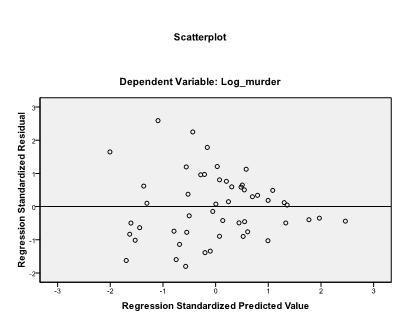
nejprve musíme zkontrolovat, zda v datech Existuje lineární vztah. Za tímto účelem zkontrolujeme scatterplot. Rozptylový graf ukazuje dobrý lineární vztah, který nám umožňuje provádět lineární regresní analýzu. Můžeme také zkontrolovat Pearsonovu Bivariátní korelaci a zjistit, že obě proměnné jsou vysoce korelované (r = .959 S p < 0,001).

Objevte, jak pomáháme upravovat kapitoly Disertační práce
zarovnání teoretického rámce, shromažďování článků, syntéza mezer, formulování jasné metodiky a datového plánu a psaní o teoretických a praktických důsledcích vašeho výzkumu jsou součástí našich komplexních služeb pro editaci disertační práce.
- Přineste odbornost editace disertační práce do kapitol 1-5 včas.
- Sledujte všechny změny a poté s vámi spolupracujte na vědeckém psaní.
- pokračující podpora při řešení zpětné vazby výboru, snížení revizí.
za druhé musíme zkontrolovat vícerozměrnou normálnost. V našem příkladu zjistíme, že vícerozměrná normalita nemusí být přítomna.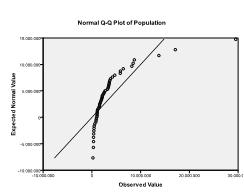
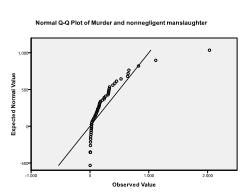
kolmogorovův-Smirnovův test toto podezření potvrzuje (p = 0,002 a p = 0.006). Provedení transformace ln na obou proměnných řeší problém a stanoví vícerozměrnou normálnost (K-S test p = .991 a p = .543).
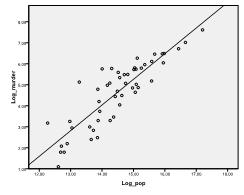
nyní můžeme provést lineární regresní analýzu. Lineární regrese se nachází v SPSS v analýze / regresi / Lineární…
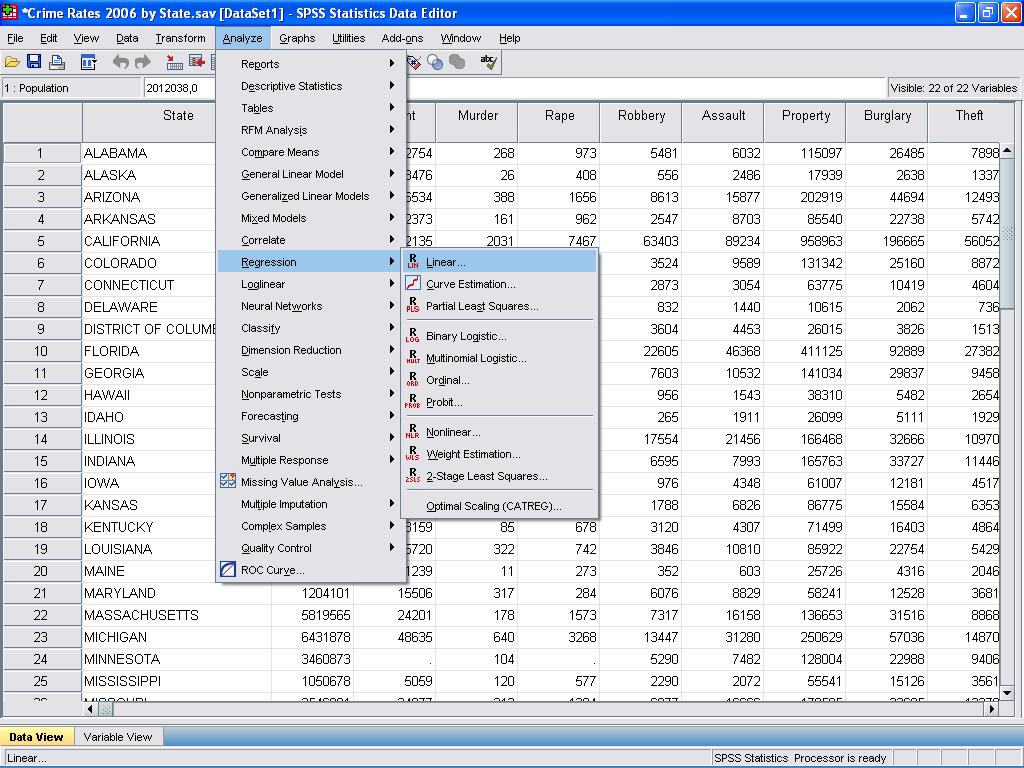
v tomto jednoduchém případě stačí do modelu přidat proměnné log_pop a log_murder jako závislé a nezávislé proměnné.
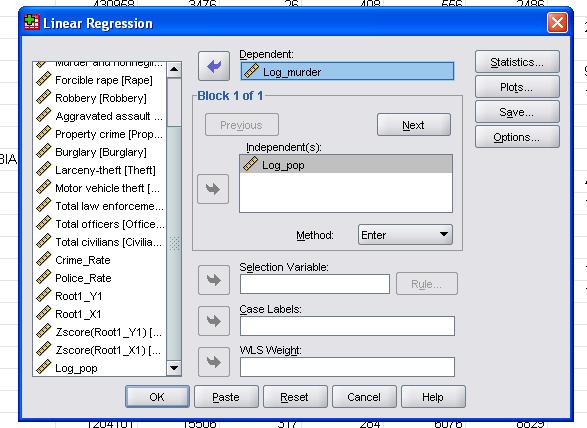
polní statistika nám umožňuje zahrnout další statistiky, které potřebujeme k posouzení platnosti naší lineární regresní analýzy.
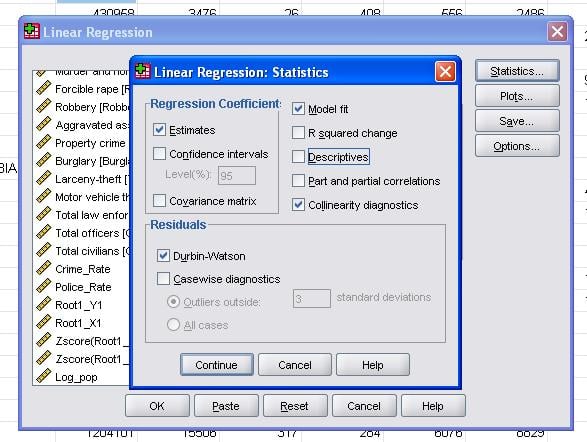
je vhodné dodatečně zahrnout diagnostiku kolinearity a Durbin-Watsonův test pro automatickou korelaci. Abychom otestovali předpoklad homoscedasticity zbytků, zahrnujeme do nabídky Parcel také speciální graf.
syntaxe SPSS pro lineární regresní analýzu je
regrese
/ chybí LISTWISE
/ STATISTICS COEFF OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) POUT(.10)
/ NOORIGIN
/ DEPENDENT Log_murder
/ METHOD=ENTER Log_pop
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS DURBIN HIST (ZRESID).
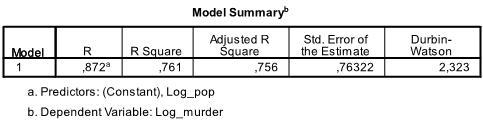
první tabulka výstupu zobrazuje souhrn modelu a celkovou statistiku fit. Zjistili jsme, že upravený R2 našeho modelu je 0,756 s R2 =.761 to znamená, že lineární regrese vysvětluje 76.1% rozptylu v datech. Durbin-Watson d = 2,323, což je mezi dvěma kritickými hodnotami 1,5 < d < 2,5, a proto můžeme předpokládat, že v datech neexistuje lineární automatická korelace prvního řádu.
následující tabulka je F-test, F-test lineární regrese má nulovou hypotézu, že mezi oběma proměnnými neexistuje lineární vztah (jinými slovy R2=0). S F = 156.2 a 50 stupňů volnosti test je velmi významný, takže můžeme předpokládat, že mezi proměnnými v našem modelu existuje lineární vztah.

následující tabulka ukazuje regresní koeficienty, intercept a význam všech koeficientů a intercept v modelu. Zjistili jsme, že naše lineární regresní analýza odhaduje lineární regresní funkci na y = -13.067 + 1.222
* x. Vezměte prosím na vědomí, že se to nepřekládá tam je 1.2 další vraždy za každých 1000 dalších obyvatel, protože jsme Ln transformovali proměnné.
kdybychom znovu spustili lineární regresní analýzu s původními proměnnými, skončili bychom s y = 11.85 + 6.7*10-5 což ukazuje, že na každých 10 000 dalších obyvatel bychom očekávali 6,7 dalších vražd.
v naší lineární regresní analýze test testuje nulovou hypotézu, že koeficient je 0. T-test zjistil, že intercept i proměnná jsou velmi významné (p < 0,001), a tak bychom mohli říci, že se liší od nuly.

tato tabulka také zahrnuje váhy Beta (které vyjadřují relativní význam nezávislých proměnných)a statistiky kolinearity. Protože však v naší analýze máme pouze 1 nezávislou proměnnou, nevěnujeme těmto hodnotám pozornost.
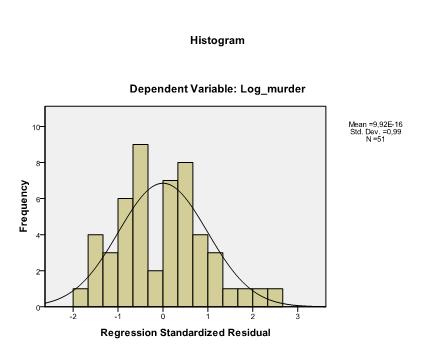
poslední věc, kterou musíme zkontrolovat, je homoscedasticita a normálnost zbytků. Histogram ukazuje, že zbytky se přibližují normálnímu rozdělení. Q-Q-graf z * pred a z * presid nám ukazuje, že v naší lineární regresní analýze neexistuje žádná tendence v chybových termínech.