Derivat med högre ordning

Senast uppdaterad den 31 juli 2021

derivat med högre ordning kan fånga information om en funktion som första ordningens derivat på egen hand inte kan fånga.

första ordningens derivat kan fånga viktig information, såsom förändringstakten, men på egen hand kan de inte skilja mellan lokala minima eller maxima, där förändringstakten är noll för båda. Flera optimeringsalgoritmer adresserar denna begränsning genom att utnyttja användningen av högre ordningsderivat, till exempel i Newtons metod där andra ordningens derivat används för att nå det lokala minimumet för en optimeringsfunktion.

i denna handledning kommer du att upptäcka hur man beräknar univariata och multivariata derivat med högre ordning.

när du har slutfört denna handledning kommer du att veta:

• hur man beräknar de högre ordningens derivat av univariata funktioner.
• hur man beräknar de högre ordningens derivat av multivariata funktioner.
• hur andra ordningens derivat kan utnyttjas i maskininlärning med andra ordningens optimeringsalgoritmer.

Låt oss komma igång.

handledning Översikt

denna handledning är uppdelad i tre delar; de är:

• högre Ordningsderivat av univariata funktioner
• högre Ordningsderivat av multivariata funktioner
• tillämpning i maskininlärning

högre Ordningsderivat av univariata funktioner

förutom första ordningens derivat, som vi har sett kan ge oss viktig information om en funktion, såsom dess momentana förändringshastighet, kan derivat av högre ordning också vara lika användbara. Till exempel kan det andra derivatet mäta accelerationen för ett rörligt objekt, eller det kan hjälpa en optimeringsalgoritm att skilja mellan ett lokalt maximum och ett lokalt minimum.

att beräkna högre ordningens (andra, tredje eller högre) derivat av univariata funktioner är inte så svårt.

det andra derivatet av en funktion är bara derivatet av dess första derivat. Det tredje derivatet är derivatet av det andra derivatet, det fjärde derivatet är derivatet av det tredje och så vidare.

därför innebär beräkning av högre ordningsderivat helt enkelt att differentiera funktionen upprepade gånger. För att göra det kan vi helt enkelt tillämpa vår kunskap om maktregeln. Låt oss betrakta funktionen, f(x) = x3 + 2×2 – 4x + 1, som ett exempel. Sedan:

första derivat: f'(x) = 3×2 + 4x-4

andra derivat: f ”(x) = 6x + 4

tredje derivat: f ”’ (x) = 6

fjärde derivat: f (4) (x) = 0

femte derivat: f( 5) (x) = 0 etc.

vad vi har gjort här är att vi först har tillämpat kraftregeln på f (x) för att få sitt första derivat, f'(x), sedan tillämpat kraftregeln på det första derivatet för att få det andra, och så vidare. Derivatet kommer så småningom att gå till noll när differentiering tillämpas upprepade gånger.

tillämpningen av produkt-och kvotreglerna förblir också giltig för att erhålla derivat av högre ordning, men deras beräkning kan bli messier och messier när ordern ökar. Den allmänna Leibniz-regeln förenklar uppgiften i denna aspekt genom att generalisera produktregeln till:

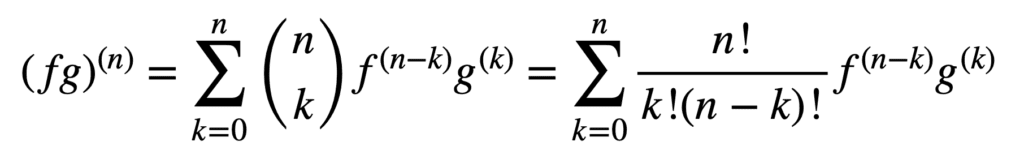
här termen, n! / k!(n – k)!, är binomialkoefficienten från Binomialsatsen, medan f(k) och g (k) betecknar KTH-derivatet av funktionerna, f respektive g.

därför ger vi de första och andra derivaten (och därmed ersätter n = 1 respektive n = 2) med den allmänna Leibniz-regeln:

(fg) (1) = (fg) ’ = f (1) g + f g(1)

(fg)(2) = (fg)” = f (2) g + 2F (1) g(1) + f g(2)

Lägg märke till det välbekanta första derivatet enligt definitionen i produktregeln. Leibniz-regeln kan också användas för att hitta högre ordningsderivat av rationella funktioner, eftersom kvoten effektivt kan uttryckas i en produkt av formen, f g-1.

högre Ordningsderivat av multivariata funktioner

definitionen av högre ordningens partiella derivat av multivariata funktioner är analog med det univariata fallet: n: te ordningens partiella derivat för n > 1, beräknas som det partiella derivatet av (n – 1)ordningens partiella derivat. Till exempel tar det andra partiella derivatet av en funktion med två variabler resulterar i fyra, andra partiella derivat: två egna partiella derivat, fxx och fyy, och två korspartiella derivat, fxy och fyx.

för att ta ett ”derivat” måste vi ta ett partiellt derivat med avseende på x eller y, och det finns fyra sätt att göra det: x sedan x, x sedan y, y sedan x, y sedan y.

– sida 371, singel och multivariabel kalkyl, 2020.

låt oss överväga den multivariata funktionen, f(x, y) = x2 + 3XY + 4y2, för vilken vi skulle vilja hitta de andra partiella derivaten. Processen börjar med att hitta sina första ordningens partiella derivat, först: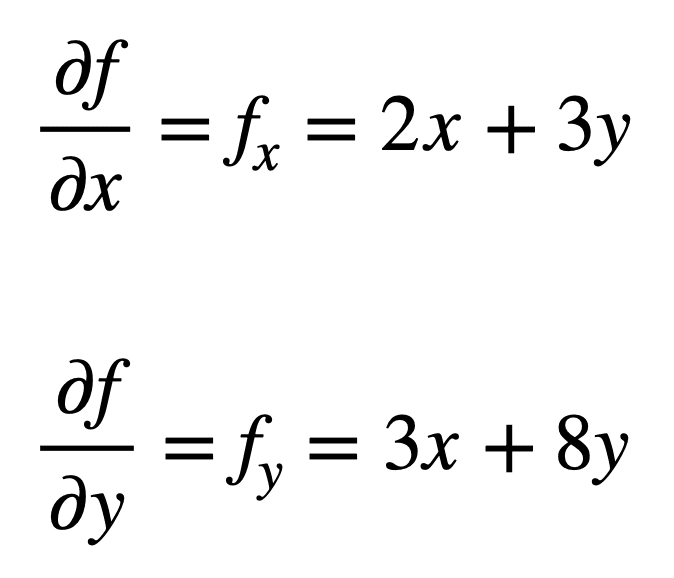

de fyra, andra ordningens partiella derivat hittas sedan genom att upprepa processen att hitta de partiella derivaten, av de partiella derivaten. De egna partiella derivaten är de enklaste att hitta, eftersom vi helt enkelt upprepar den partiella differentieringsprocessen, med avseende på antingen x eller y, en andra gång:

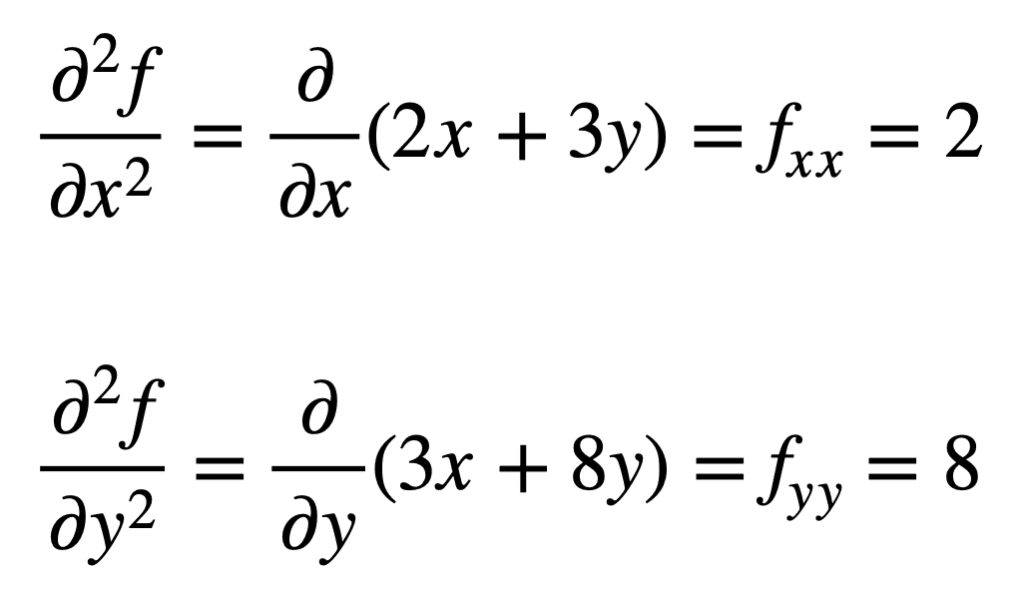
korspartiella derivatet av den tidigare hittade fx (det vill säga det partiella derivatet med avseende på x) hittas genom att ta det partiella derivatet av resultatet med avseende på y, vilket ger oss fxy. På samma sätt tar vi det partiella derivatet av fy med avseende på x, ger oss fyx:

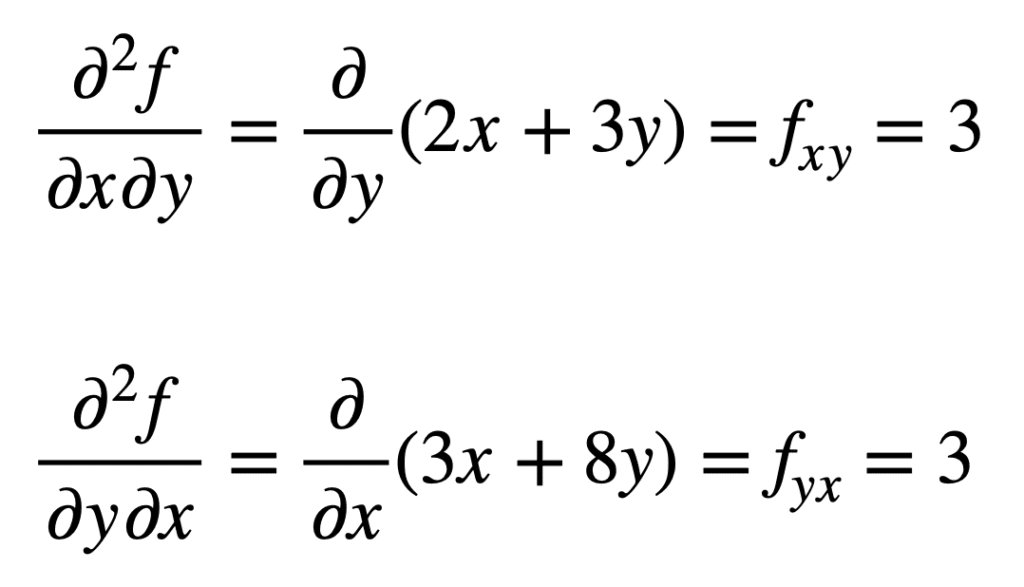
det är inte av misstag att korspartiella derivat ger samma resultat. Detta definieras av Clairauts teorem, som säger att så länge korspartiella derivat är kontinuerliga, så är de lika.

tillämpning i maskininlärning

i maskininlärning är det andra ordningens derivat som mest används. Vi hade tidigare nämnt att det andra derivatet kan ge oss information som det första derivatet på egen hand inte kan fånga. Specifikt kan det berätta om en kritisk punkt är ett lokalt minimum eller maximalt (baserat på om det andra derivatet är större eller mindre än noll), för vilket det första derivatet annars skulle vara noll i båda fallen.

det finns flera andra ordningens optimeringsalgoritmer som utnyttjar denna information, varav en är Newtons metod.

andra ordningens information, å andra sidan, tillåter oss att göra en kvadratisk approximation av objektivfunktionen och approximera rätt stegstorlek för att nå ett lokalt minimum …

– sidan 87, algoritmer för optimering, 2019.

i det univariata fallet använder Newtons metod en andra ordningens Taylor-serieutvidgning för att utföra den kvadratiska approximationen runt någon punkt på objektivfunktionen. Uppdateringsregeln för Newtons metod, som erhålls genom att ställa derivatet till noll och lösa för roten, innefattar en delningsoperation av det andra derivatet. Om Newtons metod utvidgas till multivariat optimering ersätts derivatet med gradienten, medan det ömsesidiga av det andra derivatet ersätts med det inversa av den hessiska matrisen.

vi ska täcka Hessian och Taylor-serien approximationer, som utnyttjar användningen av högre ordningsderivat, i separata handledning.

Vidare läsning

det här avsnittet ger mer resurser om ämnet om du vill gå djupare.

böcker

• enkel och multivariabel kalkyl, 2020.
• Kalkyl för Dummies, 2016.
• Djupt Lärande, 2017.
• algoritmer för optimering, 2019.

sammanfattning

i denna handledning upptäckte du hur man beräknar högre ordningens univariata och multivariata derivat.

specifikt lärde du dig:

• hur man beräknar de högre ordningens derivat av univariata funktioner.
• hur man beräknar de högre ordningens derivat av multivariata funktioner.
• hur andra ordningens derivat kan utnyttjas i maskininlärning med andra ordningens optimeringsalgoritmer.