detta exempel är baserat på FBI: s brottsstatistik 2006. Vi är särskilt intresserade av förhållandet mellan statens storlek och antalet mord i staden.
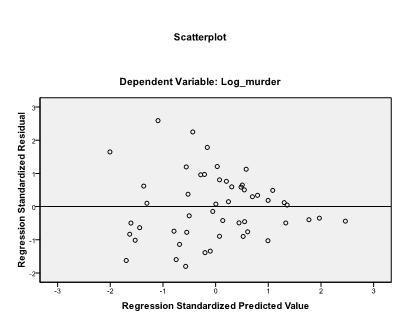
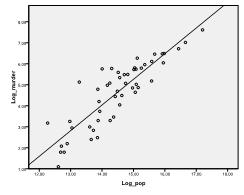
först måste vi kontrollera om det finns ett linjärt förhållande i data. För det kontrollerar vi scatterplot. Scatter-diagrammet indikerar ett bra linjärt förhållande, vilket gör det möjligt för oss att genomföra en linjär regressionsanalys. Vi kan också kontrollera Pearsons bivariata korrelation och finna att båda variablerna är starkt korrelerade (r = .959 med p < 0,001).

Upptäck hur vi hjälper till att redigera dina Avhandlingskapitel
anpassa teoretiska ramar, samla artiklar, syntetisera luckor, formulera en tydlig metodik och dataplan och skriva om de teoretiska och praktiska konsekvenserna av din forskning är en del av våra omfattande avhandlingstjänster.
- ta med avhandlingsredigeringsexpertis till kapitel 1-5 i tid.
- spåra alla ändringar och arbeta sedan med dig för att få till stånd vetenskapligt skrivande.
- pågående stöd för att ta itu med utskottets feedback, minska revideringar.
för det andra måste vi kontrollera om multivariat normalitet. I vårt exempel finner vi att multivariat normalitet kanske inte är närvarande.
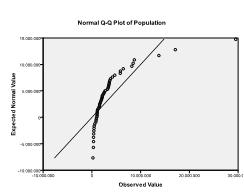
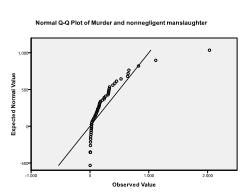
Kolmogorov-Smirnov-testet bekräftar denna misstanke (p = 0, 002 och p = 0.006). Att genomföra en ln-transformation på de två variablerna åtgärdar problemet och etablerar multivariat normalitet (ks-test p = .991 och p = .543).
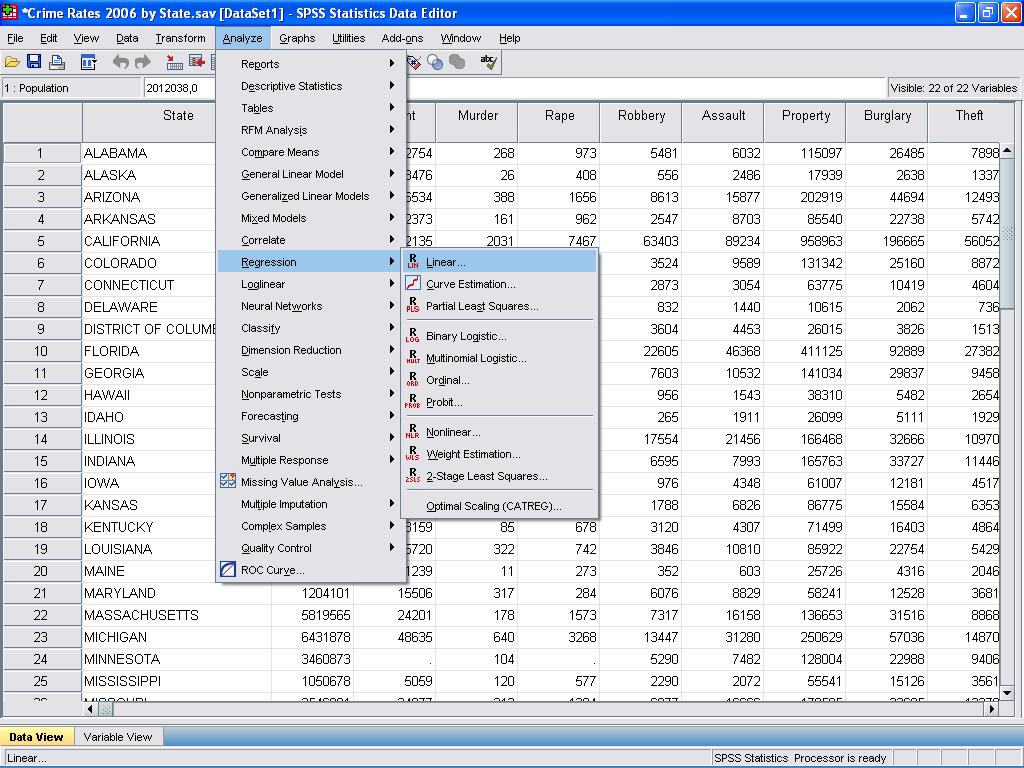
vi kan nu genomföra den linjära regressionsanalysen. Linjär regression finns i SPSS i Analysera / Regression / linjär…
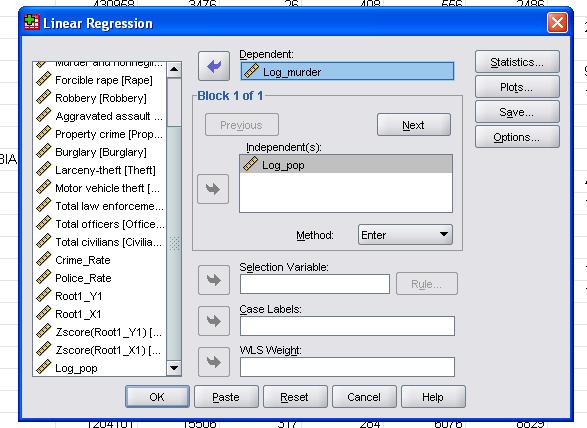
i det här enkla fallet behöver vi bara lägga till variablerna log_pop och log_murder till modellen som beroende och oberoende variabler.
fältstatistiken tillåter oss att inkludera ytterligare statistik som vi behöver för att bedöma giltigheten av vår linjära regressionsanalys.
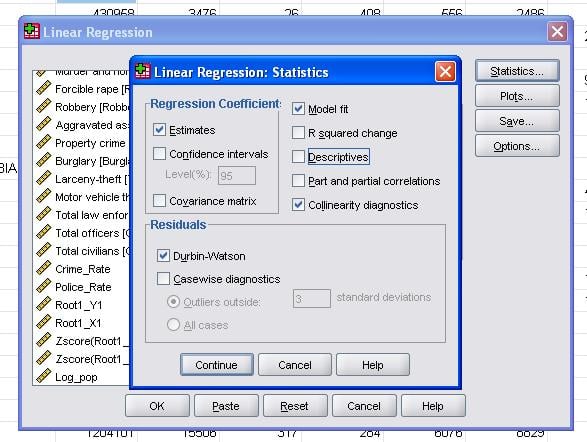
det är tillrådligt att dessutom inkludera kollinearitetsdiagnostik och Durbin-Watson-testet för automatisk korrelation. För att testa antagandet om homoscedasticitet av rester inkluderar vi också en speciell tomt i menyn tomter.
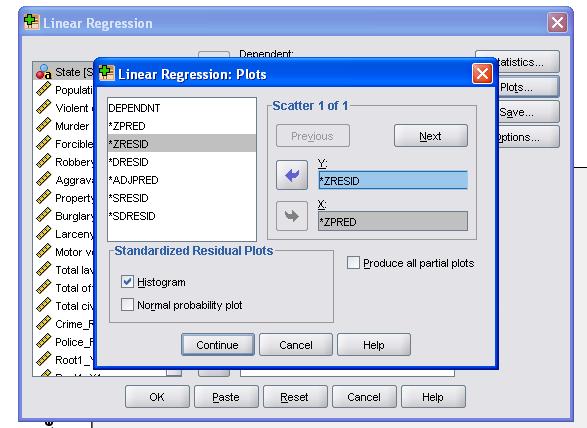
SPSS-syntaxen för den linjära regressionsanalysen är
REGRESSION
/saknas LISTVIS
/statistik COEFF OUTS R ANOVA COLLIN TOL
/kriterier=PIN(.05) vitlinglyra(.10)
/ NOORIGIN
/beroende Log_murder
/metod=ange Log_pop
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/ rester DURBIN HIST(ZRESID).
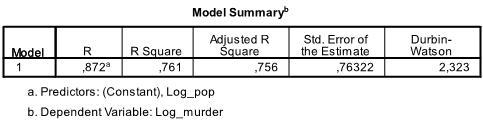
utmatningens första tabell visar modellöversikt och övergripande passningsstatistik. Vi finner att den justerade R2 i vår modell är 0,756 med R2 = .761 det betyder att den linjära regressionen förklarar 76.1% av variansen i data. Durbin-Watson d = 2.323, som ligger mellan de två kritiska värdena på 1.5 < d < 2.5 och därför kan vi anta att det inte finns någon första ordningens linjära auto-korrelation i data.
nästa tabell är F-testet, den linjära regressionens F-test har nollhypotesen att det inte finns något linjärt förhållande mellan de två variablerna (med andra ord R2=0). Med F = 156.2 och 50 frihetsgrader testet är mycket signifikant, så vi kan anta att det finns ett linjärt förhållande mellan variablerna i vår modell.


nästa tabell visar regressionskoefficienterna, avlyssningen och betydelsen av alla koefficienter och avlyssningen i modellen. Vi finner att vår linjära regressionsanalys uppskattar den linjära regressionsfunktionen att vara y = -13.067 + 1.222
* X. Observera att detta inte översätts i det finns 1.2 ytterligare mord för varje 1000 ytterligare invånare eftersom vi ln omvandlas variablerna.
om vi körde den linjära regressionsanalysen med de ursprungliga variablerna skulle vi sluta med y = 11.85 + 6.7*10-5 vilket visar att för varje 10 000 ytterligare invånare skulle vi förvänta oss att se 6,7 ytterligare mord.
i vår linjära regressionsanalys testar testet nollhypotesen att koefficienten är 0. T-testet finner att både intercept och variabel är mycket signifikanta (p < 0.001) och därmed kan vi säga att de skiljer sig från noll.

denna tabell innehåller också Betavikterna (som uttrycker den relativa betydelsen av oberoende variabler) och kollinearitetsstatistiken. Men eftersom vi bara har 1 oberoende variabel i vår analys uppmärksammar vi inte dessa värden.
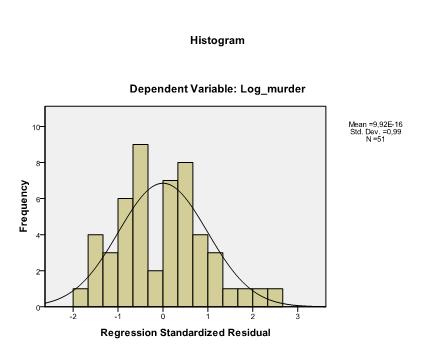
det sista vi behöver kontrollera är homoscedasticiteten och normaliteten hos rester. Histogrammet indikerar att resterna approximerar en normalfördelning. Q-Q-Plot av z * pred och z*predid visar oss att i vår linjära regressionsanalys finns det ingen tendens i feltermerna.