Derivatele de ordin superior

Ultima actualizare la 31 iulie 2021

derivatele de ordin superior pot capta informații despre o funcție pe care derivatele de ordinul întâi nu o pot capta singure.

derivatele de ordinul întâi pot capta informații importante, cum ar fi rata de schimbare, dar pe cont propriu nu pot distinge între minimele sau maximele locale, unde rata de schimbare este zero pentru ambele. Mai mulți algoritmi de optimizare abordează această limitare exploatând utilizarea derivatelor de ordin superior, cum ar fi în metoda lui Newton unde derivatele de ordinul doi sunt utilizate pentru a atinge minimul local al unei funcții de optimizare.

în acest tutorial, veți descoperi cum să calculați derivatele univariate și multivariate de ordin superior.

după finalizarea acestui tutorial, veți ști:

• cum se calculează derivatele de ordin superior ale funcțiilor univariate.
• cum se calculează derivatele de ordin superior ale funcțiilor multivariate.
• modul în care derivatele de ordinul doi pot fi exploatate în învățarea automată prin algoritmi de optimizare de ordinul doi.

să începem.

tutorial prezentare generală

acest tutorial este împărțit în trei părți; acestea sunt:

• derivate de ordin superior ale funcțiilor Univariate
• derivate de ordin superior ale funcțiilor Multivariate
• aplicație în învățarea automată

derivate de ordin superior ale funcțiilor Univariate

pe lângă derivatele de ordinul întâi, pe care le-am văzut ne pot oferi informații importante despre o funcție, cum ar fi rata instantanee de schimbare, derivatele de ordin superior pot fi, de asemenea, la fel de utile. De exemplu, al doilea derivat poate măsura accelerația unui obiect în mișcare sau poate ajuta un algoritm de optimizare să facă distincția între un maxim local și un minim local.

calculul derivatelor de ordin superior (al doilea, al treilea sau mai mare) ale funcțiilor univariate nu este atât de dificil.

a doua derivată a unei funcții este doar derivata primei sale derivate. Al treilea derivat este derivatul celui de-al doilea derivat, al patrulea derivat este derivatul celui de-al treilea și așa mai departe.

– pagina 147, calcul pentru manechine, 2016.

prin urmare, calculul derivatelor de ordin superior implică pur și simplu diferențierea funcției în mod repetat. Pentru a face acest lucru, putem pur și simplu să aplicăm cunoștințele noastre despre regula puterii. Să luăm în considerare funcția, f(x) = x3 + 2×2 – 4x + 1, ca exemplu. Apoi:

prima derivată: f'(x) = 3×2 + 4x – 4

a doua derivată: f”(x) = 6X + 4

a treia derivată: f”‘(x) = 6

a patra derivată: f (4)(x) = 0

a cincea derivată: f (5)(x) = 0 etc.

ceea ce am făcut aici este că am aplicat mai întâi Regula puterii la f(x) pentru a obține prima sa derivată, f'(x), apoi am aplicat regula puterii la prima derivată pentru a obține a doua și așa mai departe. Derivatul va merge, în cele din urmă, la zero, deoarece diferențierea este aplicată în mod repetat.

aplicarea produsului și a regulilor coeficientului rămâne valabilă și în obținerea derivatelor de ordin superior, dar calculul lor poate deveni mai dezordonat și mai dezordonat pe măsură ce ordinea crește. Regula generală Leibniz simplifică sarcina în acest aspect, generalizând regula produsului la:

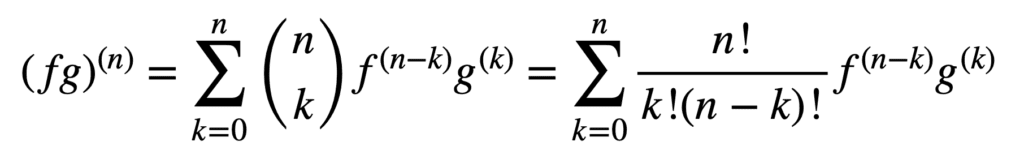
aici, termenul, n! / k!(n – k)!, este coeficientul binomial din teorema binomială, în timp ce f (k) și g(k) denotă derivata k a funcțiilor, respectiv f și G.

prin urmare, găsirea primului și a celui de-al doilea derivat (și, prin urmare, înlocuirea lui n = 1 și respectiv n = 2), prin regula generală Leibniz, ne dă:

(fg) (1) = (fg)’ = f (1) g + FG(1)

(fg) (2) = (fg)” = f (2) g + 2f(1) g(1) + f g (2)

observați prima derivată familiară definită de regula produsului. Regula Leibniz poate fi, de asemenea, utilizată pentru a găsi derivate de ordin superior ale funcțiilor raționale, deoarece coeficientul poate fi exprimat efectiv într-un produs al formei, f g-1.

derivate de ordin superior ale funcțiilor Multivariate

definiția derivatelor parțiale de ordin superior ale funcțiilor multivariate este analogă cazului univariate: derivata parțială de ordinul n Pentru n > 1, este calculată ca derivata parțială a derivatei parțiale de ordinul n – 1. De exemplu, luând a doua derivată parțială a unei funcții cu două variabile rezultă patru, a doua derivată parțială: două derivate parțiale proprii, fxx și fyy și două derivate parțiale încrucișate, fxy și fyx.

Pentru a lua o „derivată”, trebuie să luăm o derivată parțială în raport cu x sau y și există patru moduri de a o face: x apoi x, x apoi y, y apoi x, y apoi y.

– pagina 371, calcul unic și multivariabil, 2020.

să luăm în considerare funcția multivariată, f(x, y) = x2 + 3XY + 4y2, pentru care am dori să găsim a doua derivată parțială. Procesul începe cu găsirea derivatelor sale parțiale de ordinul întâi, mai întâi: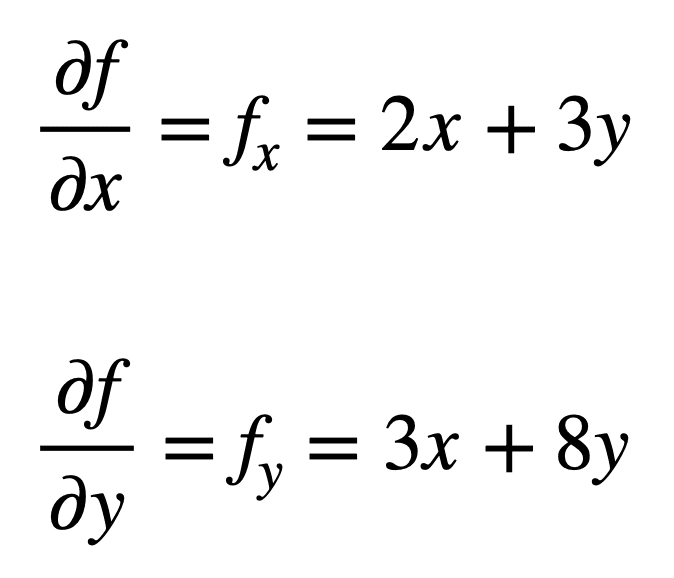

cele patru derivate parțiale de ordinul doi sunt apoi găsite prin repetarea procesului de găsire a derivatelor parțiale, a derivatelor parțiale. Derivatele parțiale proprii sunt cele mai simple de găsit, deoarece repetăm pur și simplu procesul de diferențiere parțială, cu privire la x sau y, a doua oară:

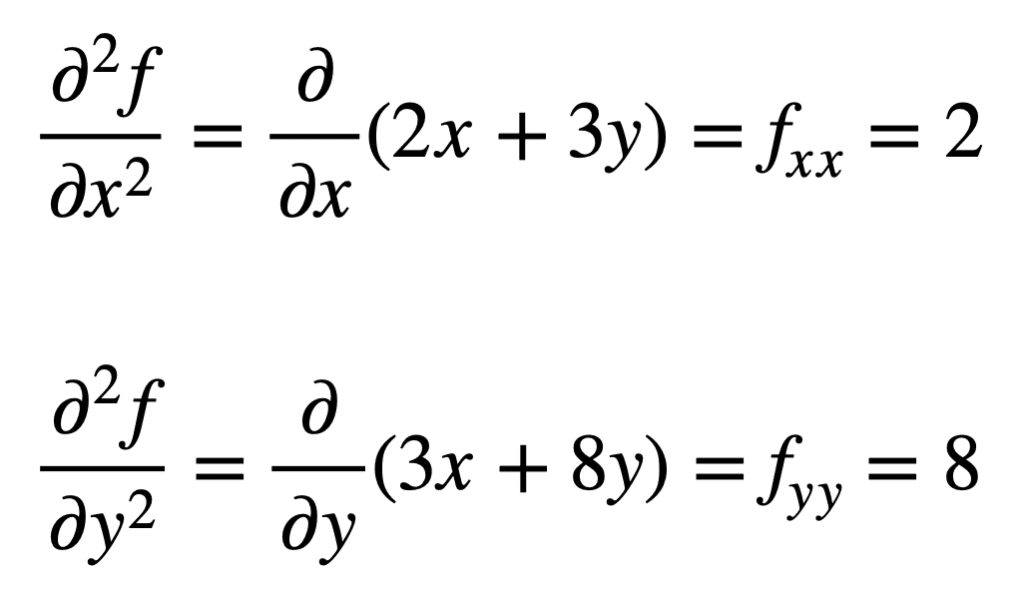
derivata parțială încrucișată a fx găsită anterior (adică derivata parțială în raport cu x) se găsește luând derivata parțială a rezultatului în raport cu y, oferindu-ne fxy. În mod similar, luând derivata parțială a fy în raport cu x, ne dă fyx:

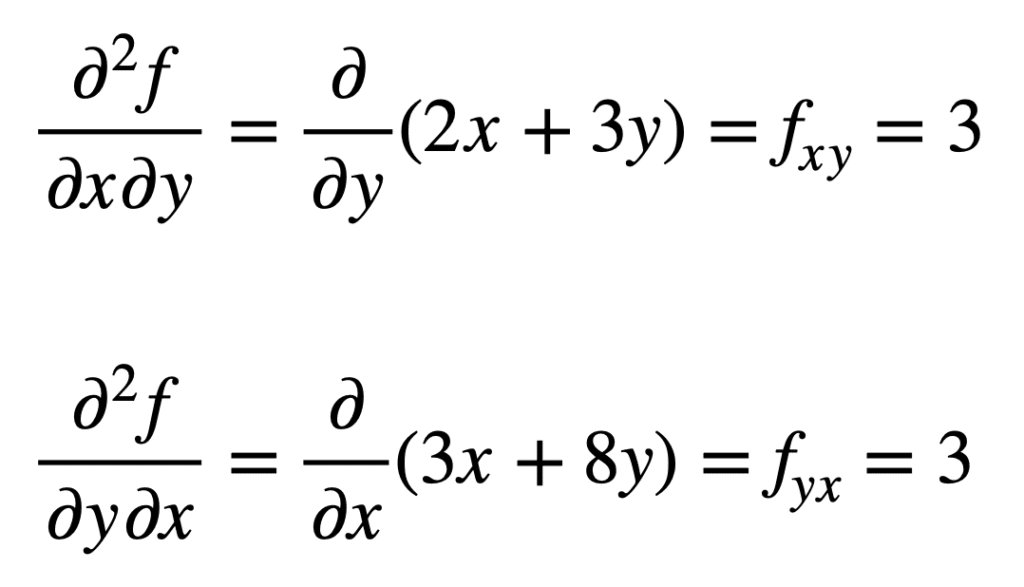
nu este întâmplător faptul că derivatele parțiale încrucișate dau același rezultat. Acest lucru este definit de teorema lui Clairaut, care afirmă că atâta timp cât derivatele parțiale încrucișate sunt continue, atunci sunt egale.

aplicație în învățarea automată

în învățarea automată, este derivata de ordinul doi care este utilizată în cea mai mare parte. Am menționat anterior că a doua derivată ne poate furniza informații pe care prima derivată singură nu le poate capta. Mai exact, ne poate spune dacă un punct critic este un minim sau maxim local (pe baza faptului că al doilea derivat este mai mare sau mai mic decât zero, respectiv), pentru care primul derivat ar fi, altfel, zero în ambele cazuri.

există mai mulți algoritmi de optimizare de ordinul doi care folosesc aceste informații, dintre care unul este metoda lui Newton.

informațiile de ordinul doi, pe de altă parte, ne permit să facem o aproximare pătratică a funcției obiective și să aproximăm dimensiunea corectă a pasului pentru a atinge un minim local …

-pagina 87, algoritmi pentru optimizare, 2019.

în cazul univariat, metoda lui Newton folosește o expansiune a seriei Taylor de ordinul doi pentru a efectua aproximarea pătratică în jurul unui punct al funcției obiective. Regula de actualizare pentru metoda lui Newton, care se obține prin setarea derivatului la zero și rezolvarea pentru rădăcină, implică o operație de divizare cu a doua derivată. Dacă metoda lui Newton este extinsă la optimizarea multivariată, derivata este înlocuită cu gradientul, în timp ce reciproca celei de-a doua derivate este înlocuită cu inversul matricei Hessiene.

vom acoperi aproximările seriilor Hessian și Taylor, care folosesc utilizarea derivatelor de ordin superior, în tutoriale separate.

lecturi suplimentare

această secțiune oferă mai multe resurse pe această temă dacă doriți să aprofundați.

Cărți

• calcul unic și multivariabil, 2020.
• calcul pentru manechine, 2016.
• Învățare Profundă, 2017.
• algoritmi pentru optimizare, 2019.

rezumat

în acest tutorial, ați descoperit cum să calculați derivatele univariate și multivariate de ordin superior.

mai exact, ai învățat:

• cum se calculează derivatele de ordin superior ale funcțiilor univariate.
• cum se calculează derivatele de ordin superior ale funcțiilor multivariate.
• modul în care derivatele de ordinul doi pot fi exploatate în învățarea automată prin algoritmi de optimizare de ordinul doi.