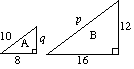o extindere este o transformare în care un obiect mapează la o imagine de aceeași formă, dar de dimensiuni diferite. Se spune că obiectul și imaginea sunt similare. O extindere necesită un centru de extindere și un factor de scară.
notație
E este o mărire, cu Centrul de mărire O și factorul de scală XV.
E: AB 
AB
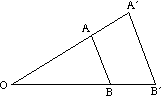
Proprietăți de extindere
triunghi PQR hărți la triunghi PQR sub extindere cu Centrul O.
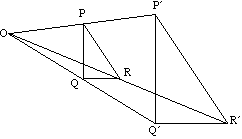
liniile și imaginile lor sunt întotdeauna paralele.
de exemplu, PQ este paralel cu PQ
dimensiunea unghiului este invariantă.
de exemplu
PQR =
Centrul extinderii este singurul punct invariant.
lungimea și aria nu sunt invariante, cu excepția cazului în care m = 1 sau − 1.
adică extinderea nu este o izometrie.
extinderea este o transformare directă.
adică
PQR și
în cazul în care factorul de scară pentru lungime este XC, m xc2 este factorul de scară pentru suprafață.
diferiți factori de scară
diagrama de mai jos arată efectul unei varietăți de factori de scară asupra măririi unui triunghi ABC despre centrul O.
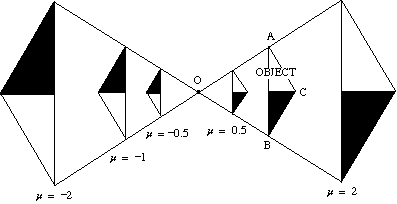
- dacă factorul de scară este pozitiv, atât obiectul, cât și imaginea se află pe aceeași parte a Centrului.
- dacă factorul de scară este negativ, obiectul și imaginea se află pe laturile opuse ale centrului.
imaginea este inversată.
a se vedea exemple de extinderi− 
localizarea centrului de extindere
având în vedere o figură și imaginea acesteia, pentru a găsi centrul de extindere:
1. Alăturați-vă un punct și imaginea sa.
2. Repetați pentru un alt punct și imaginea acestuia.
3. Centrul extinderii este intersecția acestor linii.
cifre similare
Cifrele sunt similare dacă au aceeași formă.
- figuri similare pot fi mapate una pe cealaltă printr-o mărire sau printr-o combinație de reflecție, rotație sau traducere și o mărire.
- unghiurile corespunzătoare ale figurilor similare sunt egale.
- laturile corespunzătoare sunt proporționale între ele.
tip 1
YXZ este similar cu PQM deoarece au unghiuri corespunzătoare egale.
|
|
 |
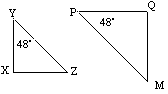YXZ poate fi mapat la PQM printr-o combinație de transformări.
factor de scară = = 
tip 2
ABC este similar cu ADE deoarece:
|
(DE este paralel cu BC) |
 |
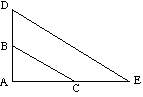ABC poate fi mapat pe ADE printr-o extindere.
factor de scară = = 
|
(a) (i) cele două triunghiuri A și B sunt similare. Găsiți p și Q. |
(a) (i) pentru a p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) aria triunghiului a este de 24 de unități2. |
(ii) factor de scală pentru aria = inqut2 = 4 aria triunghiului B= 4 x aria triunghiului a |
|
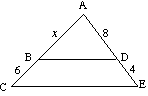
(B) Găsiți x, dacă BD este paralel cu CE |
(b) Pentru
  12x = 8 (x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B , factorul de scară = 2 
ABD
descărcați o foaie de calcul interactivă (Microsoft Excel) care prezintă reflecții, rotații, traduceri și extinderi.
(utilizatorii Windows, faceți clic dreapta și ” salvați ținta ca…”pentru a salva fișierele de pe computer.)
