Derivativos de ordem superior

última atualização em 31 de julho de 2021

derivativos de ordem superior podem capturar informações sobre uma função que derivativos de primeira ordem por conta própria não podem capturar. Derivativos de Primeira Ordem podem capturar informações importantes, como a taxa de mudança, mas por conta própria eles não podem distinguir entre mínimos ou máximos locais, onde a taxa de mudança é zero para ambos. Vários algoritmos de otimização abordam essa limitação explorando o uso de derivadas de ordem superior, como no método de Newton, onde as derivadas de segunda ordem são usadas para atingir o mínimo local de uma função de otimização.

neste tutorial, você descobrirá como calcular derivadas univariadas e multivariadas de ordem superior.

depois de concluir este tutorial, você saberá:

• como calcular as derivadas de ordem superior das funções univariadas.
• como calcular as derivadas de ordem superior de funções multivariadas.
• como as derivadas de segunda ordem podem ser exploradas no aprendizado de máquina por algoritmos de otimização de segunda ordem.

vamos começar.

Visão Geral do Tutorial

este tutorial é dividido em três partes; eles são:

• Maior-derivadas de Ordem de Univariada Funções
• Maior-derivadas de Ordem do Multivariada Funções
• Aplicação em Aprendizado de Máquina

Maior-derivadas de Ordem de Univariada Funções

além do primeiro-derivadas de ordem, o que temos visto nos podem fornecer importantes informações sobre uma função, tal como a sua taxa instantânea de variação, superior-derivadas de ordem também pode ser igualmente útil. Por exemplo, a segunda derivada pode medir a aceleração de um objeto em movimento ou pode ajudar um algoritmo de otimização a distinguir entre um máximo local e um mínimo local.

computar derivações de ordem superior (segunda, terceira ou superior) de funções univariadas não é tão difícil.

A segunda derivada de uma função é apenas a derivada de sua primeira derivada. A terceira derivada é a derivada da segunda derivada, a quarta derivada é a derivada da terceira e assim por diante.

– página 147, cálculo para Dummies, 2016.

portanto, computar derivadas de ordem superior simplesmente envolve diferenciar a função repetidamente. Para fazer isso, podemos simplesmente aplicar nosso conhecimento da Regra do poder. Vamos considerar a função, f ( x) = x3 + 2×2 – 4x + 1, como exemplo. Então:

Primeira derivada: f'(x) = 3×2 + 4x – 4

Segunda derivada: f”(x) = 6x + 4

Terceira derivada: f'(x) = 6

Quarta derivada: f (4)(x) = 0

Quinto derivada: f (5)(x) = 0, etc.O que fizemos aqui é que primeiro aplicamos a regra de potência A f (x) para obter sua primeira derivada, f'(x), depois aplicamos a regra de potência à primeira derivada para obter a segunda e assim por diante. A derivada, eventualmente, vai para zero à medida que a diferenciação é aplicada repetidamente.

A aplicação das regras do produto e do quociente também permanece válida na obtenção de derivativos de ordem superior, mas seu cálculo pode se tornar mais confuso e mais confuso à medida que a ordem aumenta. A regra geral Leibniz simplifica a tarefa neste aspecto, generalizando a Regra do produto para:

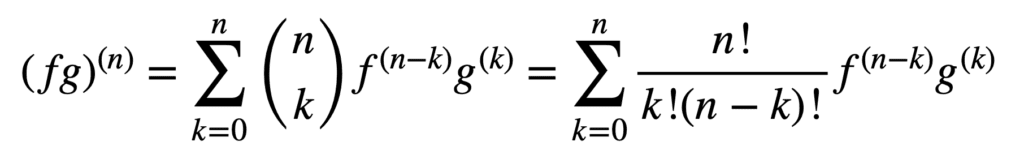
aqui, o termo, n! / k!(n-k)!, é o coeficiente binomial do teorema binomial, enquanto f (k) E g(k) denotam a KTH derivada das funções, f E g, respectivamente.

portanto, encontrar a primeira e a segunda derivadas (e, portanto, substituir n = 1 e n = 2, respectivamente), pela regra geral de Leibniz, nos dá:

(fg)(1) = (fg)’ = f (1) g + f g(1)

(fg)(2) = (fg)” = f (2) g + 2f (1) g(1) + f(2)

Observe que o familiar de primeiro de derivativos, conforme definido pela regra do produto. A regra de Leibniz também pode ser usada para encontrar derivadas de ordem superior de funções racionais, uma vez que o quociente pode ser efetivamente expresso em um produto da forma, f g-1.

derivadas de Ordem Superior de funções multivariadas

A definição de derivadas parciais de ordem superior de funções multivariadas é análoga ao caso univariado: a derivada parcial da enésima ordem para n > 1, é calculada como a derivada parcial da (n – 1)derivada parcial da enésima ordem. Por exemplo, tomar a segunda derivada parcial de uma função com duas variáveis resulta em quatro, segunda derivada parcial: duas derivadas parciais próprias, fxx e fyy, e duas derivadas parciais cruzadas, fxy e fyx.

Para dar um “derivado” temos de tomar uma derivada parcial com relação a x ou y, e há quatro maneiras de o fazer: x então x, x e depois y, y, então x, y, então y.

– Página 371, Único e Multivariável de Cálculo, 2020.

vamos considerar a função multivariada, f (x, y) = x2 + 3xy + 4y2, para a qual gostaríamos de encontrar as segundas derivadas parciais. O processo começa com a descoberta de seus derivados parciais de primeira ordem, primeiro: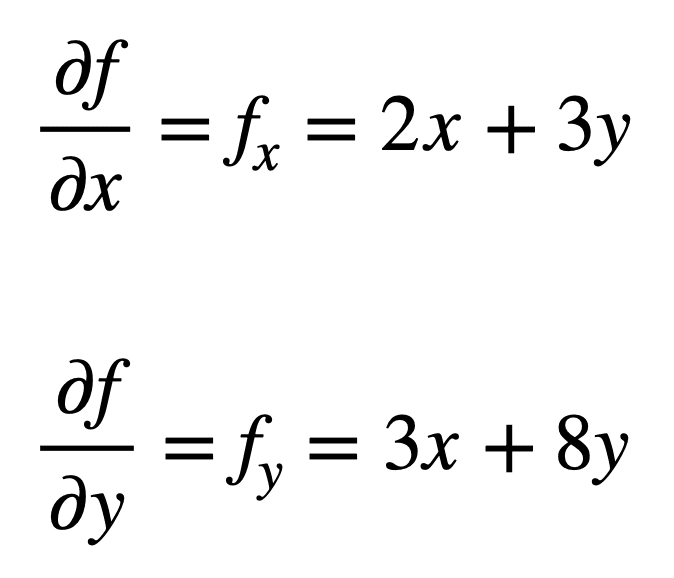

as quatro derivadas parciais de segunda ordem são então encontradas repetindo o processo de encontrar as derivadas parciais, das derivadas parciais. As próprias derivadas parciais são as mais simples de encontrar, uma vez que simplesmente repetimos o processo de diferenciação parcial, em relação a x ou y, uma segunda vez:

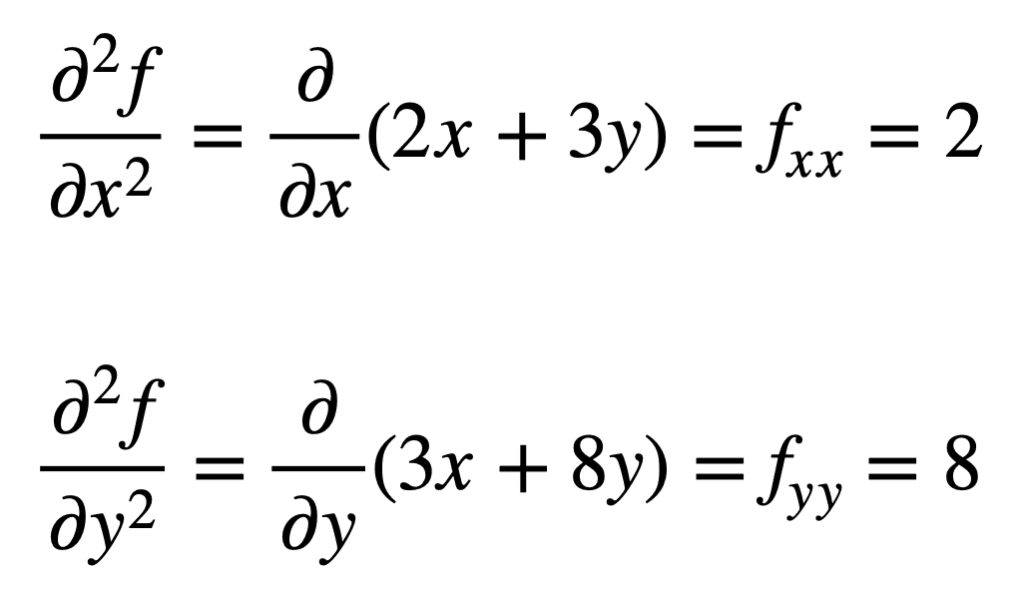
A cruz derivada parcial do encontrado anteriormente fx (isto é, a derivada parcial com relação a x) é encontrado tomando a derivada parcial do resultado com relação a y, dando-nos fxy. Da mesma forma, tomar a derivada parcial de fy em relação a x, nos dá fyx:

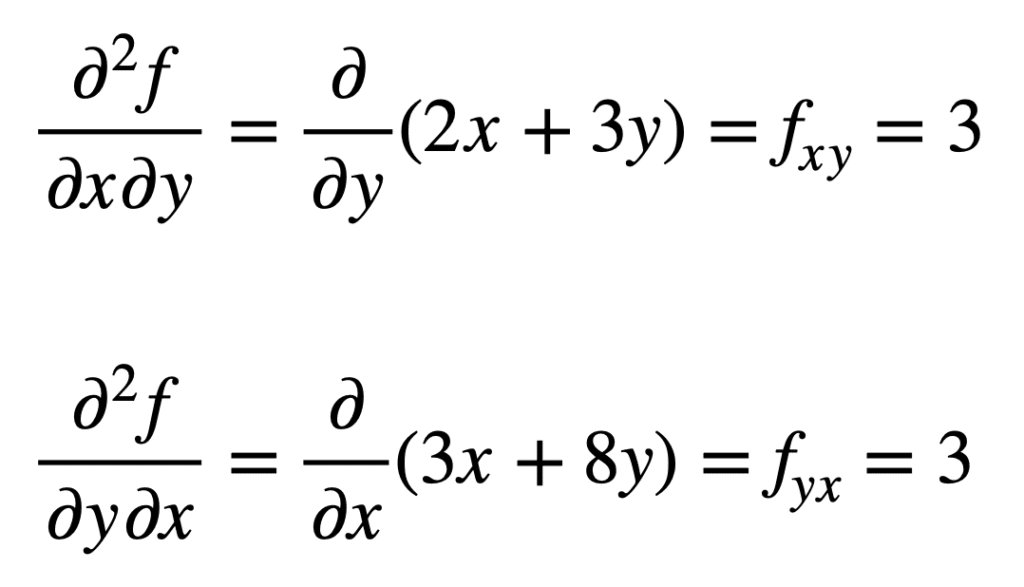
não é por acaso que os derivados parciais cruzados dão o mesmo resultado. Isso é definido pelo teorema de Clairaut, que afirma que, enquanto as derivadas parciais cruzadas forem contínuas, elas serão iguais.

aplicação em Aprendizado de máquina

em aprendizado de máquina, é a derivada de segunda ordem que é usada principalmente. Anteriormente, mencionamos que a segunda derivada pode nos fornecer informações que a primeira derivada por conta própria não pode capturar. Especificamente, ele pode nos dizer se um ponto crítico é um mínimo ou máximo local (com base em se a segunda derivada é maior ou menor que zero, respectivamente), para o qual a primeira derivada seria, caso contrário, zero em ambos os casos.

existem vários algoritmos de otimização de segunda ordem que aproveitam essas informações, um dos quais é o método de Newton.

informações de segunda ordem, por outro lado, nos permite fazer uma aproximação quadrática da função objetiva e aproximar o tamanho do passo certo para atingir um mínimo local …

– Página 87, Algorithms for Optimization, 2019.

no caso univariado, o método de Newton usa uma expansão da série Taylor de segunda ordem para realizar a aproximação quadrática em torno de algum ponto da função objetiva. A regra de atualização para o método de Newton, que é obtida definindo a derivada como zero e resolvendo para a raiz, envolve uma operação de divisão pela segunda derivada. Se o método de Newton é estendido para otimização multivariada, a derivada é substituída pelo gradiente, enquanto o recíproco da segunda derivada é substituído pelo inverso da matriz hessiana.

estaremos cobrindo as aproximações das séries Hessian e Taylor, que alavancam o uso de derivativos de ordem superior, em tutoriais separados.

Leitura Adicional

esta seção fornece mais recursos sobre o tópico se você estiver procurando ir mais fundo.

livros

• cálculo único e multivariável, 2020.
• cálculo para Dummies, 2016.
• Aprendizagem Profunda, 2017.
• algoritmos para otimização, 2019.

resumo

neste tutorial, você descobriu como calcular derivadas univariadas e multivariadas de ordem superior.

especificamente, você aprendeu:

• como calcular as derivadas de ordem superior das funções univariadas.
• como calcular as derivadas de ordem superior de funções multivariadas.
• como as derivadas de segunda ordem podem ser exploradas no aprendizado de máquina por algoritmos de otimização de segunda ordem.