Instrumenty pochodne wyższego rzędu

Ostatnia aktualizacja: 21 lipca 2019 r.

instrumenty pochodne wyższego rzędu mogą przechwytywać informacje o funkcji, której same instrumenty pochodne pierwszego rzędu nie są w stanie przechwycić.

pochodne pierwszego rzędu mogą przechwytywać ważne informacje, takie jak szybkość zmian, ale same w sobie nie mogą odróżnić lokalnych minimów ani maksimów, gdzie szybkość zmian jest zerowa dla obu. Kilka algorytmów optymalizacyjnych rozwiązuje to ograniczenie poprzez wykorzystanie pochodnych wyższego rzędu, na przykład w metodzie Newtona, gdzie pochodne drugiego rzędu są używane do osiągnięcia lokalnego minimum funkcji optymalizacyjnej.

w tym samouczku dowiesz się, jak obliczyć jedno-i wielowymiarowe pochodne wyższego rzędu.

po ukończeniu tego kursu dowiesz się:

• Jak obliczyć pochodne wyższego rzędu funkcji univariate.
• jak obliczyć pochodne wyższego rzędu funkcji wielowymiarowych.
• jak można wykorzystać pochodne drugiego rzędu w uczeniu maszynowym przez algorytmy optymalizacji drugiego rzędu.

zaczynajmy.

opis poradnika

ten poradnik jest podzielony na trzy części; są to:

• pochodne wyższego rzędu funkcji wielowymiarowych
• pochodne wyższego rzędu funkcji wielowymiarowych
• zastosowanie w uczeniu maszynowym

pochodne wyższego rzędu funkcji jednowymiarowych

oprócz pochodnych pierwszego rzędu, które widzieliśmy, mogą dostarczyć nam ważnych informacji na temat funkcja, taka jak jej chwilowe tempo zmian, pochodne wyższego rzędu również mogą być równie użyteczne. Na przykład druga pochodna może mierzyć przyspieszenie poruszającego się obiektu lub może pomóc algorytmowi optymalizacji odróżnić lokalne maksimum od lokalnego minimum.

Obliczanie pochodnych funkcji univariate wyższego rzędu (drugiego, trzeciego lub wyższego) nie jest takie trudne.

druga pochodna funkcji jest po prostu pochodną jej pierwszej pochodnej. Trzecia pochodna jest pochodną drugiej pochodnej, czwarta pochodna jest pochodną trzeciej i tak dalej.

stąd obliczanie pochodnych wyższego rzędu polega po prostu na wielokrotnym różnicowaniu funkcji. Aby to zrobić, możemy po prostu zastosować naszą wiedzę na temat zasady władzy. Rozważmy funkcję, f (x) = x3 + 2×2 – 4x + 1, jako przykład. Następnie:

pierwsza pochodna: f'(x) = 3×2 + 4x – 4

druga pochodna: f”(x) = 6x + 4

trzecia pochodna: f”'(x) = 6

czwarta pochodna: f (4)(x) = 0

piąta pochodna: f (5)(x) = 0 itd.

to, co tutaj zrobiliśmy, to to, że najpierw zastosowaliśmy regułę mocy do f (x), aby otrzymać pierwszą pochodną, f'(x), następnie zastosowaliśmy regułę mocy do pierwszej pochodnej, aby uzyskać drugą, i tak dalej. Pochodna ostatecznie dojdzie do zera, ponieważ różnicowanie jest wielokrotnie stosowane.

zastosowanie reguł iloczynu i ilorazu również pozostaje ważne w otrzymywaniu pochodnych wyższego rzędu, ale ich obliczanie może stać się coraz bardziej messier wraz ze wzrostem rzędu. Ogólna reguła Leibniza upraszcza zadanie w tym aspekcie, uogólniając regułę produktu na:

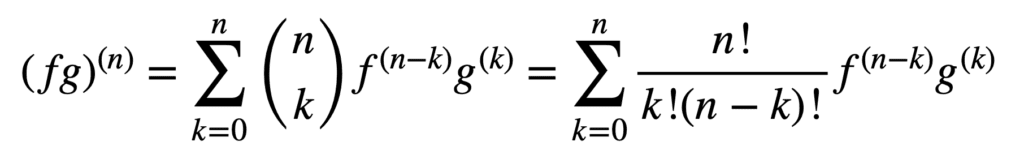
tutaj, termin, n! / k!(n-k)!, jest dwumianowym współczynnikiem z twierdzenia dwumianowego, podczas gdy f (k) i g (k) oznaczają pochodną kth funkcji, odpowiednio f I g.

zatem znalezienie pierwszej i drugiej pochodnej (a zatem podstawienie odpowiednio n = 1 i N = 2), zgodnie z ogólną zasadą Leibniza, daje nam:

(fg)(1) = (fg)’ = f (1) G + f g(1)

(FG) (2) = (fg)” = f(2) g + 2F(1) g (1) + F G (2)

zwróć uwagę na znaną pierwszą pochodną zdefiniowaną przez regułę produktu. Reguła Leibniza może być również użyta do znalezienia pochodnych wyższego rzędu funkcji racjonalnych, ponieważ iloraz może być skutecznie wyrażony w iloczyn postaci, f g-1.

pochodne cząstkowe funkcji wielowymiarowych wyższego rzędu

definicja pochodnych cząstkowych funkcji wielowymiarowych wyższego rzędu jest analogiczna do przypadku jednowymiarowego: pochodna cząstkowa n-tego rzędu dla n > 1 jest obliczana jako pochodna cząstkowa (n – 1)tej pochodnej cząstkowej. Na przykład, wzięcie drugiej pochodnej cząstkowej funkcji z dwiema zmiennymi daje cztery, drugie pochodne cząstkowe: dwie własne pochodne cząstkowe, fxx i fyy oraz dwie krzyżowe pochodne cząstkowe, fxy i fyx.

aby wziąć „pochodną”, musimy wziąć pochodną cząstkową względem x lub y, i są cztery sposoby, aby to zrobić: x wtedy X, X potem y, y potem x, y potem y.

– strona 371, rachunek jedno-i wielowymiarowy, 2020.

rozważmy funkcję wielowymiarową, f(x, y) = x2 + 3XY + 4y2, dla której chcielibyśmy znaleźć drugą pochodną cząstkową. Proces rozpoczyna się od znalezienia jego pochodnej cząstkowej pierwszego rzędu, najpierw: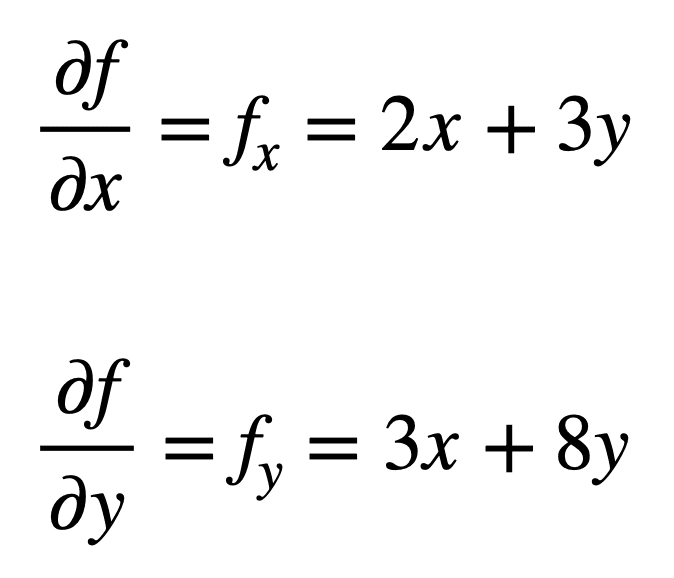

cztery pochodne cząstkowe drugiego rzędu są następnie znajdowane przez powtórzenie procesu znajdowania pochodnych cząstkowych, pochodnych cząstkowych. Własne pochodne cząstkowe są najprostsze do znalezienia, ponieważ po prostu powtarzamy proces różnicowania cząstkowego, w odniesieniu do x lub y, po raz drugi:

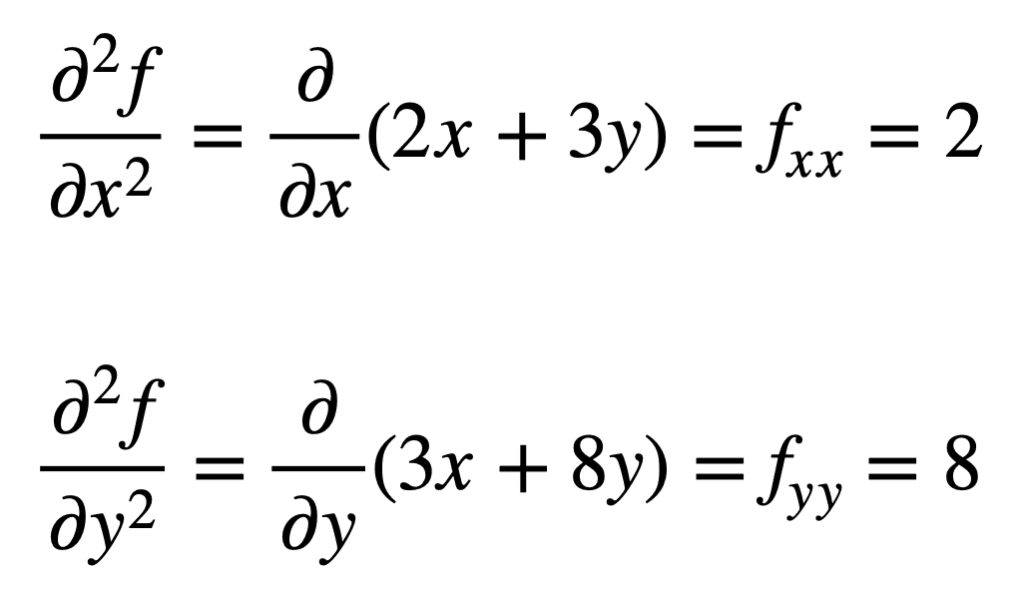
krzyżowa pochodna cząstkowa wcześniej znalezionego fx (czyli pochodna cząstkowa względem x) znajduje się poprzez wzięcie pochodnej cząstkowej wyniku względem y, dając nam fxy. Podobnie, biorąc pochodną cząstkową fy względem x, daje nam fyx:

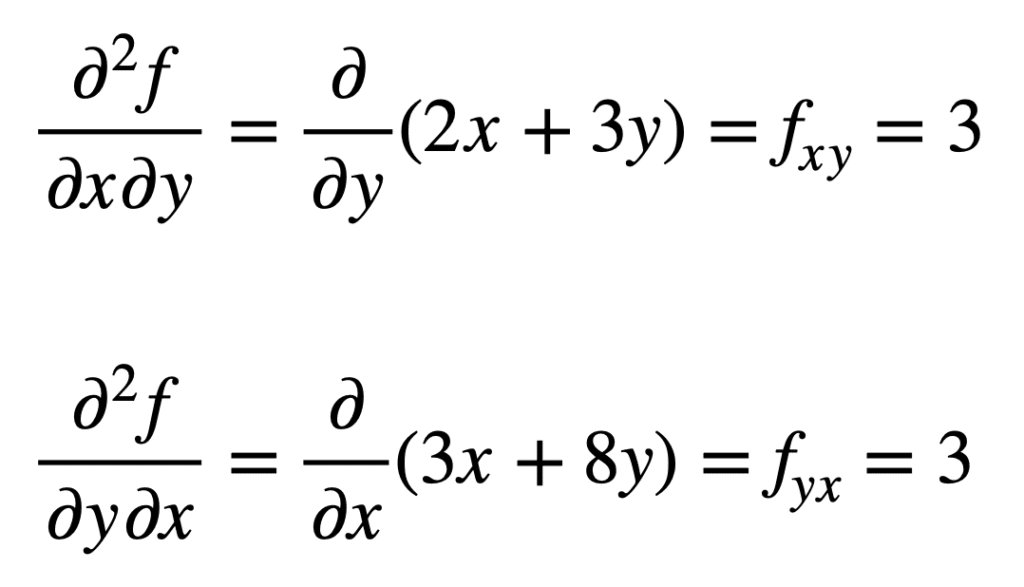
nie jest przypadkiem, że krzyżowe pochodne cząstkowe dają taki sam wynik. Jest to zdefiniowane przez twierdzenie Clairauta, które mówi, że dopóki pochodne cząstkowe są ciągłe, to są równe.

zastosowanie w uczeniu maszynowym

w uczeniu maszynowym jest to najczęściej używana pochodna drugiego rzędu. Wcześniej wspominaliśmy, że druga pochodna może dostarczyć nam informacji, których pierwsza pochodna sama w sobie nie może uchwycić. W szczególności, może nam powiedzieć, czy punkt krytyczny jest lokalnym minimum lub maksimum (w oparciu o to, czy druga pochodna jest większa lub mniejsza od zera, odpowiednio), dla których pierwsza pochodna, w przeciwnym razie, byłaby Zerowa W obu przypadkach.

istnieje kilka algorytmów optymalizacji drugiego rzędu, które wykorzystują te informacje, jednym z nich jest Metoda Newtona.

z drugiej strony informacje drugiego rzędu pozwalają nam na kwadratowe przybliżenie funkcji celu i przybliżenie odpowiedniego rozmiaru kroku, aby osiągnąć lokalne minimum …

-strona 87, algorytmy optymalizacji, 2019.

w przypadku jednowymiarowym Metoda Newtona wykorzystuje rozszerzenie szeregów Taylora drugiego rzędu do wykonania aproksymacji kwadratowej wokół pewnego punktu funkcji celu. Reguła aktualizacji dla metody Newtona, którą otrzymuje się przez ustawienie pochodnej na zero i rozwiązanie dla pierwiastka, polega na operacji dzielenia przez drugą pochodną. Jeśli Metoda Newtona zostanie rozszerzona na optymalizację wielowymiarową, pochodna zostanie zastąpiona gradientem, natomiast odwrotność drugiej pochodnej zostanie zastąpiona odwrotnością macierzy Hesa.

będziemy omawiać przybliżenia serii Hessian i Taylor, które wykorzystują użycie pochodnych wyższego rzędu, w oddzielnych samouczkach.

Czytaj dalej

Ta sekcja zawiera więcej zasobów na ten temat, jeśli chcesz zagłębić się w ten temat.

Książki

• rachunek jedno-i wielowymiarowy, 2020.
• Deep Learning, 2017.
• algorytmy optymalizacji, 2019.

podsumowanie

w tym samouczku odkryłeś, jak obliczyć jedno-i wielowymiarowe pochodne wyższego rzędu.

konkretnie, nauczyłeś się:

• Jak obliczyć pochodne wyższego rzędu funkcji univariate.
• jak obliczyć pochodne wyższego rzędu funkcji wielowymiarowych.
• jak można wykorzystać pochodne drugiego rzędu w uczeniu maszynowym przez algorytmy optymalizacji drugiego rzędu.