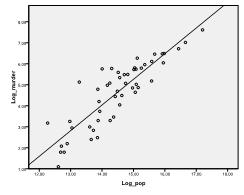
ten przykład opiera się na statystyce przestępczości FBI z 2006 roku. Szczególnie interesuje nas związek między wielkością państwa a liczbą morderstw w mieście.
najpierw musimy sprawdzić, czy w danych występuje zależność liniowa. W tym celu sprawdzamy Plan rozproszenia. Wykres punktowy wskazuje na dobrą zależność liniową, co pozwala na przeprowadzenie analizy regresji liniowej. Możemy również sprawdzić Dwumienną korelację Pearsona i stwierdzić, że obie zmienne są silnie skorelowane (r = .959 z p < 0, 001).

dowiedz się, jak pomagamy edytować rozdziały dysertacji
wyrównywanie ram teoretycznych, zbieranie artykułów, syntetyzowanie luk, formułowanie jasnej metodologii i planu danych oraz pisanie o teoretycznych i praktycznych implikacjach badań są częścią naszych kompleksowych usług edycji dysertacji.
- doprowadzić rozprawa editing expertise do rozdziałów 1-5 w odpowiednim czasie.
- Śledź wszystkie zmiany, a następnie współpracuj z Tobą, aby doprowadzić do pisania naukowego.
- bieżące wsparcie w odniesieniu do opinii Komitetu, zmniejszanie zmian.
po drugie, musimy sprawdzić wielowymiarową normalność. W naszym przykładzie stwierdzamy, że wielowymiarowa normalność może nie być obecna.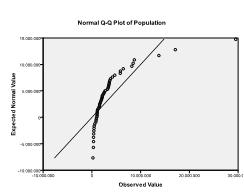
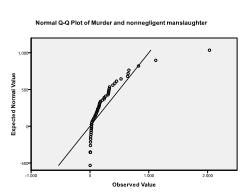
test Kołmogorowa-Smirnowa potwierdza to podejrzenie (p = 0,002 i p = 0.006). Przeprowadzenie transformacji ln na dwóch zmiennych rozwiązuje problem i ustanawia wielowymiarową normalność (test K-S P=.991 i p = .543).
teraz możemy przeprowadzić analizę regresji liniowej. Regresja liniowa znajduje się w SPSS w Analyze / Regression / Linear…
w tym prostym przypadku musimy po prostu dodać zmienne log_pop i log_murder do modelu jako zmienne zależne i niezależne.
statystyki terenowe pozwalają nam uwzględnić dodatkowe statystyki, które są nam potrzebne do oceny poprawności naszej analizy regresji liniowej.
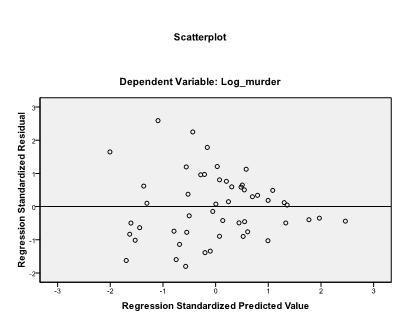
zaleca się dodatkowo włączenie diagnostyki kolinearności i testu Durbina-Watsona do automatycznej korelacji. Aby przetestować założenie homoscedastyczności pozostałości, w menu działki zamieszczamy również specjalny Wykres.
składnia SPSS dla analizy regresji liniowej to
regresja
/ MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL
/ CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT Log_murder
/METHOD=ENTER Log_pop
/SCATTERPLOT=(*ZERID ,*ZPRED)
/RESIDUALS DURBIN HIST(ZERID).
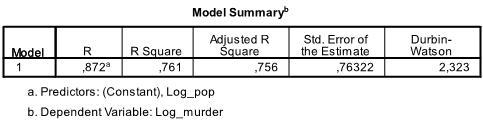
pierwsza tabela wyników pokazuje podsumowanie modelu i ogólne statystyki dopasowania. Okazuje się, że skorygowany R2 naszego modelu wynosi 0,756 z R2 =.761 oznacza to, że regresja liniowa wyjaśnia 76.1% wariancji danych. Durbin-Watson d = 2,323, który znajduje się pomiędzy dwiema wartościami krytycznymi 1,5 < d < 2,5 i dlatego możemy założyć, że w danych nie ma automatycznej korelacji liniowej pierwszego rzędu.
Następna tabela jest F-test, F-test regresji liniowej ma hipotezę zerową, że nie ma liniowej zależności między dwoma zmiennymi (innymi słowy R2=0). Z F = 156.2 i 50 stopni swobody test jest bardzo istotny, dlatego możemy założyć, że istnieje liniowa zależność między zmiennymi w naszym modelu.


Następna tabela pokazuje współczynniki regresji, punkt przecięcia i znaczenie wszystkich współczynników oraz punkt przecięcia w modelu. Okazuje się, że nasza analiza regresji liniowej szacuje funkcję regresji liniowej na y = -13,067 + 1,222
* x. należy pamiętać, że nie przekłada się to na 1.2 dodatkowe morderstwa na każde 1000 dodatkowych mieszkańców, ponieważ zmieniliśmy zmienne.
gdybyśmy ponownie przeprowadzili analizę regresji liniowej z oryginalnymi zmiennymi, skończylibyśmy z y = 11.85 + 6.7*10-5 co pokazuje, że na każde 10 000 dodatkowych mieszkańców spodziewamy się 6,7 dodatkowych morderstw.
w naszej analizie regresji liniowej test sprawdza hipotezę zerową, że współczynnik wynosi 0. Test t stwierdza, że zarówno intercept, jak i zmienna są bardzo znaczące (p < 0,001) i dlatego możemy powiedzieć, że są różne od zera.

ta tabela zawiera również wagi Beta (które wyrażają względne znaczenie zmiennych niezależnych) i statystyki koliniowości. Ponieważ jednak w naszej analizie mamy tylko 1 zmienną niezależną, nie zwracamy uwagi na te wartości.
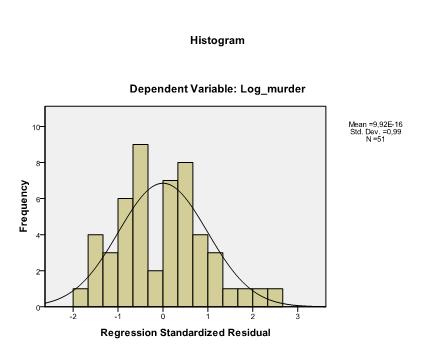
ostatnią rzeczą, którą musimy sprawdzić, jest homoscedastyczność i normalność pozostałości. Histogram wskazuje, że pozostałości przybliżają rozkład normalny. Wykres Q-Q z * pred i z * presid pokazuje nam, że w naszej analizie regresji liniowej nie ma tendencji w kategoriach błędów.