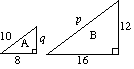een vergroting is een transformatie waarbij een object een afbeelding afbeeldt met dezelfde vorm maar een andere grootte. Het object en de afbeelding lijken op elkaar. Een uitbreiding vereist een centrum van uitbreiding en een schaalfactor.
Notatie
E is een uitbreiding, met het centrum van de uitbreiding O en schaal factor µ.
E: AB 
AB
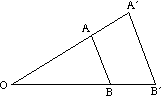
eigenschappen van uitbreiding
driehoek PQR kaarten naar driehoek PQR onder uitbreiding met Centrum O.
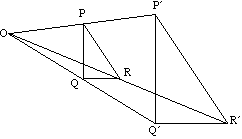
lijnen en hun beelden zijn altijd parallel.
bijv. PQ is parallel aan PQ
hoekgrootte is invariant.
bijv.
PQR =
het centrum van de uitbreiding is het enige invariante punt.
lengte en oppervlakte zijn niet invariant, behalve wanneer m = 1 of − 1.
d.w.z. vergroting is geen isometrie.
uitbreiding is een directe transformatie.
d.w.z.
PQR en
indien μ de schaalfactor voor lengte is, is mµ 2 de schaalfactor voor het oppervlak.
verschillende schaalfactoren
het onderstaande diagram toont het effect van verschillende schaalfactoren op de vergroting van een driehoek ABC rond het centrum O.
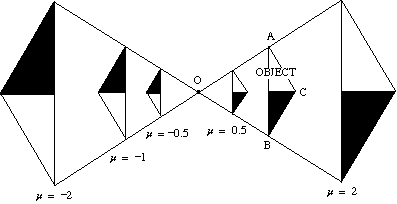
- als de schaalfactor positief is, liggen zowel het object als het beeld aan dezelfde kant van het centrum.
- als de schaalfactor negatief is, bevinden het object en het beeld zich aan weerszijden van het midden.
de afbeelding is omgekeerd.
zie voorbeelden van uitbreidingen− 
locatie van het centrum van de uitbreiding
gegeven een figuur en het beeld, om het centrum van de uitbreiding te vinden:
1. Voeg een punt en zijn imago samen.
2. Herhaal voor een ander punt en zijn afbeelding.
3. Het centrum van de uitbreiding is het snijpunt van deze lijnen.
soortgelijke figuren
figuren zijn gelijkaardig indien zij dezelfde vorm hebben.
- soortgelijke cijfers kunnen op elkaar worden afgebeeld door een vergroting of door een combinatie van reflectie, rotatie of vertaling en een vergroting.
- de overeenkomstige hoeken van soortgelijke cijfers zijn gelijk.
- de overeenkomstige zijden zijn evenredig met elkaar.
Type 1
YXZ is gelijk aan PQM omdat zij overeenkomstige hoeken gelijk hebben.
|
|
 |
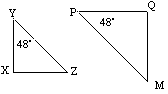YXZ kan worden toegewezen aan PQM door een combinatie van transformaties.
schaalfactor = µ = 
Type 2
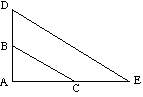
ABC is vergelijkbaar met ADE omdat:
|
(de is parallel aan BC) |
 |
ABC kan door een vergroting op ADE worden toegewezen.
schaalfactor = µ = 
|
(a) (i) de twee driehoeken A en B zijn vergelijkbaar. Zoek p en q. |
(a) i) voor A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii)de oppervlakte van driehoek A is 24 units2. |
(ii) schaalfactor voor oppervlakte = µ2 = 4 Oppervlakte van driehoek B = 4 x oppervlakte van driehoek A |
|
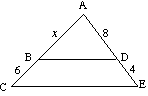
(b) Bereken x, als BD evenwijdig aan CE |
(b) Voor
  12x = 8(x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B , schaalfactor = 2
ABD
Download een interactief werkblad (Microsoft Excel) met spiegelingen, rotaties, translaties en uitbreidingen.
(Windows-gebruikers, Klik met de rechtermuisknop en ” Doel opslaan als…”om de bestanden op uw computer op te slaan.)
