dette eksemplet er basert PÅ FBIS kriminalstatistikk fra 2006. Spesielt er vi interessert i forholdet mellom statens størrelse og antall mord i byen.
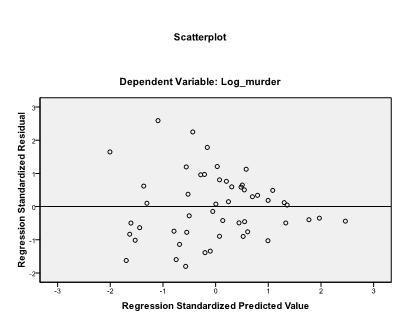
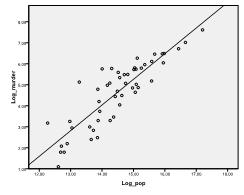
først må Vi sjekke om det er et lineært forhold i dataene. For det sjekker vi scatterplot. Scatter-plottet indikerer et godt lineært forhold, noe som gjør at vi kan utføre en lineær regresjonsanalyse. Vi kan også sjekke Pearsons Bivariate Korrelasjon og finne at begge variablene er svært korrelerte (r = .959 med p < 0,001).

Oppdag Hvordan Vi Hjelper Til Med Å Redigere Avhandlingskapitlene
Justere teoretisk rammeverk, samle artikler, syntetisere hull, formulere en klar metodikk og dataplan, og skrive om de teoretiske og praktiske implikasjonene av forskningen din er en del av våre omfattende avhandlingsredigeringstjenester.
- Ta med avhandlingsredigeringskompetanse til kapittel 1-5 i tide.
- Spor alle endringer, og arbeid med deg for å få vitenskapelig skriving.
- Løpende støtte for å adressere komiteens tilbakemelding, redusere revisjoner.
For det Andre må vi sjekke for multivariate normalitet. I vårt eksempel finner vi at multivariat normalitet kanskje ikke er til stede.
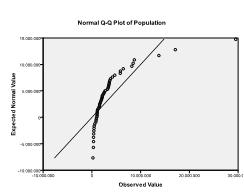
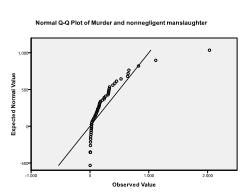
Kolmogorov-Smirnov-testen bekrefter denne mistanken (p = 0,002 og p = 0.006). Gjennomføring av en ln-transformasjon på de to variablene løser problemet og etablerer multivariat normalitet (Ks test p =.991 og p = .543).
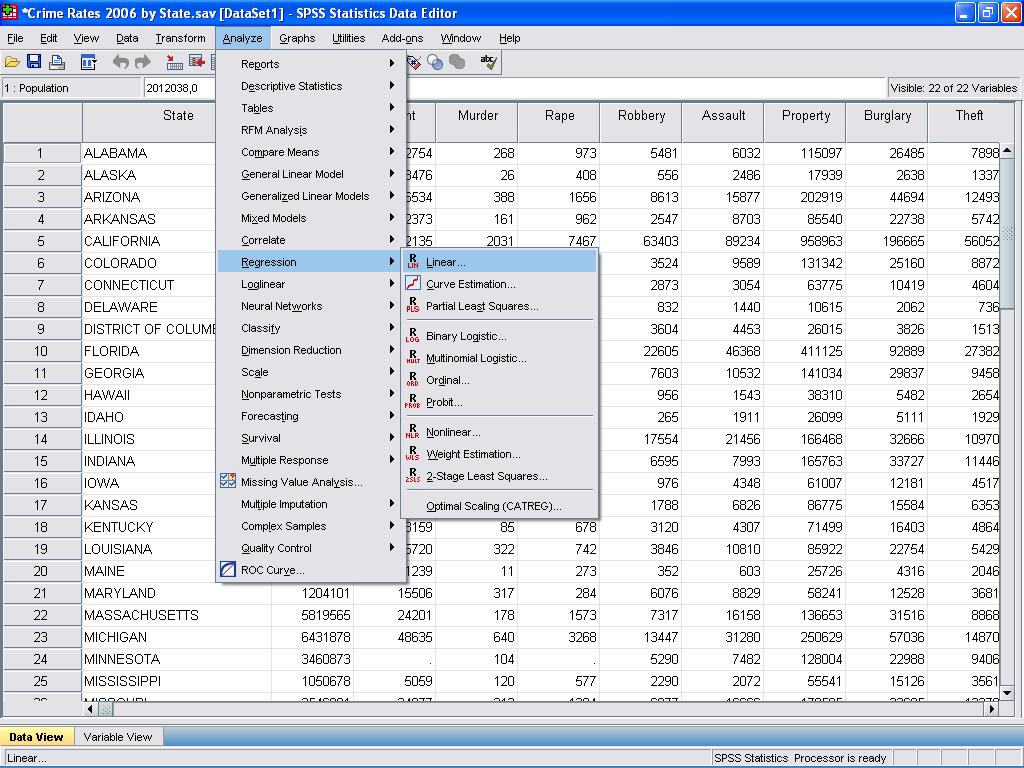
vi kan nå gjennomføre den lineære regresjonsanalysen. Lineær regresjon er funnet I Spss I Analyse / Regresjon / Lineær…
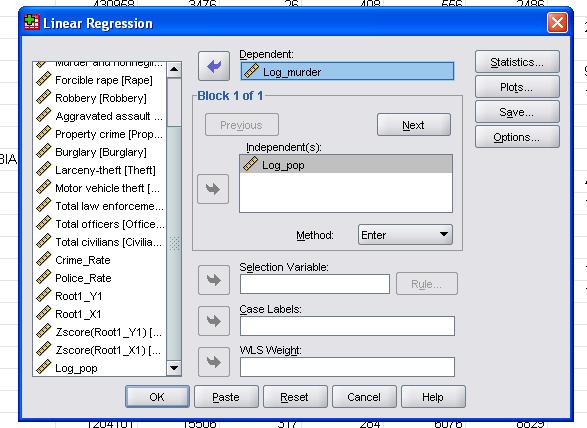
i dette enkle tilfellet må vi bare legge til variablene log_pop og log_murder til modellen som avhengige og uavhengige variabler.
feltstatistikken tillater oss å inkludere tilleggsstatistikk som vi trenger for å vurdere gyldigheten av vår lineære regresjonsanalyse.
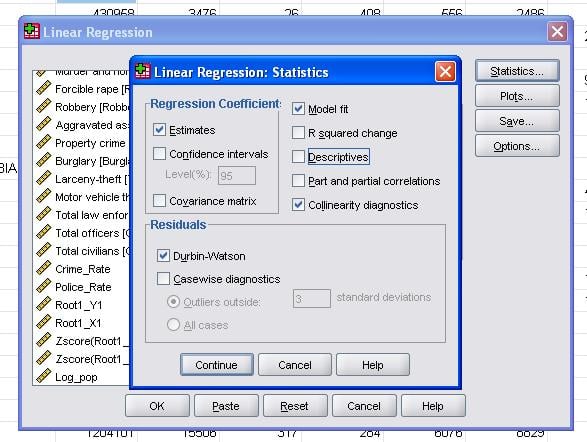
det er tilrådelig å i tillegg inkludere kollinearitetsdiagnostikken og Durbin-Watson-testen for automatisk korrelasjon. For å teste antagelsen om homoscedasticity av residuals inkluderer vi også en spesiell tomt i Plott-menyen.
Spss-Syntaksen for den lineære regresjonsanalysen er
REGRESJON
/ MANGLENDE LISTWISE
/ STATISTIKK COEFF OUTS R ANOVA COLLIN TOL
/ KRITERIER = PIN(.05) SURMULE(.10)
/ NOORIGIN
/ AVHENGIG Log_murder
/ METODE = SKRIV Inn Log_pop
/ SCATTERPLOT=(*ZRESID, * ZPRED)
/ RESTER DURBIN HIST (ZRESID).
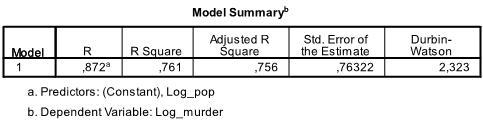
utdataens første tabell viser modellsammendrag og samlet fit-statistikk. Vi finner at den justerte R2 av vår modell er 0,756 med R2 = .761 det betyr at den lineære regresjonen forklarer 76.1% av variansen i dataene. Durbin-Watson d = 2.323, som er mellom de to kritiske verdiene på 1.5 < d < 2.5, og derfor kan vi anta at det ikke er noen første ordens lineær auto-korrelasjon i dataene.
neste tabell er F-testen, den lineære regresjonens F-test har nullhypotesen om at det ikke er noe lineært forhold mellom de to variablene (med Andre ord R2=0). F = 156.2 og 50 frihetsgrader testen er svært viktig, og dermed kan vi anta at det er et lineært forhold mellom variablene i vår modell.


neste tabell viser regresjonskoeffisientene, skjæringspunktet og betydningen av alle koeffisientene og skjæringspunktet i modellen. Vi finner at vår lineære regresjonsanalyse anslår den lineære regresjonsfunksjonen til å være y = -13.067 + 1.222
* x. Vær oppmerksom på at dette ikke oversetter der er 1.2 ekstra mord for hver 1000 ekstra innbyggere fordi vi ln forvandlet variablene.
hvis vi kjørte den lineære regresjonsanalysen med de opprinnelige variablene, ville vi ende opp med y = 11.85 + 6.7*10-5 som viser at for hver 10.000 ekstra innbyggere forventer vi å se 6,7 flere mord.
i vår lineære regresjonsanalyse tester testen nullhypotesen om at koeffisienten er 0. T-testen finner at både intercept og variable er svært signifikante (p < 0,001), og dermed kan vi si at de er forskjellige fra null.

denne tabellen inneholder Også Betavektene (som uttrykker den relative betydningen av uavhengige variabler) og kollinearitetsstatistikken. Men siden vi bare har 1 uavhengig variabel i vår analyse, tar vi ikke hensyn til disse verdiene.
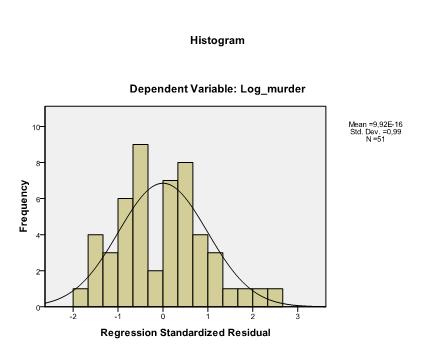
det siste vi må sjekke er homoskedastisitet og normalitet av rester. Histogrammet indikerer at residualene omtrentlig en normalfordeling. Q-Q-Plottet til z * pred og z*presid viser oss at i vår lineære regresjonsanalyse er det ingen tendens i feilbetingelsene.