Cet exemple est basé sur les statistiques de la criminalité de 2006 du FBI. Nous nous intéressons particulièrement à la relation entre la taille de l’État et le nombre de meurtres dans la ville.
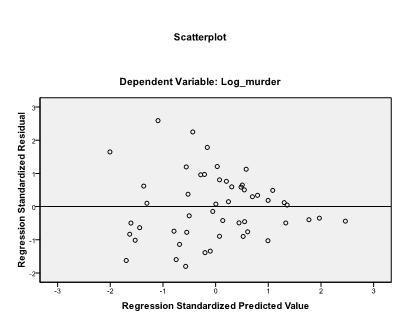
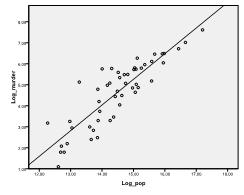
Nous devons d’abord vérifier s’il existe une relation linéaire dans les données. Pour cela, nous vérifions le nuage de points. Le nuage de points indique une bonne relation linéaire, ce qui nous permet d’effectuer une analyse de régression linéaire. Nous pouvons également vérifier la corrélation bivariée de Pearson et constater que les deux variables sont fortement corrélées (r =.959 avec p < 0,001).

Découvrez comment Nous vous aidons à éditer vos chapitres de thèse
Aligner le cadre théorique, rassembler des articles, synthétiser les lacunes, articuler une méthodologie et un plan de données clairs et écrire sur les implications théoriques et pratiques de votre recherche font partie de nos services complets d’édition de thèse.
- Apportez une expertise en édition de thèse aux chapitres 1 à 5 en temps opportun.
- Suivez tous les changements, puis travaillez avec vous pour apporter une écriture savante.
- Soutien continu pour répondre aux commentaires des comités, réduisant ainsi les révisions.
Deuxièmement, nous devons vérifier la normalité multivariée. Dans notre exemple, nous constatons que la normalité multivariée pourrait ne pas être présente.
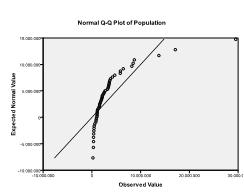
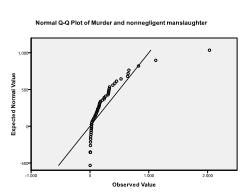
Le test de Kolmogorov-Smirnov confirme cette suspicion (p = 0,002 et p = 0.006). Effectuer une transformation ln sur les deux variables résout le problème et établit une normalité multivariée (test K-S p =.991 et p =.543).
Nous pouvons maintenant effectuer l’analyse de régression linéaire. La régression linéaire se trouve dans SPSS dans Analyser / Régression / Linéaire…
Dans ce cas simple, nous devons simplement ajouter les variables log_pop et log_murder au modèle en tant que variables dépendantes et indépendantes.
Les statistiques de terrain nous permettent d’inclure des statistiques supplémentaires dont nous avons besoin pour évaluer la validité de notre analyse de régression linéaire.
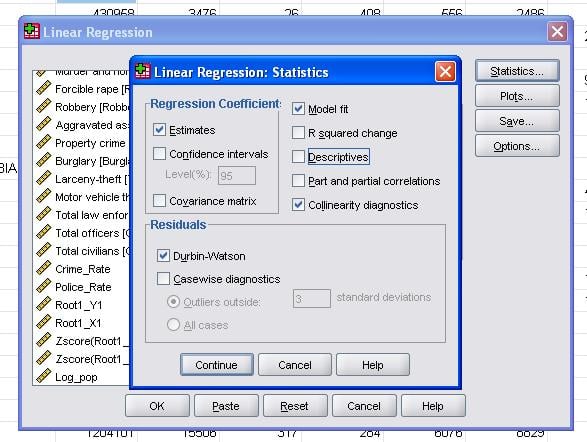
Il est conseillé d’inclure en plus le diagnostic de colinéarité et le test de Durbin-Watson pour l’auto-corrélation. Pour tester l’hypothèse de l’homoscédasticité des résidus, nous incluons également un tracé spécial dans le menu des tracés.
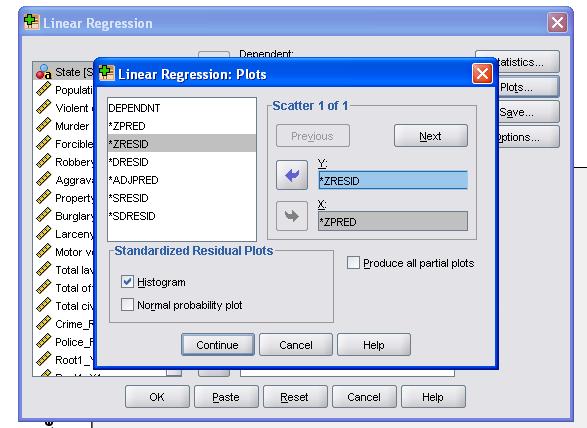
La syntaxe SPSS pour l’analyse de régression linéaire est
RÉGRESSION
/ LISTE MANQUANTE
/ STATISTIQUES COEFF OUTS R ANOVA COLLIN TOL
/ CRITERIA= PIN(.05) MOUE (.10)
/ NOORIGIN
/ DEPENDENT Log_murder
/METHOD = ENTER Log_pop
/ SCATTERPLOT =(*ZRESID, *ZPRED)
/ RÉSIDUS DURBIN HIST(ZRESID).
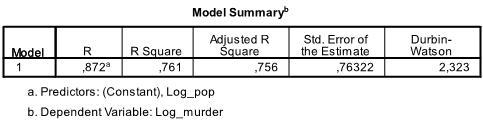
Le premier tableau de la sortie affiche le résumé du modèle et les statistiques d’ajustement globales. Nous constatons que le R2 ajusté de notre modèle est de 0,756 avec le R2 =.761 cela signifie que la régression linéaire explique 76.1% de la variance des données. Le Durbin-Watson d = 2,323, qui est entre les deux valeurs critiques de 1,5 < d < 2,5 et nous pouvons donc supposer qu’il n’y a pas d’auto-corrélation linéaire du premier ordre dans les données.
Le tableau suivant est le test F, le test F de la régression linéaire a l’hypothèse nulle qu’il n’y a pas de relation linéaire entre les deux variables (en d’autres termes R2 = 0). Avec F = 156.2 et 50 degrés de liberté le test est très significatif, nous pouvons donc supposer qu’il existe une relation linéaire entre les variables de notre modèle.


Le tableau suivant montre les coefficients de régression, l’ordonnée à l’origine et la signification de tous les coefficients et de l’ordonnée à l’origine dans le modèle. Nous constatons que notre analyse de régression linéaire estime la fonction de régression linéaire à y = -13,067 + 1,222
* x. Veuillez noter que cela ne se traduit pas par 1.2 meurtres supplémentaires pour 1000 habitants supplémentaires car nous avons transformé les variables.
Si nous relions l’analyse de régression linéaire avec les variables d’origine, nous nous retrouverions avec y = 11.85 + 6.7*10-5 ce qui montre que pour 10 000 habitants supplémentaires, nous nous attendrions à voir 6,7 meurtres supplémentaires.
Dans notre analyse de régression linéaire, le test teste l’hypothèse nulle que le coefficient est 0. Le test t révèle que l’ordonnée à l’origine et la variable sont très significatives (p < 0,001) et nous pourrions donc dire qu’elles sont différentes de zéro.

Ce tableau comprend également les poids bêta (qui expriment l’importance relative des variables indépendantes) et les statistiques de colinéarité. Cependant, comme nous n’avons qu’une seule variable indépendante dans notre analyse, nous ne prêtons pas attention à ces valeurs.
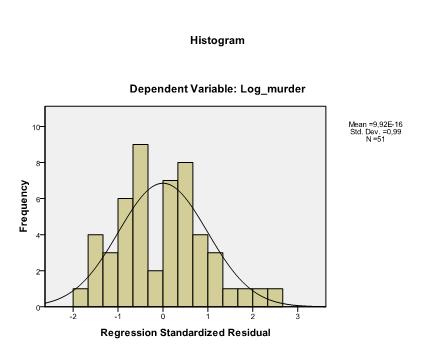
La dernière chose que nous devons vérifier est l’homoscédasticité et la normalité des résidus. L’histogramme indique que les résidus se rapprochent d’une distribution normale. Le graphique Q-Q de z * pred et z * presid nous montre que dans notre analyse de régression linéaire, il n’y a pas de tendance dans les termes d’erreur.