고차 파생 상품

2021 년 7 월 31 일 최종 업데이트

고차 파생 상품은 1 차 파생 상품이 자체적으로 캡처 할 수없는 기능에 대한 정보를 캡처 할 수 있습니다.

1 차 파생 상품은 변화율과 같은 중요한 정보를 캡처 할 수 있지만,그 자체로는 지역 최소값 또는 최대 값을 구별 할 수 없으며,여기서 변화율은 둘 다 0 입니다. 여러 최적화 알고리즘 2 차 파생 상품 최적화 함수의 로컬 최소 도달 하는 데 사용 되는 뉴턴의 방법에서와 같이 높은 차 파생 상품의 사용을 이용 하 여이 제한을 해결 합니다.

이 자습서에서는 고차 일변량 및 다변량 도함수를 계산하는 방법을 알아봅니다.

이 자습서를 완료하면 알 수 있습니다:

• 단 변량 함수의 고차 미분을 계산하는 방법.
• 다변량 함수의 고차 도함수를 계산하는 방법.
• 2 차 유도체가 2 차 최적화 알고리즘에 의해 기계 학습에서 어떻게 악용 될 수 있는지.

시작하자.

자습서 개요

이 자습서는 세 부분으로 나뉩니다.:

• 단변량 함수의 고차 유도체
• 다변량 함수의 고차 유도체
• 기계 학습에서의 응용

단변량 함수의 고차 유도체

우리가 본 1 차 유도체 외에도 함수에 대한 중요한 정보를 제공 할 수 있습니다.,이러한 변화의 순간 속도로,고차 파생 상품도 똑같이 유용 할 수 있습니다. 예를 들어,제 2 도함수는 움직이는 물체의 가속도를 측정 할 수 있거나 최적화 알고리즘이 로컬 최대 값과 로컬 최소값을 구별하는 데 도움이 될 수 있습니다.

단변량 함수의 고차(제 2,제 3 또는 그 이상)도함수를 계산하는 것은 그리 어렵지 않다.

함수의 두 번째 미분은 첫 번째 미분의 미분 일뿐입니다. 세 번째 파생 상품은 두 번째 파생 상품의 파생 상품이며,네 번째 파생 상품은 세 번째 파생 상품 등입니다.

–페이지 147,인형을위한 미적분학,2016.

따라서 고차 도함수를 계산하는 것은 단순히 함수를 반복적으로 차별화하는 것을 포함합니다. 그렇게하기 위해 우리는 단순히 권력 규칙에 대한 지식을 적용 할 수 있습니다. 이 함수에는 두 가지 유형이 있습니다. 1 차 미분법에서 파생 된 첫 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 두 번째 미분법에서 파생 된 0 등

우리가 여기서 한 일은 먼저 제곱 규칙을 에프(엑스)에 적용하여 첫 번째 미분,에프(엑스)을 얻은 다음 두 번째를 얻기 위해 제곱 규칙을 첫 번째 미분에 적용한 것입니다. 차별화가 반복적으로 적용되면 파생 상품은 결국 0 으로 이동합니다.

제품 및 몫 규칙의 적용은 또한 고차 파생 상품을 얻는 데 여전히 유효하지만,그 계산은 순서가 증가함에 따라 더 지저분 해지고 더 지저분해질 수 있습니다. 일반 라이프니츠 규칙은 제품 규칙을 일반화하여 이러한 측면에서 작업을 단순화합니다:

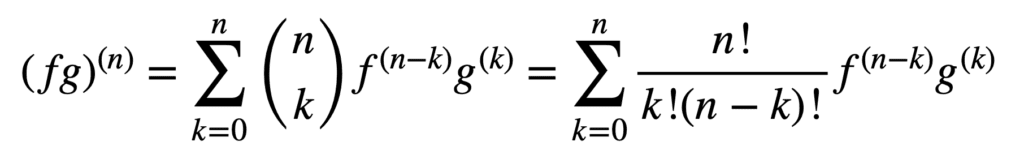
여기,용어,엔! /케이!(엔–케이)!,이다 이항 계수…에서 이항 정리,동안 에프(케이)과 지(케이)는 케티 함수의 도함수,에프 과 지,각각.

따라서 일반 라이프니츠 규칙에 의해 첫 번째와 두 번째 파생 상품(따라서 엔=1 과 엔=2 를 각각 대체)을 찾는 것은 우리에게:

(에프)(1)=(에프)’=에프(1)(1)

(1 차 도함수(2)=2 차 도함수(2)=2 차 도함수(1)지(1)+에프 지(2)

곱 규칙에 의해 정의된 친숙한 제 1 도함수를 주목하라. 라이프니츠 규칙은 또한 합리적인 함수의 고차 파생 상품을 찾는 데 사용될 수 있습니다.

다변량 함수의 고차 도함수

다변량 함수의 고차 부분 도함수의 정의는 단변량 경우와 유사합니다: 그만큼 엔 차 부분 미분 에 대한 엔>1,의 부분 미분(엔–1)번째 순서 부분 미분. 예를 들어,두 개의 변수가있는 함수의 두 번째 부분 도함수를 취하면 두 개의 자체 부분 도함수 인 두 개의 부분 도함수와 두 개의 교차 부분 도함수 인 두 개의 부분 도함수가 생성됩니다.

“미분”을 취하려면 부분 미분을 취해야합니다 엑스 또는 와이,그리고 네 가지 방법이 있습니다.

다변량 함수를 고려해 보겠습니다. 이 과정은 첫 번째 순서 부분 파생 상품을 찾는 것으로 시작합니다: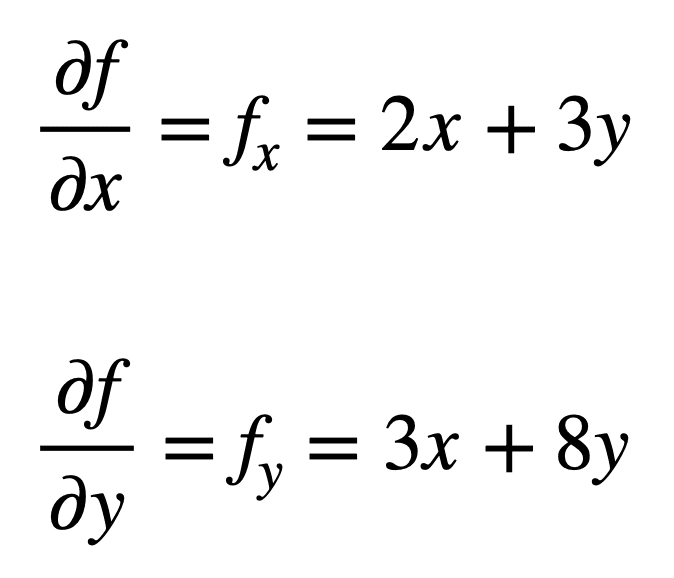

4,2 차 부분 파생 상품은 다음 부분 파생 상품의 부분 파생 상품을 찾는 과정을 반복 하 여 발견 됩니다. 자신의 부분 파생 상품은 찾기 위해 가장 간단합니다,우리는 단순히 부분 차별화 과정을 반복하기 때문에,중 하나에 대한 엑스 또는 와이,두 번째 시간:

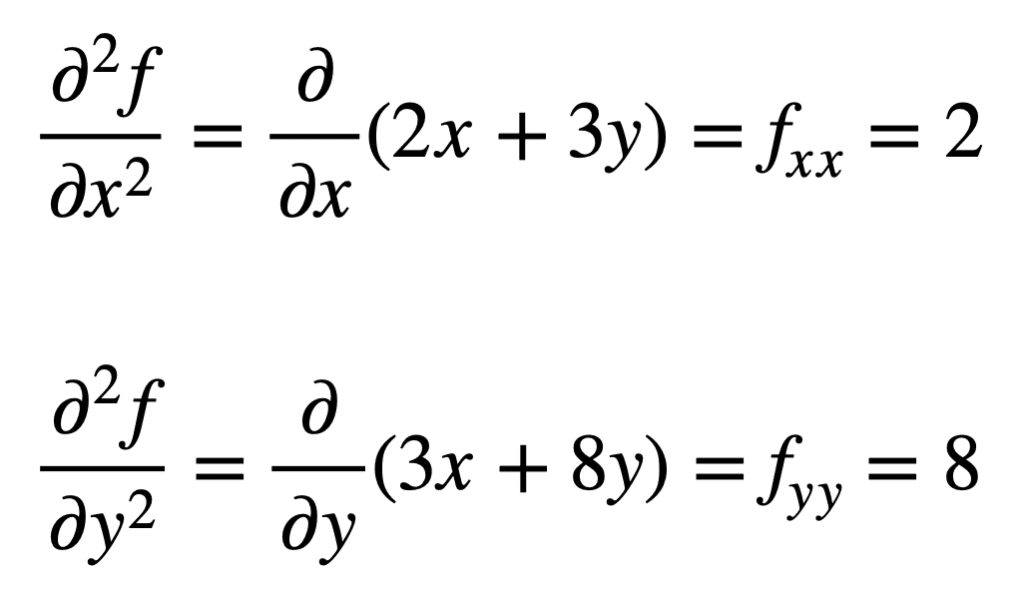
이전에 발견 된 외환의 교차 부분 도함수(즉,에 대한 부분 도함수 엑스)는 결과의 부분 도함수를 취함으로써 발견됩니다 와이,우리에게 외환을주십시오. 마찬가지로,에 대한 회계 연도의 부분 도함수를 취 엑스,우리에게 픽스 제공:

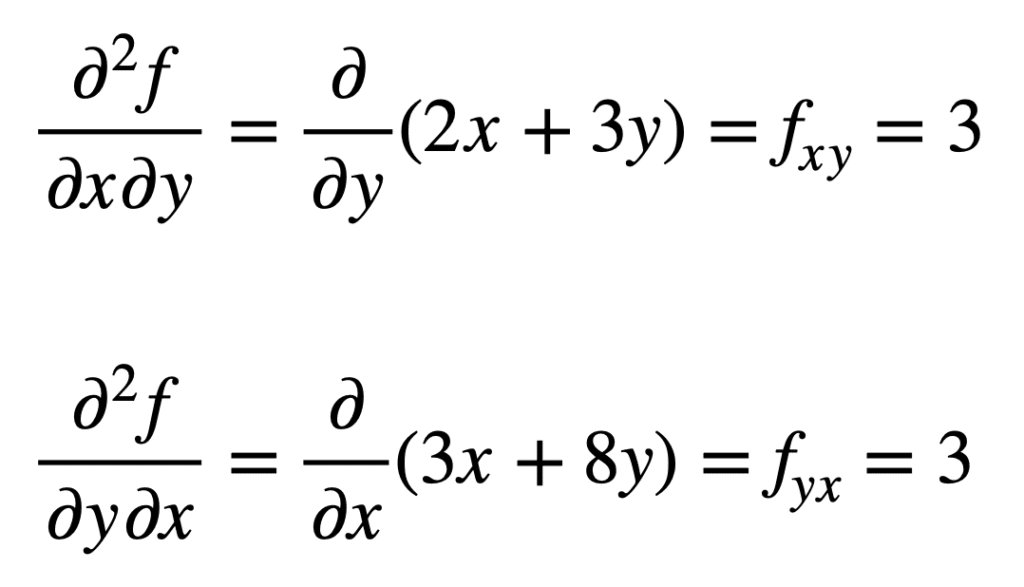
교차 부분 파생 상품이 동일한 결과를 제공하는 것은 우연이 아닙니다. 이것은 클라이 루트의 정리에 의해 정의되며,교차 부분 파생물이 연속적 인 한 그들은 동등하다는 것을 명시합니다.

기계 학습의 응용

기계 학습에서는 주로 사용되는 2 차 파생물입니다. 우리는 이전에 제 2 미분 자체가 캡처 할 수없는 정보를 우리에게 제공 할 수 있음을 언급했다. 특히,임계점이 로컬 최소 또는 최대인지 여부를 알 수 있습니다(두 번째 미분이 각각 0 보다 크거나 작은지 여부에 따라).이 경우 첫 번째 미분은 그렇지 않으면 두 경우 모두 0 이됩니다.

이 정보를 활용하는 몇 가지 2 차 최적화 알고리즘이 있으며 그 중 하나는 뉴턴의 방법입니다.

반면에 2 차 정보는 목적 함수의 2 차 근사치를 만들고 올바른 단계 크기를 근사하여 로컬 최소값에 도달 할 수있게합니다…

-페이지 87,최적화 알고리즘,2019.

단변량 사례에서 뉴턴의 방법은 2 차 테일러 시리즈 확장을 사용하여 목적 함수의 일부 지점 주변의 2 차 근사치를 수행합니다. 도함수를 0 으로 설정하고 루트에 대해 해결함으로써 얻어지는 뉴턴의 방법에 대한 업데이트 규칙은 두 번째 도함수에 의한 나누기 연산을 포함합니다. 뉴턴의 방법이 다변량 최적화로 확장되면,도함수는 그라데이션으로 대체되고,제 2 도함수의 역수는 헤센 행렬의 역수로 대체됩니다.

우리는 별도의 자습서에서 고차 파생 상품의 사용을 활용하는 헤센 및 테일러 시리즈 근사치를 다룰 것입니다.

추가 읽기

이 섹션에서는 좀 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

도서

• 단일 및 다 변수 미적분학,2020.
• 인형을위한 미적분학,2016.
• 딥 러닝,2017.
• 최적화 알고리즘,2019.

요약

이 자습서에서는 고차 일변량 및 다변량 도함수를 계산하는 방법을 발견했습니다.

구체적으로,당신은 배웠습니다:

• 단 변량 함수의 고차 미분을 계산하는 방법.
• 다변량 함수의 고차 도함수를 계산하는 방법.
• 2 차 유도체가 2 차 최적화 알고리즘에 의해 기계 학습에서 어떻게 악용 될 수 있는지.