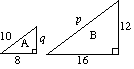拡大とは、オブジェクトが同じ形状でサイズが異なる画像にマップされる変換です。 オブジェクトと画像は類似していると言われています。 拡大には、拡大の中心とスケール係数が必要です。
表記
Eは拡大であり、拡大の中心はOでスケール係数はμである。
E:AB![]() AB
AB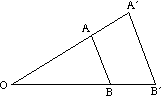
![]()
![]()
拡大の性質
三角形PQRは、中心Oを持つ拡大の下の三角形PQRに写像する。
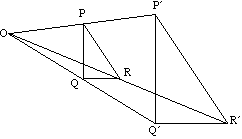
線とその画像は常に平行です。例えば、PqはPq
と平行である角度サイズは不変である。例えば、![]() PQR=
PQR=![]() PQR
PQR
拡大の中心が唯一の不変点です。
長さと面積は、m=1または−1の場合を除いて不変ではありません。
つまり、拡大は等長ではありません。
拡大は直接変換です。
すなわち、
PQRと
PQRは両方とも反時計回りです。
λが長さのスケール係数の場合、m μ2は面積のスケール係数です。
異なるスケールファクタ
以下の図は、中心Oを中心とする三角形ABCの拡大に及ぼすさまざまなスケールファクタの影響を示しています。
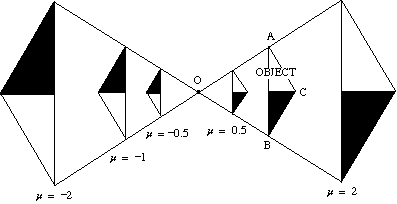
- スケール係数が正の場合、オブジェクトとイメージの両方が中心の同じ側にあります。
- スケール係数が負の場合、オブジェクトと画像は中心の反対側にあります。
画像は反転しています。
拡大の例を参照してください− ![]()
拡大の中心の位置
図とその画像が与えられた場合、拡大の中心を見つけるには:
1。 ポイントとその画像を結合します。
2. 別の点とその画像について繰り返します。
3. 拡大の中心は、これらの線の交点です。
同様の図形
図形は同じ形状であれば類似しています。
- 同様の図形は、拡大によって、または反射、回転、平行移動と拡大の組み合わせによって互いにマッピングすることができます。
- 同様の図形の対応する角度は等しい。
- 対応する辺は互いに比例します。
型1
![]() YXZは、対応する角度が等しいため、
YXZは、対応する角度が等しいため、![]() PQMに似ています。
PQMに似ています。
|
|
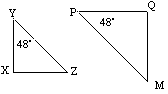 |
![]() YXZは、変換の組み合わせによって
YXZは、変換の組み合わせによって![]() PQMにマッピングできます。
PQMにマッピングできます。
スケール係数=µ= ![]()
タイプ2
![]() ABCは
ABCは![]() ADEに似ています。:
ADEに似ています。:
|
(DEはBCと平行です) |
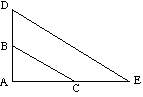 |
![]() ABCは拡大によって
ABCは拡大によって![]() ADEにマッピングすることができます。
ADEにマッピングすることができます。
スケール係数=µ= ![]()
|
(a)(i)二つの三角形AとBは類似しています。 Pとqを見つける。 |
(a)(i)a p= 2 × 10 p=20 2x q=12 q= 6 |
|
(ii)三角形Aの面積は24単位です2。 |
(ii)面積のスケール係数=μ2=4 三角形Bの面積=4x三角形Aの面積=4×24=96units2 |
|
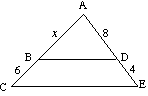
(B)BDがCEに平行である場合、xを見つける |
(B)
12x=8(x+6) 12x=8x+48 4x=48 x= 12 |
反射、回転、翻訳、拡大を示すインタラクティブなスプレッドシート(Microsoft Excel)をダウンロードします。
![]()
(Windowsユーザーは、右クリックして「ターゲットを名前を付けて保存します。..”お使いのコンピュータ上のファイルを保存します。)