Derivati di ordine superiore

Ultimo aggiornamento il 31 luglio 2021

I derivati di ordine superiore possono acquisire informazioni su una funzione che i derivati di primo ordine da soli non possono acquisire.

Le derivate del Primo ordine possono acquisire informazioni importanti, come il tasso di variazione, ma da sole non possono distinguere tra minimi o massimi locali, dove il tasso di variazione è zero per entrambi. Diversi algoritmi di ottimizzazione affrontano questa limitazione sfruttando l’uso di derivate di ordine superiore, come nel metodo di Newton in cui le derivate del secondo ordine vengono utilizzate per raggiungere il minimo locale di una funzione di ottimizzazione.

In questo tutorial, scoprirai come calcolare le derivate univariate e multivariate di ordine superiore.

Dopo aver completato questo tutorial, saprai:

• Come calcolare le derivate di ordine superiore delle funzioni univariate.
• Come calcolare le derivate di ordine superiore delle funzioni multivariate.
• Come le derivate del secondo ordine possono essere sfruttate nell’apprendimento automatico da algoritmi di ottimizzazione del secondo ordine.

Iniziamo.

Panoramica del tutorial

Questo tutorial è diviso in tre parti; sono:

• di Ordine Superiore Derivati di Univariata Funzioni
• di Ordine Superiore derivate di Funzioni Multivariate
• Applicazione di Apprendimento automatico

di Ordine Superiore Derivati di Univariata Funzioni

In aggiunta al primo ordine derivati, che abbiamo visto ci può fornire importanti informazioni su una funzione, come il tasso istantaneo di variazione, di ordine superiore derivati possono anche essere altrettanto utile. Ad esempio, la derivata seconda può misurare l’accelerazione di un oggetto in movimento o può aiutare un algoritmo di ottimizzazione a distinguere tra un massimo locale e un minimo locale.

Calcolare derivate di ordine superiore (secondo, terzo o superiore) di funzioni univariate non è così difficile.

La derivata seconda di una funzione è solo la derivata della sua derivata prima. Il terzo derivato è il derivato del secondo derivato, il quarto derivato è il derivato del terzo e così via.

Quindi, calcolare le derivate di ordine superiore comporta semplicemente differenziare ripetutamente la funzione. Per farlo, possiamo semplicemente applicare la nostra conoscenza della regola del potere. Consideriamo la funzione, f (x) = x3 + 2×2 – 4x + 1, come esempio. Quindi:

Prima derivata: f'(x) = 3×2 + 4x-4

Seconda derivata: f”(x) = 6x + 4

Terza derivata: f”‘(x) = 6

Quarta derivata: f (4)(x) = 0

Quinta derivata: f (5)(x) = 0 ecc.

Quello che abbiamo fatto qui è che abbiamo prima applicato la regola di potenza a f (x) per ottenere la sua prima derivata, f'(x), quindi applicato la regola di potenza alla prima derivata per ottenere la seconda, e così via. La derivata, alla fine, andrà a zero mentre la differenziazione viene applicata ripetutamente.

L’applicazione delle regole del prodotto e del quoziente rimane valida anche per ottenere derivati di ordine superiore, ma il loro calcolo può diventare sempre più disordinato all’aumentare dell’ordine. La regola generale di Leibniz semplifica il compito in questo aspetto, generalizzando la regola del prodotto per:

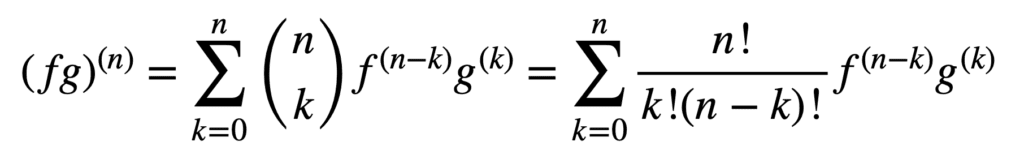
Qui, il termine, n! / k!(n-k)!, è il coefficiente binomiale dal teorema binomiale, mentre f (k) e g(k) denotano la derivata kth delle funzioni, f e g, rispettivamente.

Pertanto, trovando la prima e la seconda derivata (e, quindi, sostituendo n = 1 e n = 2, rispettivamente), dalla regola generale di Leibniz, ci dà:

(fg)(1) = (fg)’ = f (1) g + f g(1)

(fg)(2) = (fg)” = f (2) g + 2f (1) g(1) + f g(2)

Notare la derivata prima familiare come definita dalla regola del prodotto. La regola di Leibniz può anche essere usata per trovare derivate di ordine superiore di funzioni razionali, poiché il quoziente può essere efficacemente espresso in un prodotto della forma, f g-1.

Derivate di ordine superiore di funzioni multivariate

La definizione di derivate parziali di ordine superiore di funzioni multivariate è analoga al caso univariato: la derivata parziale dell’n ° ordine per n > 1, viene calcolata come derivata parziale della derivata parziale dell’ordine (n – 1). Ad esempio, prendendo la seconda derivata parziale di una funzione con due variabili si ottengono quattro derivate parziali seconde: due derivate parziali proprie, fxx e fyy e due derivate parziali incrociate, fxy e fyx.

Per prendere una “derivata”, dobbiamo prendere una derivata parziale rispetto a x o y, e ci sono quattro modi per farlo: x poi x, x poi y, y poi x, y poi y.

– Pagina 371, Calcolo singolo e multivariabile, 2020.

Consideriamo la funzione multivariata, f(x, y) = x2 + 3xy + 4y2, per la quale vorremmo trovare le seconde derivate parziali. Il processo inizia con la ricerca delle sue derivate parziali del primo ordine, prima: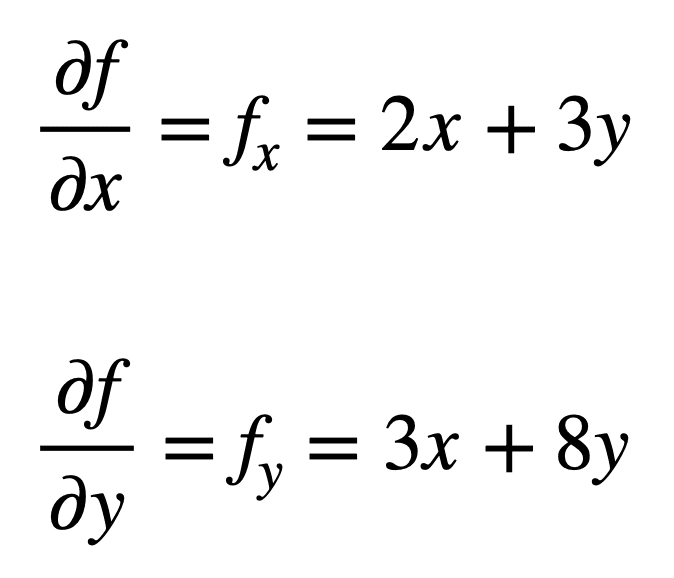

Le quattro derivate parziali del secondo ordine vengono poi trovate ripetendo il processo di ricerca delle derivate parziali, delle derivate parziali. Le proprie derivate parziali sono le più semplici da trovare, poiché ripetiamo semplicemente il processo di differenziazione parziale, rispetto a x o y, una seconda volta:

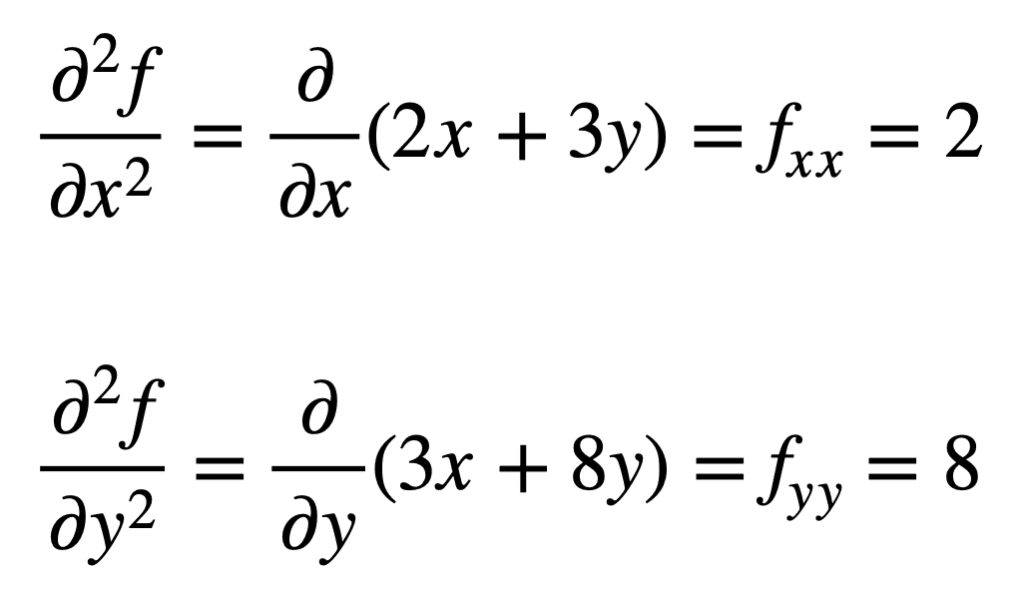
La derivata parziale incrociata dell’fx precedentemente trovato (cioè la derivata parziale rispetto a x) si trova prendendo la derivata parziale del risultato rispetto a y, dandoci fxy. Allo stesso modo, prendendo la derivata parziale di fy rispetto a x, ci dà fyx:

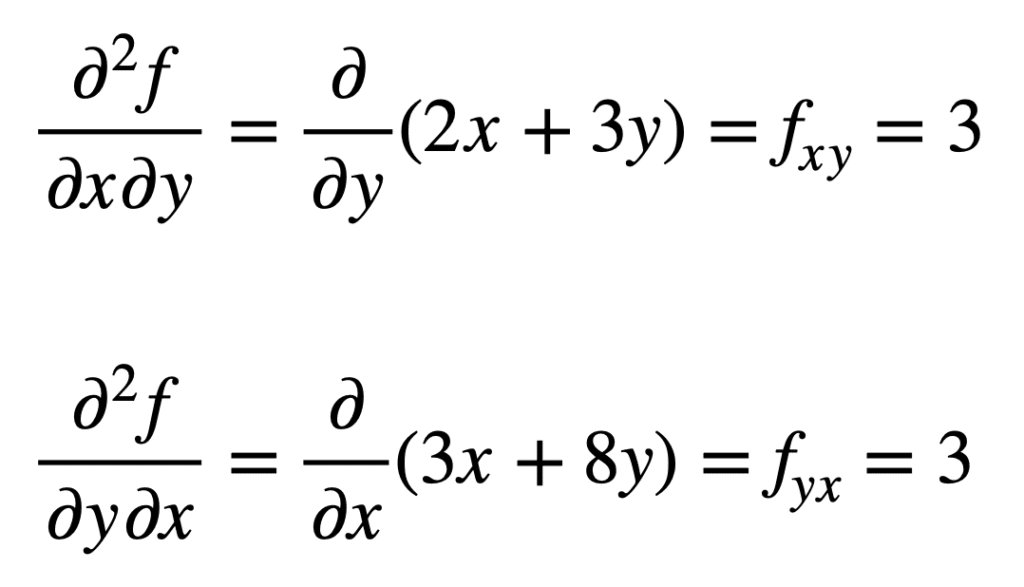
Non è un caso che le derivate parziali incrociate diano lo stesso risultato. Questo è definito dal teorema di Clairaut, che afferma che finché le derivate parziali incrociate sono continue, allora sono uguali.

Applicazione nell’apprendimento automatico

Nell’apprendimento automatico, è la derivata del secondo ordine che viene utilizzata principalmente. Avevamo già detto che la derivata seconda può fornirci informazioni che la derivata prima da sola non può acquisire. In particolare, può dirci se un punto critico è un minimo o un massimo locale (in base al fatto che la derivata seconda sia maggiore o minore di zero, rispettivamente), per cui la derivata prima sarebbe, altrimenti, zero in entrambi i casi.

Esistono diversi algoritmi di ottimizzazione del secondo ordine che sfruttano queste informazioni, uno dei quali è il metodo di Newton.

Le informazioni del secondo ordine, d’altra parte, ci permettono di fare un’approssimazione quadratica della funzione obiettivo e approssimare la giusta dimensione del passo per raggiungere un minimo locale

-Page 87, Algorithms for Optimization, 2019.

Nel caso univariato, il metodo di Newton utilizza un’espansione della serie di Taylor del secondo ordine per eseguire l’approssimazione quadratica attorno a un punto della funzione obiettivo. La regola di aggiornamento per il metodo di Newton, che si ottiene impostando la derivata su zero e risolvendo per la radice, comporta un’operazione di divisione per la derivata seconda. Se il metodo di Newton viene esteso all’ottimizzazione multivariata, la derivata viene sostituita dal gradiente, mentre il reciproco della derivata seconda viene sostituito con l’inverso della matrice di Iuta.

Tratteremo le approssimazioni delle serie di Iuta e Taylor, che sfruttano l’uso di derivati di ordine superiore, in tutorial separati.

Ulteriori letture

Questa sezione fornisce più risorse sull’argomento se stai cercando di approfondire.

Libri

• Calcolo singolo e multivariabile, 2020.
• Calcolo per manichini, 2016.
• Apprendimento profondo, 2017.
• Algoritmi per l’ottimizzazione, 2019.

Riepilogo

In questo tutorial, hai scoperto come calcolare le derivate univariate e multivariate di ordine superiore.

In particolare, hai imparato:

• Come calcolare le derivate di ordine superiore delle funzioni univariate.
• Come calcolare le derivate di ordine superiore delle funzioni multivariate.
• Come le derivate del secondo ordine possono essere sfruttate nell’apprendimento automatico da algoritmi di ottimizzazione del secondo ordine.