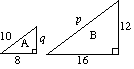Un ingrandimento è una trasformazione in cui un oggetto viene mappato a un’immagine della stessa forma ma di dimensioni diverse. Si dice che l’oggetto e l’immagine siano simili. Un allargamento richiede un centro di allargamento e un fattore di scala.
la Notazione
E è un allargamento, con il centro di ampliamento O e fattore di scala µ.
E: AB 
AB
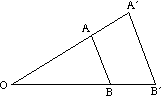
Proprietà dell’ingrandimento
Triangolo PQR mappa al triangolo PQR sotto ingrandimento con centro O.
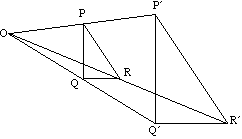
Le linee e le loro immagini sono sempre parallele.
ad esempio PQ è parallelo a PQ
La dimensione dell’angolo è invariante.
ad esempio
PQR =
Il centro dell’allargamento è l’unico punto invariante.
Lunghezza e area non sono invarianti, tranne quando m = 1 o-1.
cioè l’allargamento non è un’isometria.
L’allargamento è una trasformazione diretta.
cioè
PQR e
Se μ è il fattore di scala per la lunghezza, mµ 2 è il fattore di scala per l’area.
Diversi Fattori di Scala
Il diagramma qui sotto mostra l’effetto di una varietà di fattori di scala sull’allargamento di un triangolo ABC su centro O.
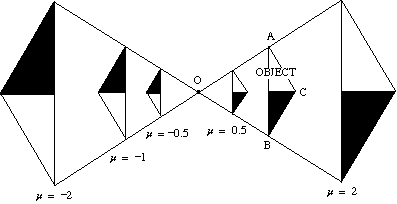
- Se il fattore di scala è positivo, sia per l’oggetto e l’immagine sono sullo stesso lato del centro.
- Se il fattore di scala è negativo, l’oggetto e l’immagine si trovano ai lati opposti del centro.
L’immagine è invertita.
Vedi esempi di allargamenti− 
Posizione del Centro dell’allargamento
Data una figura e la sua immagine, per trovare il centro dell’allargamento:
1. Unire un punto e la sua immagine.
2. Ripeti per un altro punto e la sua immagine.
3. Il centro dell’allargamento è l’intersezione di queste linee.
Figure simili
Le figure sono simili se hanno la stessa forma.
- Cifre simili possono essere mappate l’una sull’altra mediante un allargamento o una combinazione di riflessione, rotazione o traslazione e un allargamento.
- Gli angoli corrispondenti di figure simili sono uguali.
- I lati corrispondenti sono proporzionali tra loro.
Tipo 1
YXZ è simile a PQM in quanto hanno angoli corrispondenti uguali.
|
|
 |
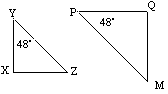YXZ può essere mappato a PQM da una combinazione di trasformazioni.
Fattore di scala = µ = 
Tipo 2
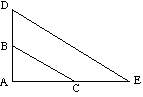
ABC è simile a ADE perché:
|
(DE è parallelo a BC) |
 |
ABC può essere mappato su ADE da un allargamento.
fattore di Scala = µ = 
|
(a) (i) I due triangoli A e B sono simili. Trova p e q. |
(a) i) Per A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) L’area del triangolo A è di 24 unità2. |
(ii) fattore di Scala per area = µ2 = 4 Area del triangolo B = 4 x area di Un triangolo |
|
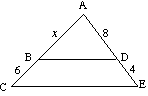
(b) Trovare la x, se BD è parallelo al CE |
(b) Per
  12x = 8(x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B , fattore di scala = 2 
ABD
Scarica interattiva di foglio di calcolo (Microsoft Excel), mostrando riflessioni, rotazioni, le traduzioni e gli ampliamenti.
(Utenti Windows, fare clic destro e ” Salva destinazione con nome…”per salvare i file sul tuo computer.)
