Utoljára frissítve: július 31, 2021
a magasabb rendű származékok információkat gyűjthetnek egy olyan funkcióról, amelyet az elsőrendű származékok önmagukban nem tudnak rögzíteni.
az elsőrendű származékok fontos információkat rögzíthetnek, például a változás sebességét, de önmagukban nem tudnak különbséget tenni a helyi minimumok vagy maximumok között, ahol a változás sebessége nulla mindkettőnél. Számos optimalizálási algoritmus foglalkozik ezzel a korlátozással a magasabb rendű származékok használatának kihasználásával, például Newton módszerében, ahol a másodrendű származékokat használják az optimalizálási függvény helyi minimumának elérésére.
ebben az oktatóanyagban megtudhatja, hogyan kell kiszámítani a magasabb rendű egyváltozós és többváltozós származékokat.
miután befejezte ezt az oktatóanyagot, tudni fogja:
- az egyváltozós függvények magasabb rendű deriváltjainak kiszámítása.
- hogyan számítsuk ki a többváltozós függvények magasabb rendű deriváltjait.
- hogyan lehet A másodrendű származékokat kihasználni a gépi tanulásban másodrendű optimalizálási algoritmusokkal.
kezdjük.

magasabb rendű származékok
fotó: Jairph, néhány jog fenntartva.
bemutató Áttekintés
ez a bemutató három részre oszlik; ezek:
- egyváltozós függvények magasabb rendű származékai
- többváltozós függvények magasabb rendű származékai
- alkalmazás a gépi tanulásban
egyváltozós függvények magasabb rendű származékai
az elsőrendű származékokon kívül, amelyeket láttunk, fontos információkat szolgáltathat nekünk egy függvényről, például annak pillanatnyi változási sebessége, a magasabb rendű származékok is ugyanolyan hasznosak lehetnek. Például a második derivált egy mozgó objektum gyorsulását mérheti, vagy segíthet egy optimalizálási algoritmusnak megkülönböztetni a helyi maximumot és a helyi minimumot.
az egyváltozós függvények magasabb rendű (második, harmadik vagy magasabb) származékainak kiszámítása nem olyan nehéz.
egy függvény második deriváltja csak az első deriváltjának deriváltja. A harmadik származék a második származék származéka, a negyedik származék a harmadik származéka stb.
ezért a magasabb rendű származékok kiszámítása egyszerűen magában foglalja a függvény ismételt megkülönböztetését. Ennek érdekében egyszerűen alkalmazhatjuk a hatalmi szabály ismereteit. Vegyük példaként az f(x) = x3 + 2×2 – 4x + 1 függvényt. Ezután:
első származék: f'(x) = 3×2 + 4x – 4
második származék: f”(x) = 6x + 4
harmadik származék: f”‘(x) = 6
negyedik származék: f (4)(x) = 0
ötödik származék: f (5)(x) = 0 stb.
amit itt tettünk, az az, hogy először alkalmaztuk a hatványszabályt f(x) – re, hogy megkapjuk az első deriváltját, f'(x), majd alkalmaztuk a hatványszabályt az első deriváltra a második megszerzése érdekében stb. A derivált végül nulla lesz, mivel a differenciálást ismételten alkalmazzák.
a termék-és hányadosszabályok alkalmazása továbbra is érvényes a magasabb rendű derivatívák megszerzésére, de számításuk a sorrend növekedésével egyre rendetlenebbé válhat. Az Általános Leibniz-szabály leegyszerűsíti a feladatot ebben a vonatkozásban, a termékszabály általánosításával:
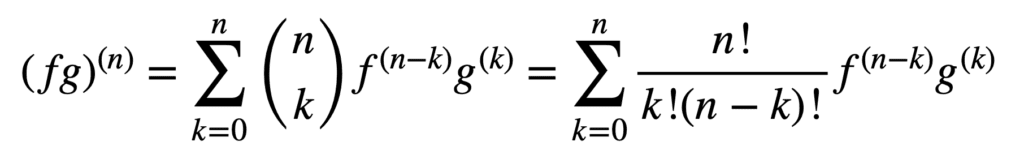
itt a kifejezés, n! k!(n-k)!, a binomiális tétel binomiális együtthatója, míg f (k) és g(k) a függvények k-dik deriváltját jelöli, F és g, ill.
ezért az első és a második derivált megtalálása (és ezáltal N = 1 és n = 2 helyettesítése) az Általános Leibniz-szabály szerint:
(fg) (1) = (fg) ‘ = f (1 ) g + f g(1)
(fg)(2) = (fg)” = f (2) g + 2F (1) g(1) + f g(2)
vegye figyelembe a termékszabályban meghatározott ismerős első származékot. A Leibniz-szabály felhasználható a racionális függvények magasabb rendű deriváltjainak megtalálására is, mivel a hányados hatékonyan kifejezhető a forma termékévé, f g-1.
többváltozós függvények magasabb rendű Deriváltjai
a többváltozós függvények magasabb rendű parciális deriváltjainak meghatározása Analóg az egyváltozós esettel: az n-edik rendű parciális derivált n > 1 esetén az (n – 1)rendű parciális derivált parciális deriváltjaként kerül kiszámításra. Például, ha egy függvény második parciális deriváltját két változóval vesszük, akkor négy, második parciális derivált jön létre: két saját parciális derivált, fxx és fyy, valamint két kereszt parciális derivált, fxy és fyx.
ahhoz, hogy “deriváltat” vegyünk, részleges deriváltat kell vennünk x vagy y vonatkozásában, és négyféleképpen lehet megtenni: x majd x, x majd y, y majd x, y majd y.
– 371.oldal, egy-és többváltozós számítás, 2020.
tekintsük a többváltozós függvényt, f(x, y) = x2 + 3XY + 4y2, amelyhez szeretnénk megtalálni a második részleges származékokat. A folyamat az elsőrendű parciális deriváltjainak megtalálásával kezdődik, első: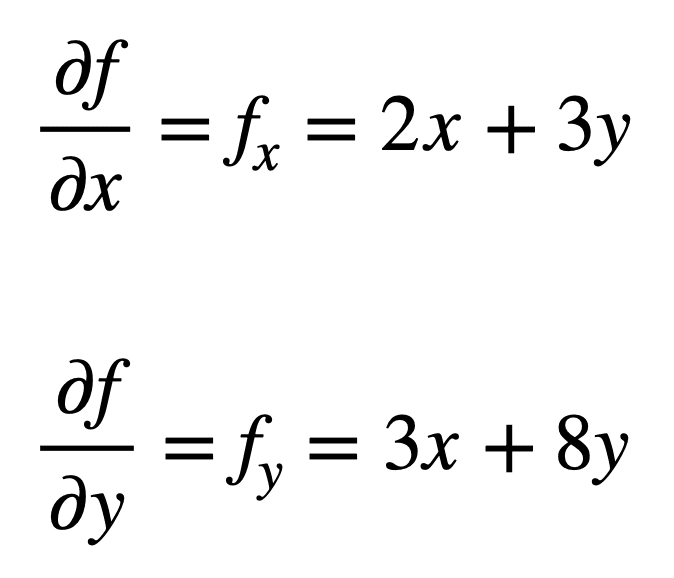
a négy, másodrendű parciális származékot ezután úgy találjuk meg, hogy megismételjük a parciális származékok, a parciális származékok megtalálásának folyamatát. A saját parciális deriváltakat lehet A legegyszerűbben megtalálni, mivel egyszerűen megismételjük a részleges differenciálódási folyamatot X vagy y vonatkozásában másodszor:
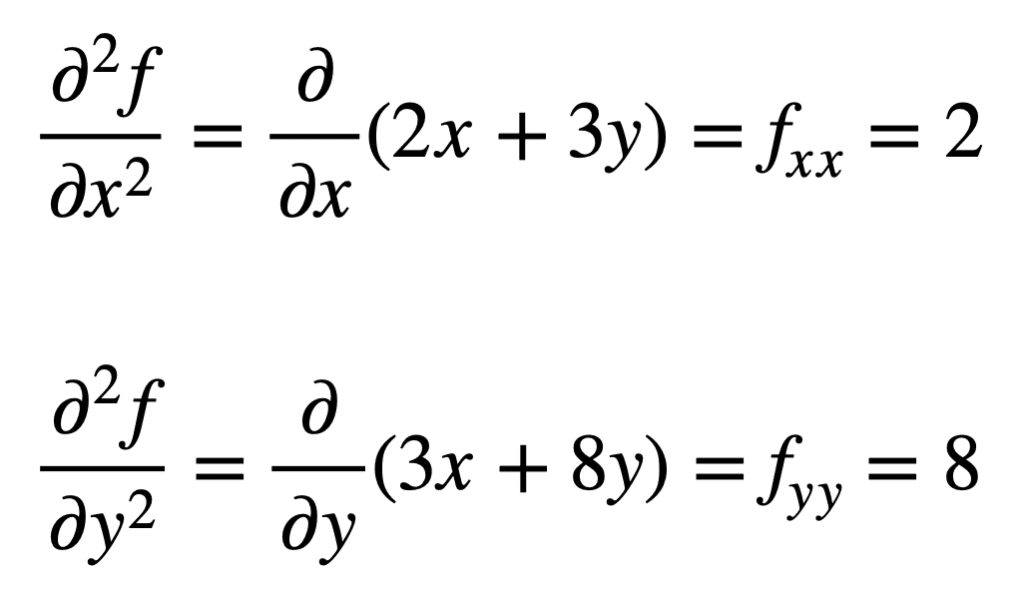
a korábban talált FX kereszt-parciális deriváltját (vagyis az X-hez viszonyított parciális deriváltot) úgy találjuk meg, hogy az eredmény részleges deriváltját vesszük az y-hez viszonyítva, így fxy-t kapunk. Hasonlóképpen, figyelembe véve a részleges derivált nak, – nek fy x, ad nekünk fyx:
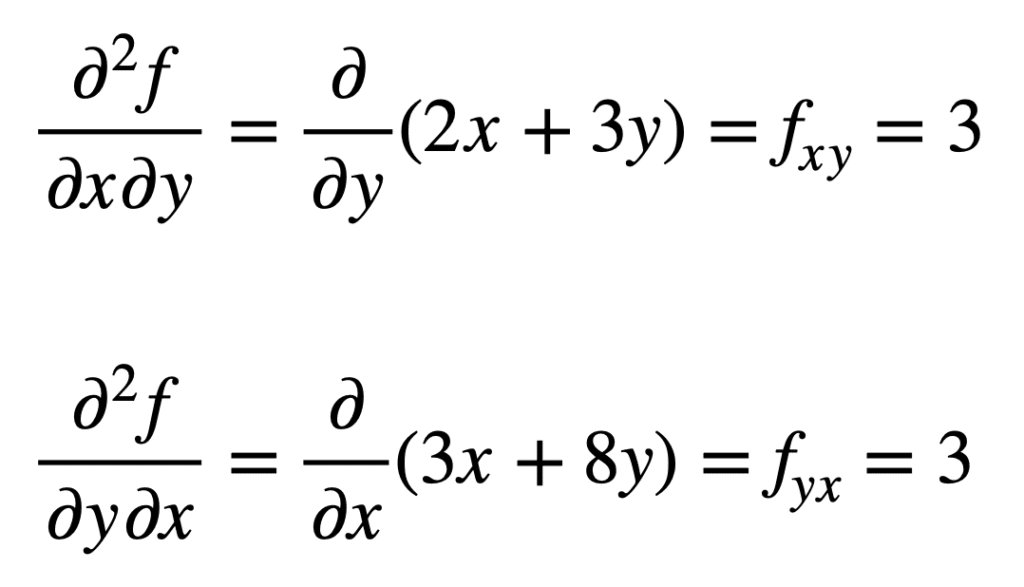
nem véletlen, hogy a kereszt-parciális származékok ugyanazt az eredményt adják. Ezt Clairaut tétele határozza meg, amely kimondja, hogy mindaddig, amíg a kereszt parciális deriváltak folyamatosak, akkor egyenlőek.
alkalmazás a gépi tanulásban
a gépi tanulásban ez a másodrendű származék, amelyet leginkább használnak. Korábban említettük, hogy a második derivált olyan információkat szolgáltathat nekünk, amelyeket az első derivált önmagában nem képes megragadni. Pontosabban meg tudja mondani, hogy egy kritikus pont lokális minimum vagy maximum (annak alapján, hogy a második derivált nagyobb vagy kisebb, mint nulla), amelyre az első derivált egyébként mindkét esetben nulla lenne.
számos másodrendű optimalizálási algoritmus létezik, amelyek kihasználják ezt az információt, amelyek közül az egyik a Newton-módszer.
a másodrendű információk viszont lehetővé teszik a célfüggvény másodfokú közelítését és a megfelelő lépésméret közelítését a helyi minimum eléréséhez …
-87.oldal, algoritmusok az optimalizáláshoz, 2019.
az egyváltozós esetben Newton módszere másodrendű Taylor-sorozatbővítést használ a másodfokú közelítés végrehajtására a célfüggvény egy bizonyos pontja körül. A Newton-módszer frissítési szabálya, amelyet úgy kapunk, hogy a deriváltat nullára állítjuk, és a gyökérre megoldjuk, magában foglalja a második derivált osztási műveletét. Ha Newton módszerét kiterjesztjük a többváltozós optimalizálásra, akkor a derivált helyébe a gradiens lép, míg a második derivált reciprokját a hesseni mátrix inverzével helyettesítjük.
mi lesz, amely a Hessian és Taylor sorozat közelítések, amelyek kihasználják a használatát magasabb rendű származékok, külön útmutatók.
további olvasmányok
ez a szakasz további forrásokat tartalmaz a témában, ha mélyebbre szeretne menni.
Könyvek
- egy-és többváltozós kalkulus, 2020.
- kalkulus kezdőknek, 2016.
- Mély Tanulás, 2017.
- algoritmusok az optimalizáláshoz, 2019.
összefoglaló
ebben az oktatóanyagban felfedezted, hogyan kell kiszámítani a magasabb rendű egyváltozós és többváltozós származékokat.
konkrétan megtanultad:
- az egyváltozós függvények magasabb rendű deriváltjainak kiszámítása.
- hogyan számítsuk ki a többváltozós függvények magasabb rendű deriváltjait.
- hogyan lehet A másodrendű származékokat kihasználni a gépi tanulásban másodrendű optimalizálási algoritmusokkal.
