ez a példa az FBI 2006-os bűnügyi statisztikáin alapul. Különösen érdekel minket az állam mérete és a városban elkövetett gyilkosságok száma közötti kapcsolat.
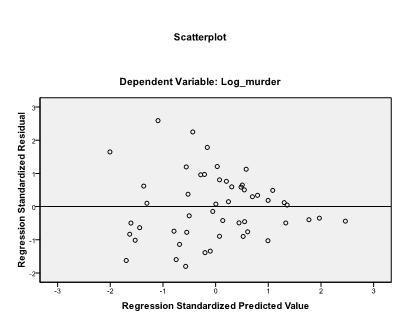
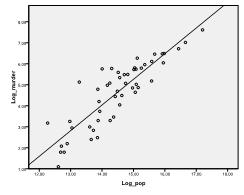
először ellenőriznünk kell, hogy van-e lineáris kapcsolat az adatokban. Ehhez ellenőrizzük a szórást. A szórási diagram jó lineáris kapcsolatot jelez, amely lehetővé teszi lineáris regressziós elemzés elvégzését. Ellenőrizhetjük a Pearson kétváltozós korrelációját is, és megállapíthatjuk, hogy mindkét változó erősen korrelál (r = .959, p < 0,001).

fedezze fel, hogyan segítünk szerkeszteni a dolgozat fejezeteit
az elméleti keret összehangolása, cikkek összegyűjtése, hiányosságok szintetizálása, világos módszertan és adatterv megfogalmazása, valamint a kutatás elméleti és gyakorlati következményeinek írása átfogó disszertációszerkesztő szolgáltatásaink részét képezik.
- hozd értekezés szerkesztési szakértelem fejezetek 1-5 időben.
- Kövesse nyomon az összes változást, majd dolgozzon veled, hogy tudományos írást hozzon létre.
- folyamatos támogatás a Bizottság visszajelzéseinek kezelésére, a felülvizsgálatok csökkentésére.
másodszor, ellenőriznünk kell a többváltozós normalitást. Példánkban azt találjuk, hogy a többváltozós normalitás nem biztos, hogy jelen van.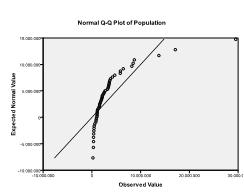
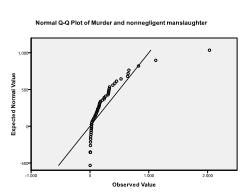
a Kolmogorov-Szmirnov teszt megerősíti ezt a gyanút (p = 0,002 és p = 0.006). Az ln-transzformáció elvégzése a két változón megoldja a problémát és létrehozza a többváltozós normalitást (K-S teszt p = .991 és p = .543).
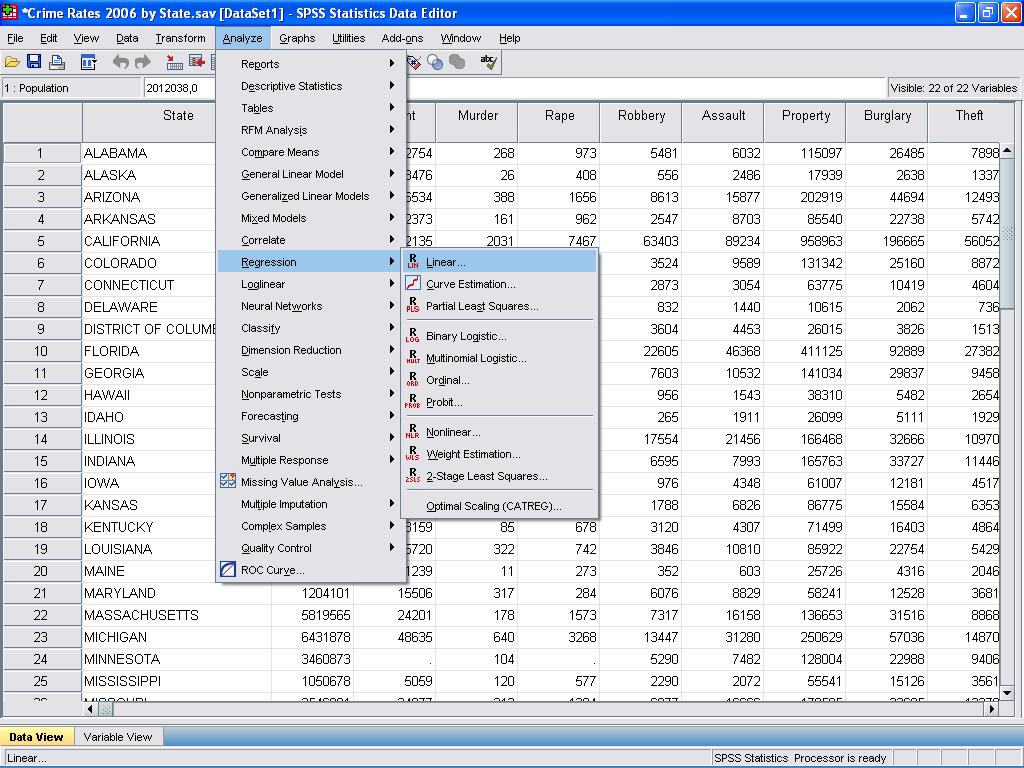
most elvégezhetjük a lineáris regresszióanalízist. Lineáris regresszió található SPSS ban ben elemzés / regresszió / lineáris…
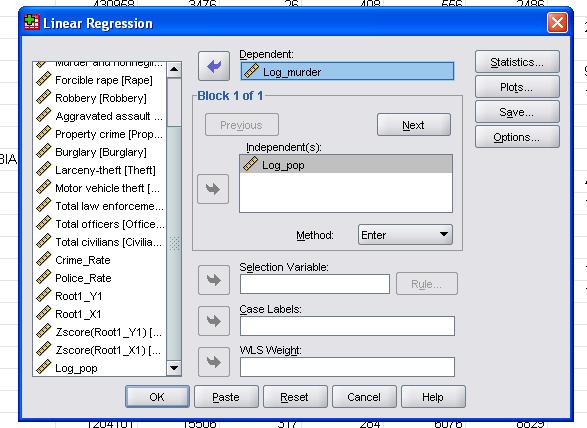
ebben az egyszerű esetben csak a log_pop és log_murder változókat kell hozzáadnunk a modellhez függő és független változókként.
a terepi statisztikák lehetővé teszik számunkra, hogy további statisztikákat tartalmazzunk, amelyekre szükségünk van a lineáris regressziós elemzés érvényességének értékeléséhez.
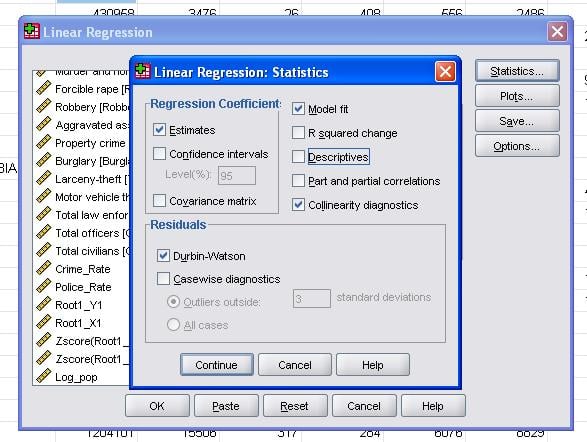
ajánlatos kiegészíteni a kollinearitás diagnosztikát és a Durbin-Watson tesztet az auto-korrelációhoz. A maradványok homoszkedaszticitásának feltételezésének teszteléséhez egy speciális telket is belefoglalunk a parcellák menübe.
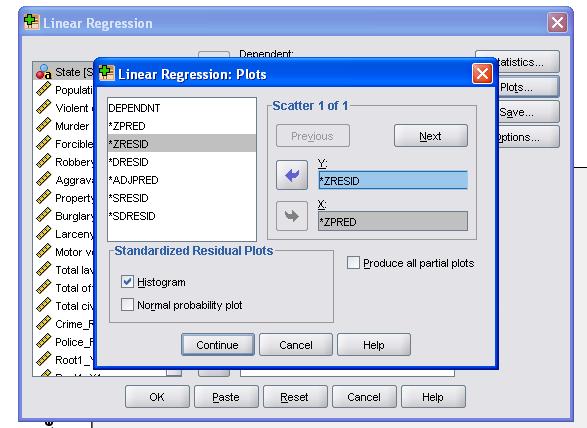
a lineáris regresszióanalízis SPSS szintaxisa
regresszió
/ hiányzó LISTWISE
/ statisztika COEFF out R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) tőkehal(.10)
/NOORIGIN
/függő Log_murder
/módszer=adja meg a Log_pop
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/maradványok DURBIN HIST(ZRESID).
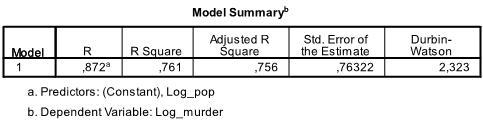
a kimenet első táblázata a modellösszefoglalót és az Általános illesztési statisztikákat mutatja. Megállapítottuk, hogy modellünk korrigált R2 értéke 0,756 az R2 = értékkel .761 ez azt jelenti, hogy a lineáris regresszió megmagyarázza a 76-ot.Az adatok varianciájának 1% – a. A Durbin-Watson d = 2,323, amely a két kritikus érték között van 1,5 < d < 2,5, ezért feltételezhetjük, hogy az adatokban nincs elsőrendű lineáris automatikus korreláció.
a következő táblázat az F-teszt, a lineáris regresszió F-tesztjének nullhipotézise, hogy nincs lineáris kapcsolat a két változó között (más szóval R2=0). F = 156.2 és 50 szabadságfok a teszt igen jelentős, így feltételezhetjük, hogy lineáris összefüggés van a modellünkben szereplő változók között.


a következő táblázat a regressziós együtthatókat, az elfogást és az összes együttható és az elfogás jelentőségét mutatja a modellben. Megállapítottuk, hogy lineáris regressziós elemzésünk a lineáris regressziós függvényt y = -13.067 + 1.222
* x. Felhívjuk figyelmét, hogy ez nem fordítja le van 1.2 további gyilkosság minden 1000 további lakosra, mert átalakítottuk a változókat.
ha újra futtatjuk a lineáris regresszióanalízist az eredeti változókkal, akkor y = 11.85 + 6.7*10-5 ami azt mutatja, hogy minden 10,000 további lakosra 6,7 további gyilkosságot várnánk.
lineáris regressziós analízisünkben a teszt azt a nullhipotézist teszteli, hogy az együttható 0. A t-teszt megállapítja, hogy mind az elfogó, mind a változó nagyon szignifikáns (p < 0,001), ezért azt mondhatjuk, hogy különböznek a nullától.

ez a táblázat tartalmazza a béta súlyokat is (amelyek a független változók relatív fontosságát fejezik ki) és a kollinearitási statisztikákat. Mivel azonban elemzésünkben csak 1 független változó van, nem figyelünk ezekre az értékekre.
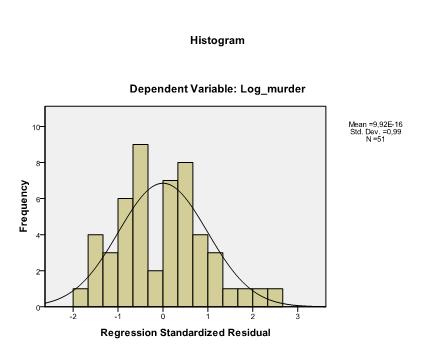
az utolsó dolog, amit ellenőriznünk kell, a maradványok homoszkedaszticitása és normalitása. A hisztogram azt jelzi, hogy a maradványok megközelítik a normális eloszlást. A Z*pred és z*presid Q-Q-diagramja azt mutatja, hogy lineáris regressziós analízisünkben nincs tendencia a hibakifejezésekben.