tämä esimerkki perustuu FBI: n vuoden 2006 rikostilastoihin. Meitä kiinnostaa erityisesti valtion koon ja kaupungissa tehtyjen murhien määrän suhde.
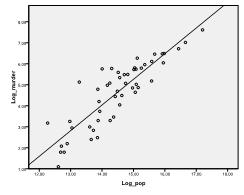
ensin on tarkistettava, onko aineistossa lineaarista suhdetta. Sitä varten tarkistamme scatterplotin. Scatter-käyrä osoittaa hyvän lineaarisen suhteen, jonka avulla voimme tehdä lineaarisen regressioanalyysin. Voimme myös tarkistaa Pearsonin Bivariate-korrelaation ja todeta, että molemmat muuttujat ovat hyvin korreloituneita (r = .959, P < 0, 001).

tutustu siihen, miten autamme muokkaamaan Väitöskirjasi lukuja
yhtenäistämällä teoreettista viitekehystä, keräämällä artikkeleita, syntetisoimalla aukkoja, artikuloimalla selkeää metodologiaa ja datasuunnitelmaa sekä kirjoittamalla tutkimuksesi teoreettisista ja käytännön vaikutuksista ovat osa kattavia väitöskirjan editointipalvelujamme.
- tuo väitöskirjan editointiosaaminen lukuihin 1-5 ajoissa.
- seuraa kaikki muutokset ja työskentele sitten kanssasi tieteellisen kirjoittamisen aikaansaamiseksi.
- jatkuva tuki valiokuntapalautteen käsittelylle, mikä vähentää tarkistuksia.
toiseksi meidän on tarkistettava monimuuttujanormaalisuus. Esimerkissämme huomaamme, että monimuuttujainen normaalius ei välttämättä ole läsnä.
Kolmogorov-Smirnovin testi vahvistaa tämän epäilyn (P = 0, 002 ja p = 0.006). Ln-muunnoksen tekeminen kahdelle muuttujalle korjaa ongelman ja muodostaa monimuuttujanormaalisuuden (K-s-testi p = .991 ja p = .543).
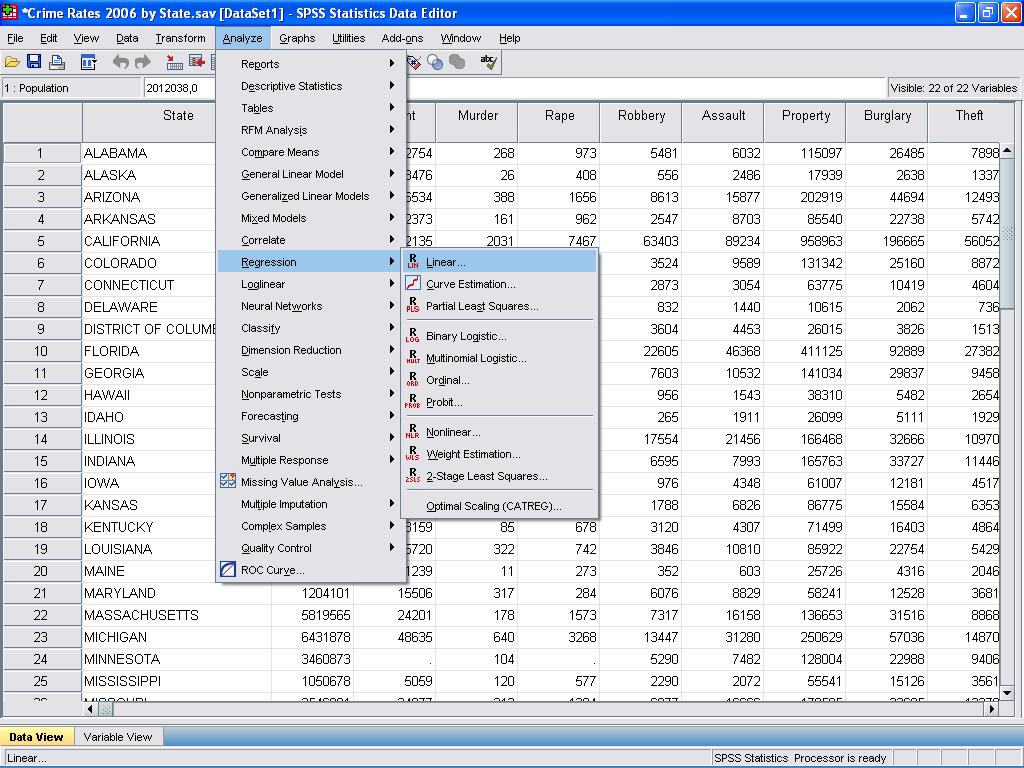
voimme tehdä lineaarisen regressioanalyysin. Lineaarinen regressio löytyy SPSS: stä Analysis / regressio / Lineaarinen…
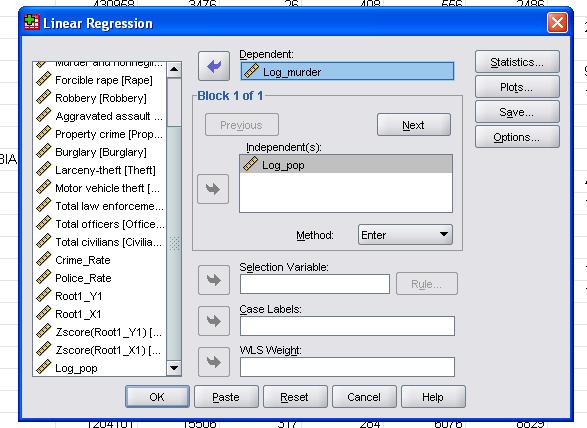
tässä yksinkertaisessa tapauksessa on vain lisättävä muuttujat log_pop ja log_murder malliin riippuvaisiksi ja itsenäisiksi muuttujiksi.
kenttätilastojen avulla voimme lisätä lisää tilastoja, joita tarvitsemme lineaarisen regressioanalyysin pätevyyden arvioimiseksi.
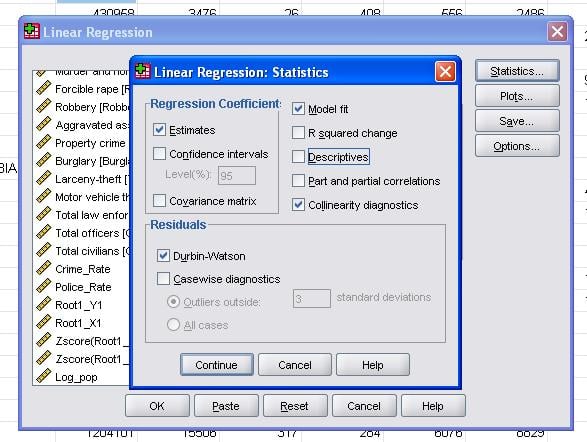
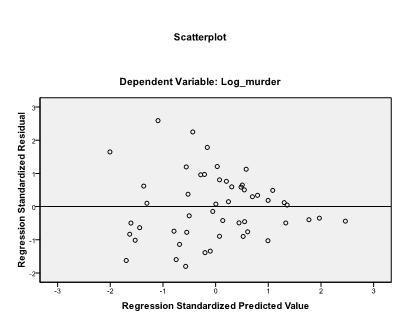
on suositeltavaa sisällyttää lisäksi kollineaarisuusdiagnostiikka ja Durbin-Watson-testi autokorrelaation määrittämiseksi. Testaamaan oletus homoscedasticity residuals olemme myös erityisen tontin tontteja valikosta.
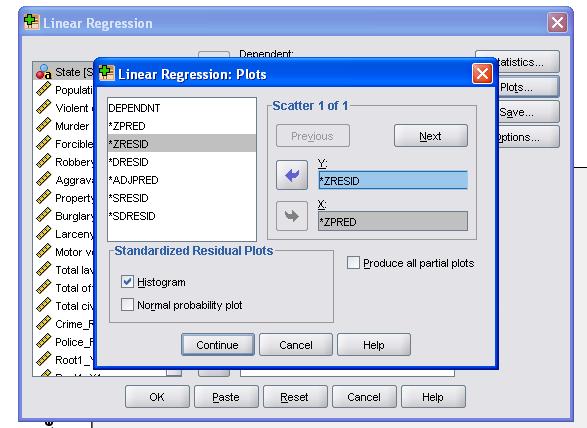
SPSS: n syntaksi lineaarisessa regressioanalyysissä on
regressio
/puuttuva LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) Pouta(.10)
/NOORIGIN
/DEPENDENT Log_murder
/METHOD=ENTER Log_pop
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS DURBIN HIST(ZRESID).
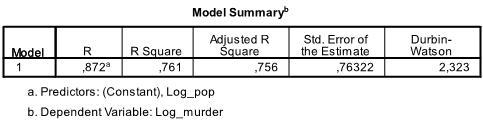
lähdön ensimmäisessä taulukossa on malliyhteenveto ja yleiskuntotilastot. Havaitsemme, että mallimme mukautettu R2 on 0,756 R2=: n kanssa .761 eli lineaarinen regressio selittää 76.1% tietojen varianssista. Durbin-Watson d = 2,323, joka on kahden kriittisen arvon 1,5 < d < 2,5 välissä, joten voimme olettaa, ettei aineistossa ole ensimmäisen kertaluvun lineaarista autokorrelaatiota.
seuraava taulukko on F-testi, lineaarisen regression F-testissä on nollahypoteesi, jonka mukaan kahden muuttujan välillä ei ole lineaarista suhdetta (toisin sanoen R2=0). Kun F = 156.2 ja 50 vapausastetta testi on erittäin merkittävä, joten voimme olettaa, että mallimme muuttujien välillä on lineaarinen suhde.


seuraavassa taulukossa on esitetty mallin regressiokertoimet, intercepti ja kaikkien kertoimien ja Interceptin merkitys. Havaitsemme, että lineaarinen regressioanalyysi arvioi lineaarisen regressiofunktion olevan y = -13.067 + 1.222
* x. huomaa, että tämä ei käännä siellä on 1.2 uutta murhaa tuhatta asukasta kohti, koska muutimme muuttujat.
jos suoritamme lineaarisen regressioanalyysin uudelleen alkuperäisillä muuttujilla, päädymme tulokseen y = 11.85 + 6.7*10-5 joka osoittaa, että jokaista 10 000: ta asukasta kohti odotamme näkevämme 6,7 uutta murhaa.
lineaarisessa regressioanalyysissämme kokeessa testataan nollahypoteesia, jonka mukaan kerroin on 0. T-testin mukaan sekä intercepti että muuttuja ovat erittäin merkittäviä (p < 0,001), joten voidaan sanoa, että ne eroavat nollasta.

tämä taulukko sisältää myös Beetapainot (jotka ilmaisevat riippumattomien muuttujien suhteellista merkitystä) ja kollineaarisuustilastot. Kuitenkin, koska meillä on vain 1 riippumaton muuttuja analyysissamme emme kiinnitä huomiota näihin arvoihin.
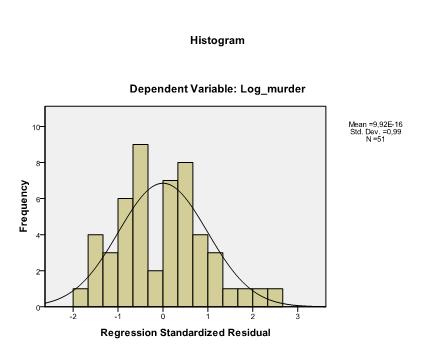
viimeinen asia, joka meidän täytyy tarkistaa, on jäännösten homoskedastisuus ja normaalius. Histogrammi osoittaa, että jäännökset likimäärin normaali jakauma. Z*predin ja z*presidin Q-Q-juoni osoittaa, että lineaarisessa regressioanalyysissä virhetermeillä ei ole taipumusta.