Korkeamman kertaluvun johdannaiset

päivitetty viimeksi 31.heinäkuuta 2021

korkeamman kertaluvun johdannaiset voivat kaapata tietoa funktiosta, jota ensimmäisen kertaluvun johdannaiset eivät yksinään pysty kaappaamaan.

ensimmäisen kertaluvun johdannaiset voivat kaapata tärkeitä tietoja, kuten muutosnopeuden, mutta yksinään ne eivät pysty erottamaan paikallisia minimejä tai maksimeja, joissa muutosnopeus on nolla molemmille. Useat optimointialgoritmit käsittelevät tätä rajoitusta hyödyntämällä korkeamman kertaluvun johdannaisten käyttöä, kuten Newtonin menetelmässä, jossa toisen kertaluvun derivaatoilla päästään optimointifunktion paikalliseen minimiin.

tässä opetusohjelmassa selviää, miten lasketaan korkeamman kertaluvun univariaatti-ja monimuuttujajohdannaiset.

kun olet suorittanut tämän opetusohjelman, tiedät:

• miten lasketaan univariaattifunktioiden korkeamman kertaluvun derivaatat.
• miten lasketaan monimuuttujafunktioiden korkeamman kertaluvun derivaatat.
• miten toisen kertaluvun johdannaisia voidaan hyödyntää koneoppimisessa toisen kertaluvun optimointialgoritmien avulla.

aloitetaan.

opetusohjelma yleiskatsaus

tämä opetusohjelma on jaettu kolmeen osaan; ne ovat:

• Univariaattifunktioiden korkeamman kertaluvun Derivaatat
• Monimuuttujafunktioiden korkeamman kertaluvun Derivaatat
• sovellus Koneoppimisessa

Univariaattifunktioiden korkeamman kertaluvun Derivaatat

ensimmäisen kertaluvun derivaatat, joiden olemme nähneet voivan antaa meille tärkeää tietoa funktiosta kuten sen hetkellinen muutosnopeus, myös korkeamman kertaluvun johdannaiset voivat olla yhtä hyödyllisiä. Toinen derivaatta voi esimerkiksi mitata liikkuvan kappaleen kiihtyvyyttä,tai se voi auttaa optimointialgoritmia erottamaan paikallisen maksimin ja paikallisen minimin.

univariaattifunktioiden korkeamman kertaluvun (toisen, kolmannen tai korkeamman) johdannaisten laskeminen ei ole kovin vaikeaa.

funktion toinen derivaatta on vain sen ensimmäisen derivaatan derivaatta. Kolmas derivaatta on toisen derivaatan derivaatta, neljäs derivaatta on kolmannen derivaatta ja niin edelleen.

– Page 147, Calculus for Dummies, 2016.

näin ollen korkeamman kertaluvun derivaattojen laskemiseen kuuluu yksinkertaisesti funktion erottelu toistuvasti. Sitä varten voimme yksinkertaisesti soveltaa valtasääntöä koskevaa tietoamme. Tarkastellaan esimerkiksi funktiota f (x) = x3 + 2×2 – 4x + 1. Sitten:

ensimmäinen derivaatta: f ”(x) = 3×2 + 4x-4

toinen derivaatta: f”(x) = 6x + 4

kolmas derivaatta: f” ” (x) = 6

neljäs derivaatta: f (4)(x) = 0

viides derivaatta: f (5) (x) = 0 jne.

olemme soveltaneet potenssisääntöä ensin F (x): ään saadaksemme sen ensimmäisen derivaatan, f'(x): n, sitten soveltaneet potenssisääntöä ensimmäiseen derivaattaan saadaksemme toisen, ja niin edelleen. Derivaatta menee lopulta nollaan, kun differentiaatiota sovelletaan toistuvasti.

tuote-ja osamääräsääntöjen soveltaminen pysyy voimassa myös korkeamman kertaluvun johdannaisten saamiseksi, mutta niiden laskenta voi muuttua messieriksi ja messieriksi kertaluvun kasvaessa. Yleinen Leibniz-sääntö yksinkertaistaa tehtävää tältä osin yleistämällä tuotesäännön:

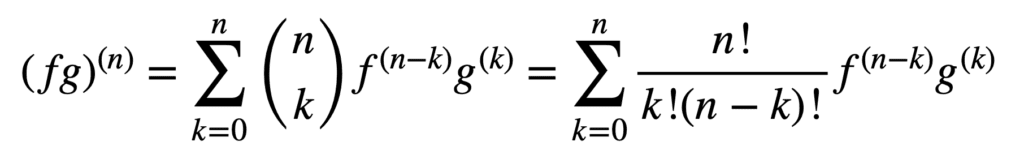
tässä termi, n! – k!n-k)!, on binomikerroin binomilauseesta, kun taas f (k) ja g(k) merkitsevät funktioiden kth-derivaatta, f ja g, vastaavasti.

näin ollen ensimmäisen ja toisen derivaatan löytäminen (ja siten N = 1: n ja N = 2: n korvaaminen) yleisen Leibnizin säännön mukaan antaa:

(fg) (1) = (fg) ” = f (1) g + f g(1)

(fg)(2) = (fg)” = f (2) g + 2F (1) g(1) + f g(2)

huomaa tuttu ensimmäinen johdannainen sellaisena kuin se määritellään tuotesäännössä. Leibnizin säännön avulla voidaan löytää myös rationaalifunktioiden korkeamman kertaluvun derivaatat, sillä osamäärä voidaan tehokkaasti ilmaista muodossa formula_1.

Monimuuttujafunktioiden korkeamman kertaluvun Derivaatat

monimuuttujafunktioiden korkeamman kertaluvun osittaisderivaatat määritellään analogisesti univariaattitapauksen kanssa: n: nnen kertaluvun osittaisderivaatta arvolle n > 1 lasketaan (N – 1): nnen kertaluvun osittaisderivaatta. Esimerkiksi ottamalla funktion toinen osittaisderivaatta kahdella muuttujalla saadaan neljä, toinen osittaisderivaatta: kaksi omaa osittaisderivaataa, fxx ja fyy, ja kaksi ristiosittaisderivaataa, fxy ja fyx.

”derivaatan” ottamiseksi on otettava osittainen derivaatta X: n tai y: n suhteen, ja siihen on neljä tapaa: x sitten x, x sitten y, y sitten x, y sitten y.

– sivu 371, yksi-ja Monimuuttujalaskenta, 2020.

tarkastellaan monimuuttujafunktiota f (x, y) = x2 + 3xy + 4y2, jolle haluaisimme löytää toisen osittaisderivaatan. Prosessi alkaa löytää sen ensimmäisen kertaluvun osittaisderivaatat, ensimmäinen: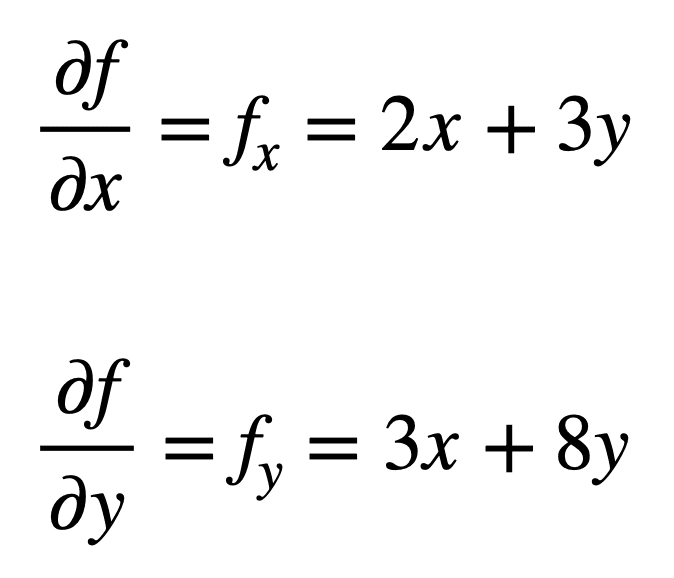

tämän jälkeen neljä, toisen kertaluvun osittaisderivaataa löydetään toistamalla osittaisderivaatojen löytämisprosessi. Omat osittaisderivaatat ovat helpoimmin löydettävissä, sillä toistamme vain osittaisderivaatioprosessin joko x: n tai y: n suhteen toisen kerran:

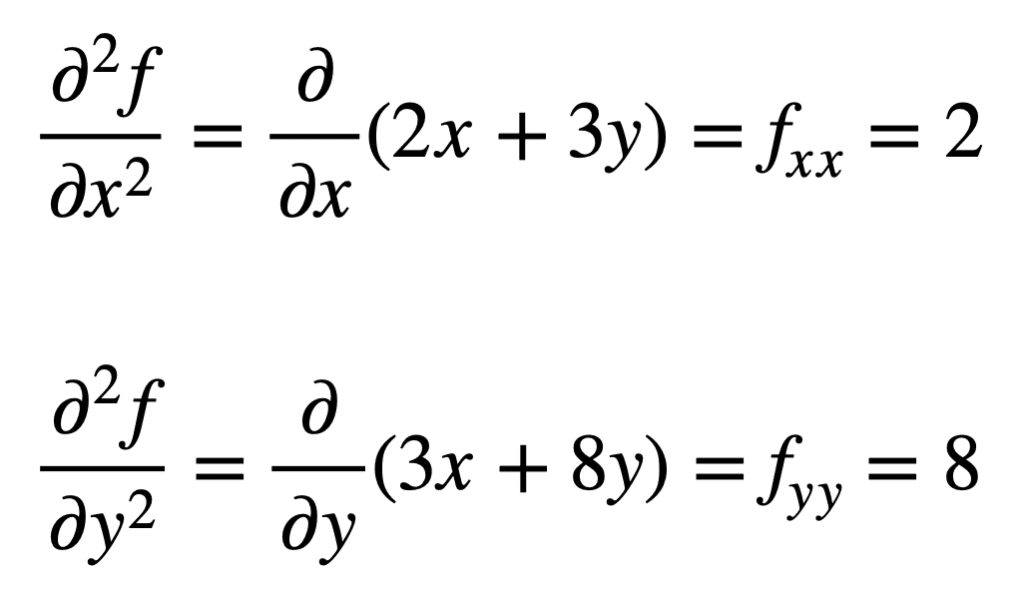
aiemmin löydetyn fx: n ristiosittaisderivaatta (eli osittaisderivaatta X: n suhteen) löytyy ottamalla tuloksen osittaisderivaatta Y: n suhteen, jolloin saadaan fxy. Vastaavasti kun otetaan fy: n osittainen derivaatta X: n suhteen, saadaan fyx:

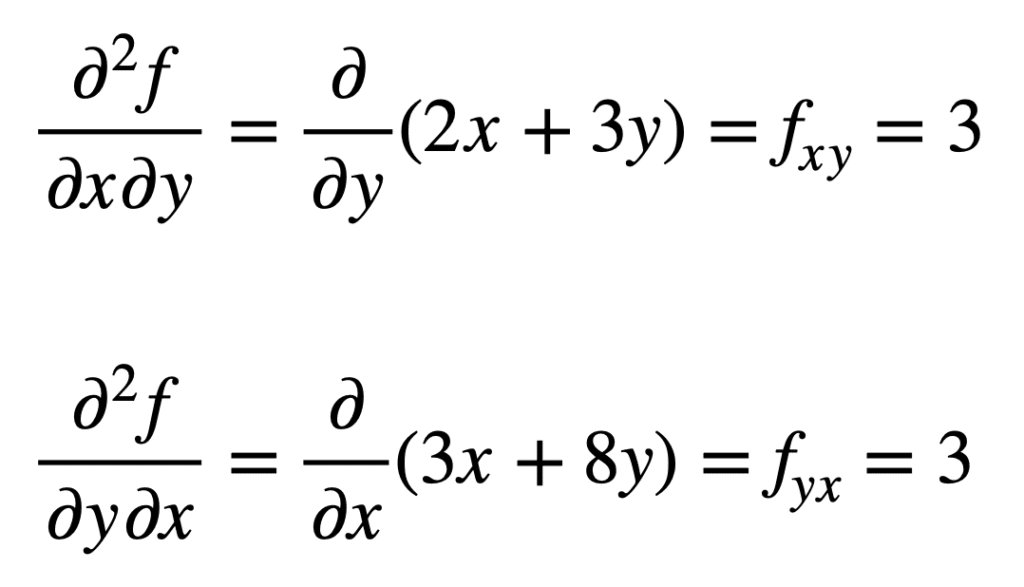
ei ole sattumaa, että ristin osittaisderivaatat antavat saman tuloksen. Tämä määritellään Clairaut ’ n lauseella, jonka mukaan niin kauan kuin ristin osittaisderivaatat ovat jatkuvia, ne ovat yhtä suuret.

sovellus Koneoppimisessa

koneoppimisessa käytetään useimmiten toisen kertaluvun derivaattaa. Olimme aiemmin maininneet, että toinen derivaatta voi antaa meille tietoa, jota ensimmäinen derivaatta ei yksinään pysty kaappaamaan. Erityisesti se voi kertoa, onko kriittinen piste paikallinen minimi vai maksimi (perustuu siihen, onko toinen derivaatta vastaavasti suurempi vai pienempi kuin nolla), jolle ensimmäinen derivaatta olisi muuten nolla molemmissa tapauksissa.

tätä tietoa hyödyntäviä toisen kertaluvun optimointialgoritmeja on useita, joista yksi on Newtonin menetelmä.

toisen kertaluvun tiedot sen sijaan mahdollistavat objektiivisen funktion neliöllisen approksimaation ja oikean porraskoon likiarvon paikallisen minimin saavuttamiseksi …

-Page 87, Algorithms for Optimization, 2019.

univariaattisessa tapauksessa Newtonin menetelmä käyttää toisen kertaluvun Taylorin sarjalaajennusta, jolla voidaan suorittaa kvadraattinen approksimaatio jonkin pisteen ympärillä objektiivisella funktiolla. Newtonin menetelmän päivityssääntö, joka saadaan asettamalla derivaatta nollaan ja ratkaisemalla juuri, sisältää jako-operaation toisen derivaatan avulla. Jos Newtonin menetelmää laajennetaan monimuuttuja-optimointiin, derivaatta korvataan gradientilla, kun taas toisen derivaatan käänteisarvo korvataan Hessenin matriisin käänteisellä.

käsittelemme erillisissä oppikirjoissa Hessenin ja Taylorin sarjojen likiarvoja, jotka hyödyntävät korkeamman kertaluvun johdannaisten käyttöä.

lisätietoja

tämä osio tarjoaa lisää resursseja aiheeseen, jos haluat mennä syvemmälle.

Kirjat

• yksi-ja Monimuuttujalaskenta, 2020.
• nukkien Calculus, 2016.
• Syväoppiminen, 2017.
• Optimointialgoritmit, 2019.

Yhteenveto

tässä oppaassa keksit, miten lasketaan korkeamman kertaluvun univariaatti-ja monimuuttujajohdannaiset.

nimenomaan opit:

• miten lasketaan univariaattifunktioiden korkeamman kertaluvun derivaatat.
• miten lasketaan monimuuttujafunktioiden korkeamman kertaluvun derivaatat.
• miten toisen kertaluvun johdannaisia voidaan hyödyntää koneoppimisessa toisen kertaluvun optimointialgoritmien avulla.