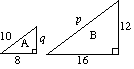laajentuminen on muutos, jossa kohde kartoittaa kuvan, joka on saman muotoinen mutta eri kokoinen. Esineen ja kuvan sanotaan olevan samanlaisia. Laajentuminen edellyttää laajentumiskeskusta ja mittakaavaa.
notaatio
E on laajentuminen, jonka keskikohta on O ja mittakerroin µ.
E: AB 
AB
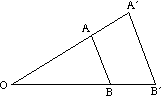
laajennuksen ominaisuudet
kolmion PQR kartat kolmion PQR: ään laajennuksen keskikohdalla O.
viivat ja niiden kuvat ovat aina yhdensuuntaisia.
esim.PQ on yhdensuuntainen PQ
Kulmakoko on invariantti.
esim.
PQR =
laajentuman keskusta on ainoa invariantti piste.
pituus ja pinta − ala eivät ole invariantteja, paitsi jos m = 1 tai-1.
eli laajentuminen ei ole isometria.
laajentuminen on suora muutos.
eli
PQR ja
jos μ on pituuden mittakerroin, mµ 2 on pinta-alan mittakerroin.
eri Mittakertoimet
alla olevassa kaaviossa esitetään useiden mittakertoimien vaikutus kolmion ABC: n laajentumiseen O-keskipisteen ympäri.
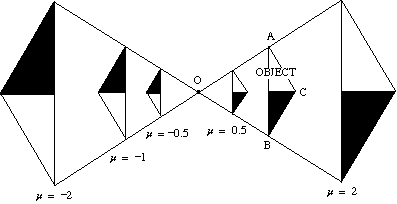
- jos mittakerroin on positiivinen, sekä kohde että kuva ovat samalla puolella keskustaa.
- jos mittakerroin on negatiivinen, kohde ja kuva ovat vastakkaisilla puolilla keskustaa.
Kuva on ylösalaisin.
katso esimerkkejä laajentumisista− 
Laajentumiskeskuksen sijainti
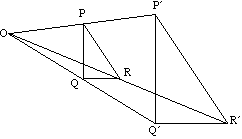
annettu kuva ja sen kuva laajentumiskeskuksen löytämiseksi:
1. Liity pisteeseen ja sen kuvaan.
2. Toista toinen kohta ja sen kuva.
3. Laajentumisen keskus on näiden linjojen risteyskohta.
vastaavat luvut
luvut ovat samanlaisia, jos ne ovat saman muotoisia.
- vastaavat luvut voidaan kartoittaa toisiinsa laajentumalla tai heijastuksen, vuorottelun tai käännöksen ja laajentumisen yhdistelmällä.
- vastaavien lukujen vastaavat kulmat ovat yhtä suuret.
- vastaavat puolet ovat verrannollisia toisiinsa.
tyyppi 1
YXZ on samanlainen kuin PQM, koska niillä vastaavat kulmat ovat yhtä suuret.
|
|
 |
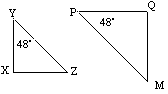YXZ voidaan kartoittaa arvoon PQM muunnosten yhdistelmällä.
Mittakerroin = µ = 
tyyppi 2
ABC on samanlainen kuin ADE, koska:
|
(DE on yhdensuuntainen BC) |
 |
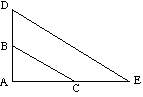ABC voidaan kartoittaa ADE laajennuksella.
Mittakerroin = µ = 
|
(a) (i) kaksi kolmiota A ja B ovat samanlaisia. Etsi p ja q. |
(a) (i) For a p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) kolmion a pinta-ala on 24 yksikköä2. |
(ii) Mittakerroin pinta-alalle = µ2 = 4 kolmion B pinta-ala = 4 x kolmion a pinta-ala |
|
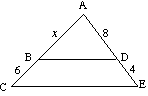
(B) Etsi x, jos BD on yhdensuuntainen CE: n kanssa |
(b)
  12x = 8 (x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B, scale factor = 2
ABD
Lataa interaktiivinen laskentataulukko (Microsoft Excel), joka näyttää heijastuksia, rotaatioita, käännöksiä ja suurennoksia.
(Windows-käyttäjät, Napsauta hiiren kakkospainikkeella ja ” tallenna kohde nimellä…”tallentaa tiedostot tietokoneeseen.)
