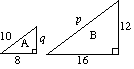Una ampliación es una transformación en la que un objeto se asigna a una imagen de la misma forma pero de diferente tamaño. El objeto y la imagen son similares. Una ampliación requiere un centro de ampliación y un factor de escala.
la Notación
E es una ampliación, con centro de ampliación de la S y el factor de escala µ.
E: AB 
AB
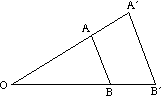
Propiedades de ampliación
El triángulo PQR se asigna al triángulo PQR bajo ampliación con centro O.
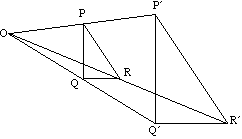
Las líneas y sus imágenes son siempre paralelas.
por ejemplo, PQ es paralelo a PQ
El tamaño del ángulo es invariante.
por ejemplo,
PQR =
El centro de ampliación es el único punto invariante.
La longitud y el área no son invariantes, excepto cuando m = 1 o − 1.
es decir, la ampliación no es una isometría.
La ampliación es una transformación directa.
es decir,
PQR y
Si μ es el factor de escala para la longitud, mµ 2 es el factor de escala para el área.
Diferentes factores de escala
El siguiente diagrama muestra el efecto de una variedad de factores de escala en la ampliación de un triángulo ABC sobre el centro O.
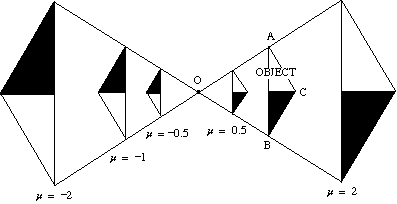
- Si el factor de escala es positivo, tanto el objeto como la imagen están en el mismo lado del centro.
- Si el factor de escala es negativo, el objeto y la imagen están en lados opuestos del centro.
La imagen está invertida.
Ver ejemplos de ampliaciones− 
Ubicación del Centro de la Ampliación
Dada una figura y su imagen, para encontrar el centro de la ampliación:
1. Unir un punto y su imagen.
2. Repita para otro punto y su imagen.
3. El centro de la ampliación es la intersección de estas líneas.
Figuras similares
Las figuras son similares si tienen la misma forma.
- Figuras similares se pueden mapear entre sí mediante una ampliación o mediante una combinación de reflexión, rotación o traslación y una ampliación.
- Los ángulos correspondientes de figuras similares son iguales.
- Los lados correspondientes son proporcionales entre sí.
Tipo 1
YXZ es similar a PQM, ya que tienen ángulos correspondientes iguales.
|
|
 |
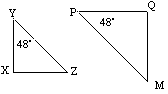YXZ puede ser asignado a PQM por una combinación de transformaciones.
Factor de escala = µ = 
Tipo 2
ABC es similar a ADE porque:
|
(DE es paralelo a BC) |
 |
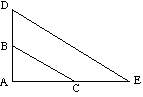ABC pueden ser mapeadas a ADE por una ampliación.
factor de Escala = µ = 
|
(a) (i) Los dos triángulos a y B son similares. Encuentra p y q. |
(a) i) Para A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
(ii) El área del triángulo A es de 24 unidades2. |
(ii) Factor de escala para área = µ2 = 4 Área del triángulo B = 4 x área del triángulo A |
|
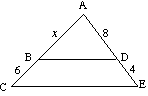
(b) Encontrar x, si BD es paralelo a CE |
(b) Para
  12x = 8 (x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B , factor de escala = 2
ABD
Descargue una hoja de cálculo interactiva (Microsoft Excel) que muestra reflexiones, rotaciones, traducciones y ampliaciones.
(Usuarios de Windows, haga clic derecho y » Guardar destino como…»para guardar los archivos en su computadora.)
