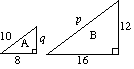Eine Vergrößerung ist eine Transformation, bei der ein Objekt einem Bild derselben Form, aber unterschiedlicher Größe zugeordnet wird. Das Objekt und das Bild sollen ähnlich sein. Eine Erweiterung erfordert ein Erweiterungszentrum und einen Skalierungsfaktor.
Notation
E ist eine Erweiterung, mit Vergrößerungszentrum O und Skalierungsfaktor µ.
E: AB 
AB
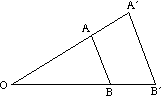
Eigenschaften der Vergrößerung
Dreieck PQR bildet Dreieck PQR unter Vergrößerung mit Zentrum O ab.
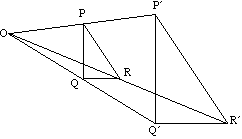
Linien und ihre Bilder sind immer parallel.
zB ist PQ parallel zu PQ
Die Winkelgröße ist invariant.
z.B.
PQR =
Der Vergrößerungsmittelpunkt ist der einzige invariante Punkt.
Länge und Fläche sind nicht invariant, außer wenn m = 1 oder − 1 ist.
d.h. Vergrößerung ist keine Isometrie.
Die Erweiterung ist eine direkte Transformation.
d. h.
PQR und
Wenn μ der Skalierungsfaktor für die Länge ist, ist mµ 2 der Skalierungsfaktor für die Fläche.
Verschiedene Skalenfaktoren
Das folgende Diagramm zeigt den Effekt verschiedener Skalenfaktoren auf die Vergrößerung eines Dreiecks ABC um den Mittelpunkt O.
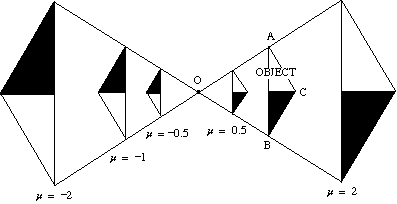
- Wenn der Skalierungsfaktor positiv ist, befinden sich sowohl das Objekt als auch das Bild auf derselben Seite des Zentrums.
- Wenn der Skalierungsfaktor negativ ist, befinden sich das Objekt und das Bild auf gegenüberliegenden Seiten des Zentrums.
Das Bild ist invertiert.
Siehe Beispiele für Erweiterungen − 
Lage des Vergrösserungszentrums
Angesichts einer Figur und ihres Bildes, um das Vergrösserungszentrum zu finden:
1. Verbinden Sie einen Punkt und sein Bild.
2. Wiederholen Sie dies für einen anderen Punkt und sein Bild.
3. Das Zentrum der Erweiterung ist der Schnittpunkt dieser Linien.
Ähnliche Figuren
Figuren sind ähnlich, wenn sie die gleiche Form haben.
- Ähnliche Figuren können durch eine Vergrößerung oder durch eine Kombination aus Reflexion, Rotation oder Translation und einer Vergrößerung aufeinander abgebildet werden.
- Die entsprechenden Winkel ähnlicher Figuren sind gleich.
- Die entsprechenden Seiten sind proportional zueinander.
Typ 1
YXZ ist ähnlich wie PQM, da sie entsprechende Winkel gleich haben.
|
|
 |
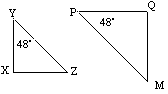YXZ kann durch eine Kombination von Transformationen auf PQM abgebildet werden.
Skalierungsfaktor = µ = 
Typ 2
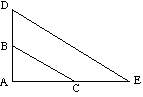
ABC ist ähnlich wie ADE, weil:
|
(DE ist parallel zu BC) |
 |
ABC kann durch eine Vergrößerung auf ADE abgebildet werden.
Skalierungsfaktor = µ = 
|
( a) (i) Die beiden Dreiecke A und B sind ähnlich. Finde p und q. |
( a) (i) Für A p = 2 × 10 p = 20 2 x q = 12 q = 6 |
|
( ii) Die Fläche des Dreiecks A beträgt 24 Einheiten2. |
( ii) Skalierungsfaktor für Fläche = µ2 = 4 Fläche des Dreiecks B = 4 x Fläche des Dreiecks A |
|
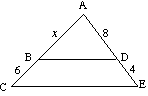
( b) Finde x, wenn BD parallel zu CE ist |
( b) Für
  12x = 8(x + 6) 12x = 8x + 48 4x = 48 x = 12 |
B, Skalierungsfaktor = 2
ABD
Laden Sie eine interaktive Tabelle (Microsoft Excel) herunter, die Reflexionen, Rotationen, Übersetzungen und Vergrößerungen zeigt.
( Windows-Benutzer, Rechtsklick und „Ziel speichern unter…“ um die Dateien auf Ihrem Computer zu speichern.)
