Højere ordens derivater

sidst opdateret den 31.Juli 2021

højere ordens derivater kan fange oplysninger om en funktion, som førsteordens derivater alene ikke kan fange.

førsteordensderivater kan fange vigtige oplysninger, såsom ændringshastigheden, men på egen hånd kan de ikke skelne mellem lokale minima eller Maksima, hvor ændringshastigheden er nul for begge. Flere optimeringsalgoritmer adresserer denne begrænsning ved at udnytte brugen af højere ordens derivater, f.eks.

i denne tutorial vil du opdage, hvordan du beregner univariate og multivariate derivater med højere orden.

efter at have afsluttet denne tutorial, vil du vide:

• Sådan beregnes de højere ordens derivater af univariate funktioner.
• Sådan beregnes de højere ordensderivater af multivariate funktioner.
• hvordan andenordensderivater kan udnyttes i maskinindlæring ved hjælp af andenordens optimeringsalgoritmer.

lad os komme i gang.

Tutorial Oversigt

denne tutorial er opdelt i tre dele; de er:

• højere Ordensderivater af Univariate funktioner
• højere Ordensderivater af Multivariate funktioner
• anvendelse i maskinlæring

højere Ordensderivater af Univariate funktioner

ud over førsteordensderivater, som vi har set, kan give os vigtige oplysninger om en funktion, såsom dens øjeblikkelige ændringshastighed, derivater med højere orden kan også være lige så nyttige. For eksempel kan det andet derivat måle accelerationen af et bevægeligt objekt, eller det kan hjælpe en optimeringsalgoritme med at skelne mellem et lokalt maksimum og et lokalt minimum.

beregning af højere ordens (anden, tredje eller højere) derivater af univariate funktioner er ikke så svært.

det andet derivat af en funktion er bare derivatet af dets første derivat. Det tredje derivat er derivatet af det andet derivat, det fjerde derivat er derivatet af det tredje og så videre.

– side 147, Calculus For Dummies, 2016.

derfor involverer beregning af højere ordensderivater simpelthen differentiering af funktionen gentagne gange. For at gøre det kan vi simpelthen anvende vores viden om magtreglen. Lad os overveje funktionen, f(h) = H3 + 2H2 – 4h + 1, som et eksempel. Derefter:

første derivat: f ‘(H) = 3H2 + 4H – 4

andet derivat: f”(H) = 6H4

tredje derivat: f”‘(H) = 6

fjerde derivat: f (4)(H) = 0

femte derivat: f (5)(H) = 0 osv.

det, vi har gjort her, er, at vi først har anvendt magtreglen på f(H) for at opnå dens første derivat, f'(H), derefter anvendt magtreglen på det første derivat for at opnå det andet osv. Derivatet vil til sidst gå til nul, da differentiering anvendes gentagne gange.

anvendelsen af produkt-og kvotientreglerne forbliver også gyldig ved opnåelse af højere ordensderivater, men deres beregning kan blive messier og messier, når ordren stiger. Den generelle Leibnisregel forenkler opgaven i dette aspekt ved at generalisere produktreglen til:

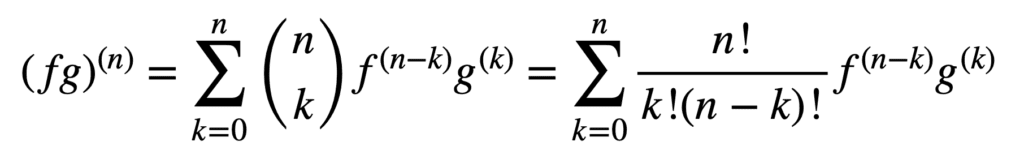
her, udtrykket, n! / k!(n-k)!, er binomialkoefficienten fra binomialsætningen, mens f (k) og g(k) betegner kth-derivatet af funktionerne, henholdsvis f og g.

derfor finder vi det første og andet derivat (og dermed erstatter n = 1 og n = 2) ved den generelle Leibnisregel:

(fg) (1) = (fg) ‘ = f (1) g + f g(1)

(fg) (2) = (fg)” = f (2) g + 2F(1) g(1) + f g (2)

Bemærk det velkendte første derivat som defineret af produktreglen. Leibnisreglen kan også bruges til at finde højere ordensderivater af rationelle funktioner, da kvotienten effektivt kan udtrykkes i et produkt af formen, f g-1.

højere Ordensderivater af Multivariate funktioner

definitionen af højere ordens partielle derivater af multivariate funktioner er analog med det univariate tilfælde: det nth-ordens partielle derivat for n > 1 beregnes som det partielle derivat af (n – 1)th-ordens partielle derivat. For eksempel resulterer det andet partielle derivat af en funktion med to variabler i fire, andet partielle derivater: to egne partielle derivater, f.eks.

for at tage et “derivat” skal vi tage et delvist derivat med hensyn til H eller y, og der er fire måder at gøre det på: H så H, H så y, y så y.

– side 371, Single and Multivariable Calculus, 2020.

lad os overveje den multivariate funktion, f(H, y) = H2 + 3HY + 4Y2, som vi gerne vil finde den anden delvise derivater. Processen starter med at finde sine første ordens partielle derivater, først: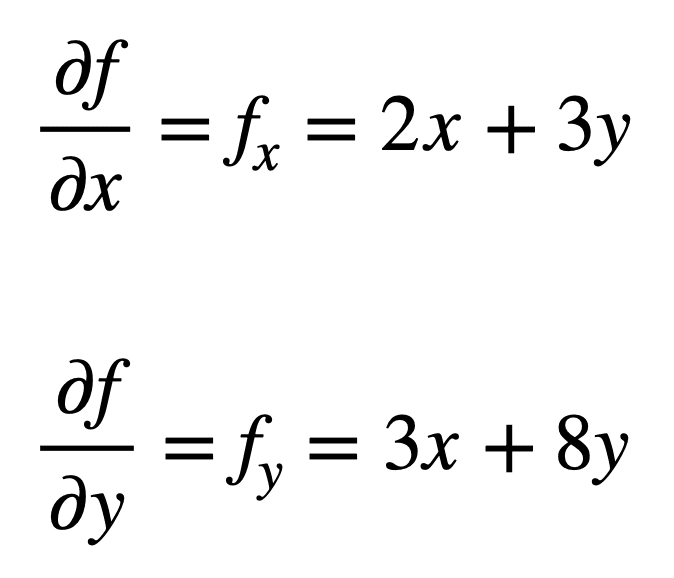

de fire, andenordens partielle derivater findes derefter ved at gentage processen med at finde de partielle derivater af de partielle derivater. De egne partielle derivater er de mest enkle at finde, da vi blot gentager den delvise differentieringsproces med hensyn til enten H eller y en anden gang:

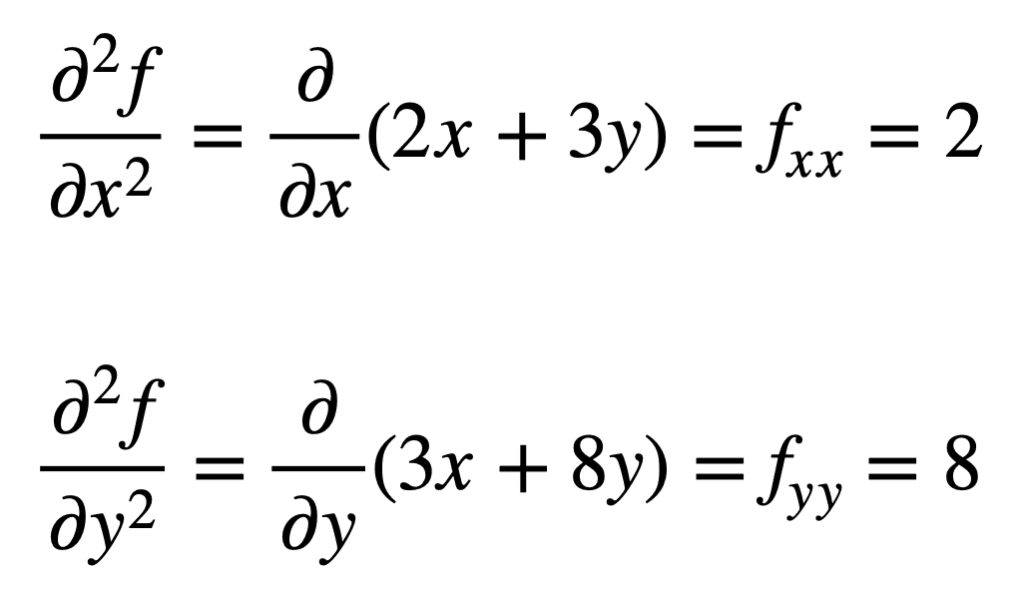
den delvise derivat af den tidligere fundne valuta (dvs.den delvise derivat med hensyn til den) findes ved at tage den delvise derivat af resultatet med hensyn til y, hvilket giver os valuta. På samme måde tager vi det delvise derivat af fy med hensyn til:

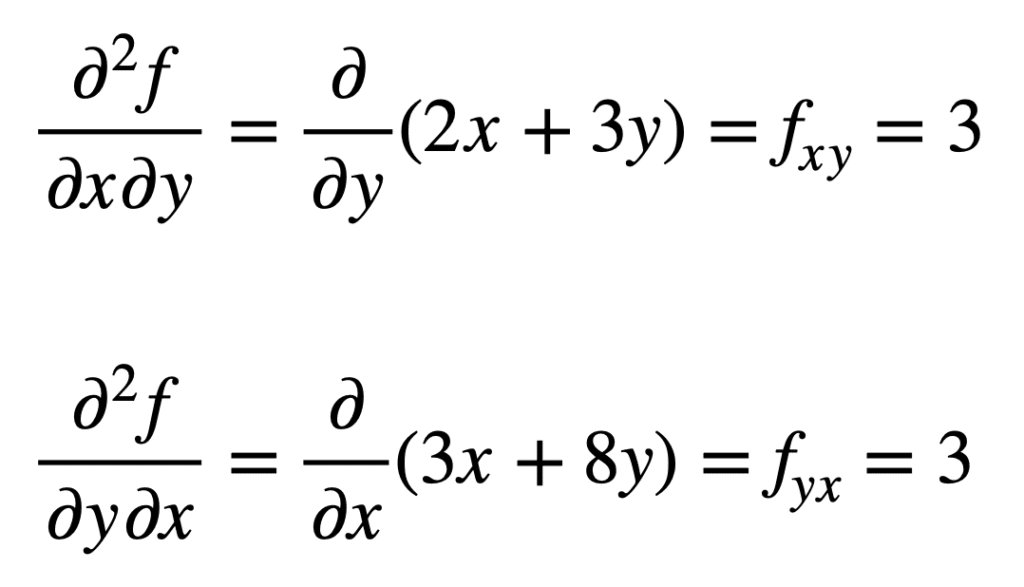
det er ikke tilfældigt, at de tværgående partielle derivater giver det samme resultat. Dette er defineret af Clairauts sætning, der siger, at så længe de tværgående partielle derivater er kontinuerlige, så er de ens.

anvendelse i maskinindlæring

i maskinindlæring er det andet ordens derivat, der mest bruges. Vi havde tidligere nævnt, at det andet derivat kan give os oplysninger, som det første derivat alene ikke kan fange. Specifikt kan det fortælle os, om et kritisk punkt er et lokalt minimum eller maksimum (baseret på om det andet derivat er henholdsvis større eller mindre end nul), for hvilket det første derivat ellers ville være nul i begge tilfælde.

der er flere andenordens optimeringsalgoritmer, der udnytter disse oplysninger, hvoraf den ene er Nyton ‘ s metode.

Andenordensinformation giver os på den anden side mulighed for at foretage en kvadratisk tilnærmelse af den objektive funktion og tilnærme den rigtige trinstørrelse for at nå et lokalt minimum …

-side 87, algoritmer til optimering, 2019.

i det univariate tilfælde bruger Nytons metode en andenordens Taylor-serieudvidelse til at udføre den kvadratiske tilnærmelse omkring et tidspunkt på den objektive funktion. Opdateringsreglen for Nyton ‘ s metode, som opnås ved at indstille derivatet til nul og løse for roden, involverer en divisionsoperation med det andet derivat. Hvis metoden udvides til multivariat optimering, erstattes derivatet af gradienten, mens det gensidige af det andet derivat erstattes med det inverse af den hessiske matrice.

vi skal dække Hessian og Taylor serien tilnærmelser, som udnytter brugen af højere ordens derivater, i separate tutorials.

yderligere læsning

dette afsnit giver flere ressourcer om emnet, hvis du ønsker at gå dybere.

bøger

• enkelt og multivariabel beregning, 2020.
• beregning for Dummies, 2016.
• Dyb Læring, 2017.
• algoritmer til optimering, 2019.

Resume

i denne vejledning opdagede du, hvordan du beregner univariate og multivariate derivater med højere orden.

specifikt lærte du:

• Sådan beregnes de højere ordens derivater af univariate funktioner.
• Sådan beregnes de højere ordensderivater af multivariate funktioner.
• hvordan andenordensderivater kan udnyttes i maskinindlæring ved hjælp af andenordens optimeringsalgoritmer.