dette eksempel er baseret på FBIs kriminalitetsstatistik fra 2006. Især er vi interesserede i forholdet mellem statens størrelse og antallet af mord i byen.
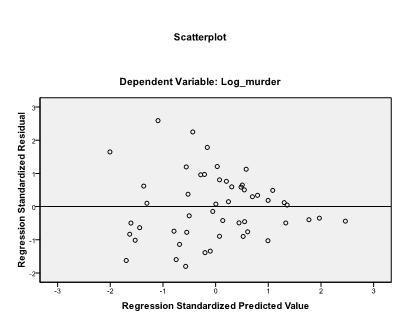
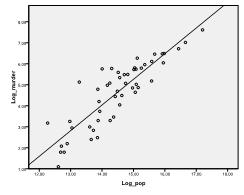
først skal vi kontrollere, om der er et lineært forhold i dataene. For det kontrollerer vi scatterplot. Scatter-plottet indikerer et godt lineært forhold, som giver os mulighed for at foretage en lineær regressionsanalyse. Vi kan også kontrollere Pearsons bivariate korrelation og finde ud af, at begge variabler er stærkt korrelerede (r = .959 med p < 0,001).

Opdag, hvordan vi hjælper med at redigere dine Afhandlingskapitler
tilpasning af teoretiske rammer, indsamling af artikler, syntese af huller, artikulering af en klar metode og dataplan og skrivning om de teoretiske og praktiske konsekvenser af din forskning er en del af vores omfattende afhandlingsredigeringstjenester.
- Bring afhandling redigering ekspertise til kapitel 1-5 i tide.
- Spor alle ændringer, og arbejd derefter med dig for at skabe videnskabelig skrivning.
- løbende støtte til adresse udvalg feedback, reducere revisioner.
for det andet skal vi kontrollere for multivariat normalitet. I vores eksempel finder vi, at multivariat normalitet måske ikke er til stede.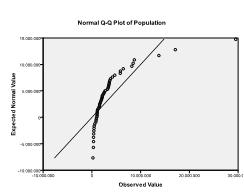
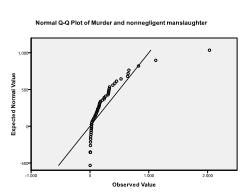
Kolmogorov-Smirnov-testen bekræfter denne mistanke (p = 0, 002 og p = 0.006). Gennemførelse af en ln-transformation på de to variabler løser problemet og etablerer multivariat normalitet (K-S test p = .991 og p = .543).
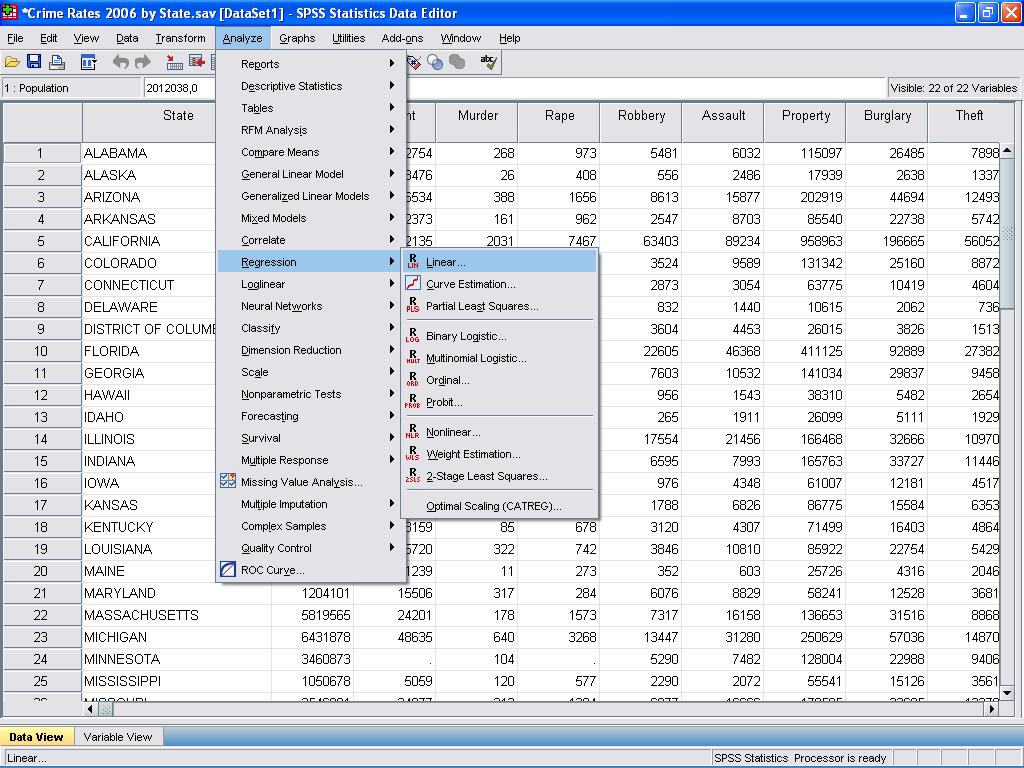
vi kan nu foretage den lineære regressionsanalyse. Lineær regression findes i SPSS i analyse / Regression / lineær…
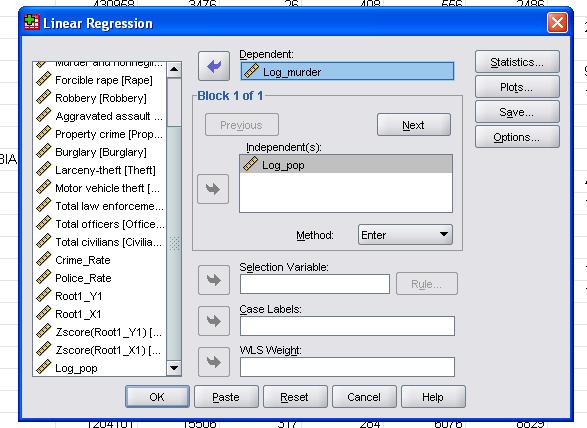
i dette enkle tilfælde skal vi blot tilføje variablerne log_pop og log_murder til modellen som afhængige og uafhængige variabler.
feltstatistikken giver os mulighed for at inkludere yderligere statistikker, som vi har brug for for at vurdere gyldigheden af vores lineære regressionsanalyse.
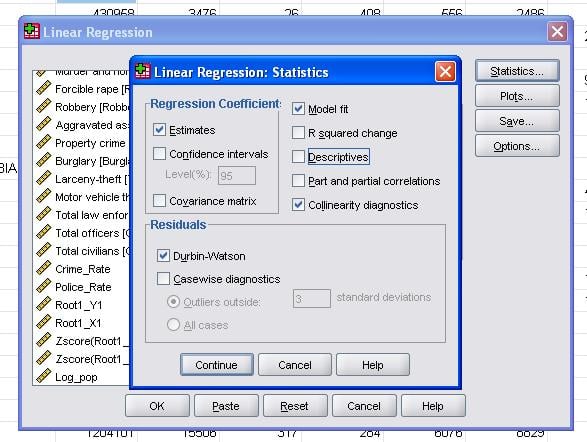
det anbefales desuden at inkludere kollinearitetsdiagnostik og Durbin-Vandson-testen for auto-korrelation. For at teste antagelsen om homoscedasticitet af rester inkluderer vi også et specielt plot i Plotmenuen.
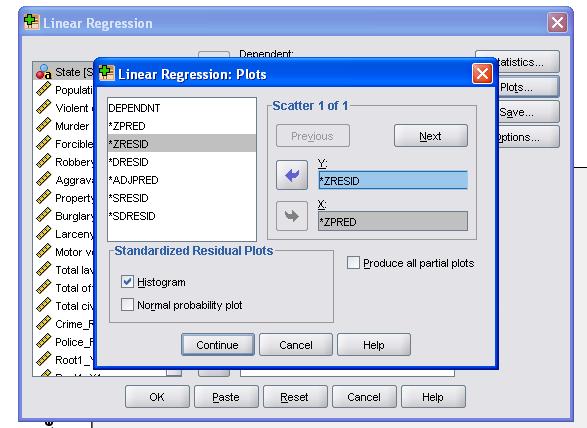
SPSS-syntaksen for den lineære regressionsanalyse er
REGRESSION
/mangler LISTEVIS
/statistik COEFF OUTS r ANOVA COLLIN TOL
/kriterier=PIN(.05)trut (.10)
/NOORIGIN
/afhængig Log_murder
/metode=indtast Log_pop
/SCATTERPLOT=(*SRESID ,*spred)
/rester DURBIN HIST(SRESID).
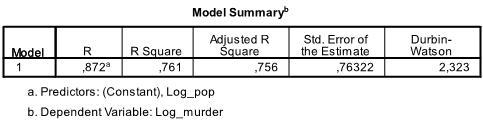
outputens første tabel viser modeloversigten og den samlede fit-statistik. Vi finder ud af, at den justerede R2 i vores model er 0, 756 med R2 = .761 det betyder, at den lineære regression forklarer 76.1% af variansen i dataene. D = 2.323, som er mellem de to kritiske værdier på 1.5 < d < 2.5, og derfor kan vi antage, at der ikke er nogen første ordens lineære auto-korrelation i dataene.
den næste tabel er F-testen, den lineære regressions F-test har nulhypotesen om, at der ikke er noget lineært forhold mellem de to variabler (med andre ord R2=0). F = 156.2 og 50 frihedsgrader testen er meget signifikant, så vi kan antage, at der er et lineært forhold mellem variablerne i vores model.

den næste tabel viser regressionskoefficienterne, skæringspunktet og betydningen af alle koefficienter og skæringspunktet i modellen. Vi finder ud af, at vores lineære regressionsanalyse estimerer den lineære regressionsfunktion til at være y = -13.067 + 1.222
* * * bemærk, at dette ikke oversætter i der er 1. 2 yderligere mord for hver 1000 Ekstra indbyggere, fordi vi Ln forvandlet variablerne.
hvis vi kørte den lineære regressionsanalyse igen med de originale variabler, ville vi ende med y = 11.85 + 6.7*10-5 hvilket viser, at for hver 10.000 yderligere indbyggere ville vi forvente at se 6,7 yderligere mord.
i vores lineære regressionsanalyse tester testen nulhypotesen om, at koefficienten er 0. T-testen finder ud af, at både intercept og variabel er meget signifikante (p < 0.001), og derfor kan vi sige, at de er forskellige fra nul.

denne tabel inkluderer også Beta-vægtene (som udtrykker den relative betydning af uafhængige variabler) og kollinearitetsstatistikken. Men da vi kun har 1 uafhængig variabel i vores Analyse, er vi ikke opmærksomme på disse værdier.
det sidste, vi skal kontrollere, er homoscedasticitet og normalitet af rester. Histogrammet indikerer, at resterne tilnærmer sig en normalfordeling. Det viser os, at der i vores lineære regressionsanalyse ikke er nogen tendens i fejlbetingelserne.