Dérivés d’ordre supérieur

Dernière mise à jour le 31 juillet 2021

Les dérivés d’ordre supérieur peuvent capturer des informations sur une fonction que les dérivés de premier ordre ne peuvent pas eux-mêmes capturer.

Les dérivées du premier ordre peuvent capturer des informations importantes, telles que le taux de variation, mais elles ne peuvent pas à elles seules faire la distinction entre les minima ou les maxima locaux, où le taux de variation est nul pour les deux. Plusieurs algorithmes d’optimisation répondent à cette limitation en exploitant l’utilisation de dérivées d’ordre supérieur, comme dans la méthode de Newton où les dérivées du second ordre sont utilisées pour atteindre le minimum local d’une fonction d’optimisation.

Dans ce tutoriel, vous découvrirez comment calculer des dérivées univariées et multivariées d’ordre supérieur.

Après avoir terminé ce tutoriel, vous saurez:

• Comment calculer les dérivées d’ordre supérieur des fonctions univariées.
• Comment calculer les dérivées d’ordre supérieur des fonctions multivariées.
• Comment les dérivées du second ordre peuvent être exploitées dans l’apprentissage automatique par des algorithmes d’optimisation du second ordre.

Commençons.

Aperçu du tutoriel

Ce tutoriel est divisé en trois parties; elles sont:

• Dérivées d’Ordre Supérieur de Fonctions Univariées
• Dérivées d’Ordre Supérieur de Fonctions Multivariées
• Application en Apprentissage Automatique

Dérivées d’Ordre Supérieur de Fonctions Univariées

En plus des dérivées de premier ordre, que nous avons vues peuvent nous fournir des informations importantes sur une fonction , comme son taux de variation instantané, les dérivées d’ordre supérieur peuvent également être tout aussi utiles. Par exemple, la dérivée seconde peut mesurer l’accélération d’un objet en mouvement, ou elle peut aider un algorithme d’optimisation à distinguer un maximum local d’un minimum local.

Calculer des dérivées d’ordre supérieur (deuxième, troisième ou supérieur) de fonctions univariées n’est pas si difficile.

La dérivée seconde d’une fonction n’est que la dérivée de sa dérivée première. La troisième dérivée est la dérivée de la dérivée seconde, la quatrième dérivée est la dérivée de la troisième, et ainsi de suite.

Par conséquent, le calcul de dérivées d’ordre supérieur implique simplement de différencier la fonction à plusieurs reprises. Pour ce faire, nous pouvons simplement appliquer notre connaissance de la règle du pouvoir. Considérons la fonction, f(x) = x3 + 2×2 – 4x + 1, à titre d’exemple. Alors :

Dérivée première: f'(x) = 3×2 + 4x–4

Dérivée seconde: f »(x) = 6x + 4

Dérivée troisième: f »‘(x) = 6

Dérivée quatrième: f(4) (x) = 0

Dérivée cinquième: f(5) (x) = 0 etc.

Ce que nous avons fait ici, c’est que nous avons d’abord appliqué la règle de puissance à f(x) pour obtenir sa dérivée première, f'(x), puis appliqué la règle de puissance à la dérivée première afin d’obtenir la seconde, et ainsi de suite. La dérivée finira par aller à zéro à mesure que la différenciation est appliquée à plusieurs reprises.

L’application des règles de produit et de quotient reste également valable pour obtenir des dérivées d’ordre supérieur, mais leur calcul peut devenir de plus en plus désordonné à mesure que l’ordre augmente. La règle générale de Leibniz simplifie la tâche dans cet aspect, en généralisant la règle du produit à:

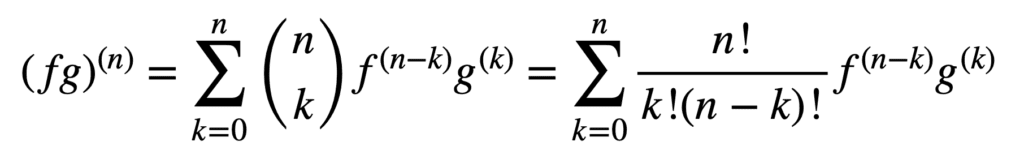
Ici, le terme, n! / k!(n-k)!, est le coefficient binomial du théorème binomial, tandis que f(k) et g(k) désignent la kème dérivée des fonctions, f et g, respectivement.

Par conséquent, trouver les dérivées première et seconde (et, par conséquent, substituer n = 1 et n = 2, respectivement), par la règle générale de Leibniz, nous donne:

(fg)(1) = (fg) ‘ = f(1) g + f g(1)

( fg)(2) = (fg)  » = f(2) g + 2f(1) g(1) + f g(2)

Notez la dérivée première familière telle que définie par la règle du produit. La règle de Leibniz peut également être utilisée pour trouver des dérivées d’ordre supérieur de fonctions rationnelles, puisque le quotient peut être efficacement exprimé en un produit de la forme, f g-1.

Dérivées d’ordre supérieur de Fonctions multivariées

La définition des dérivées partielles d’ordre supérieur de fonctions multivariées est analogue au cas univarié: la dérivée partielle du nième ordre pour n > 1, est calculée comme la dérivée partielle de la dérivée partielle du (n–1)th ordre. Par exemple, en prenant la deuxième dérivée partielle d’une fonction à deux variables, on obtient quatre deuxièmes dérivées partielles : deux dérivées partielles propres, fxx et fyy, et deux dérivées partielles croisées, fxy et fyx.

Pour prendre une « dérivée », il faut prendre une dérivée partielle par rapport à x ou y, et il y a quatre façons de le faire : x puis x, x puis y, y puis x, y puis y.

– Page 371, Calcul simple et multivariable, 2020.

Considérons la fonction multivariée, f(x, y) = x2 + 3xy + 4y2, pour laquelle nous aimerions trouver les deuxièmes dérivées partielles. Le processus commence par trouver ses dérivées partielles du premier ordre, d’abord: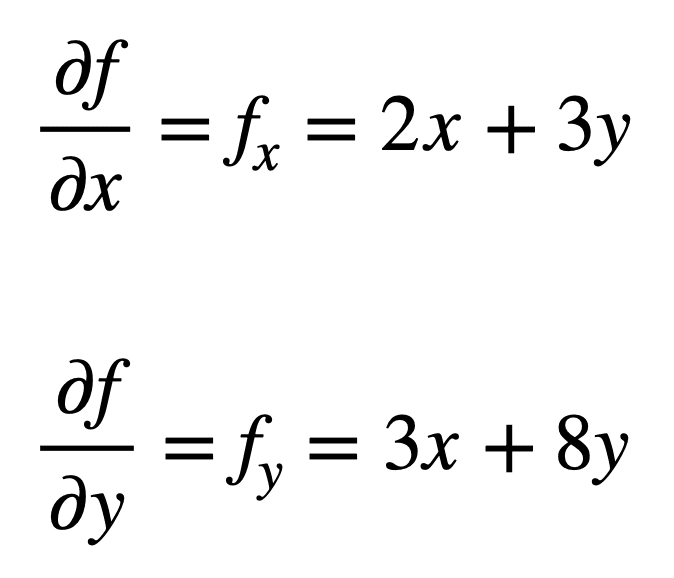

Les quatre dérivées partielles du second ordre sont ensuite trouvées en répétant le processus de recherche des dérivées partielles, des dérivées partielles. Les propres dérivées partielles sont les plus simples à trouver, car nous répétons simplement le processus de différenciation partielle, par rapport à x ou y, une deuxième fois:

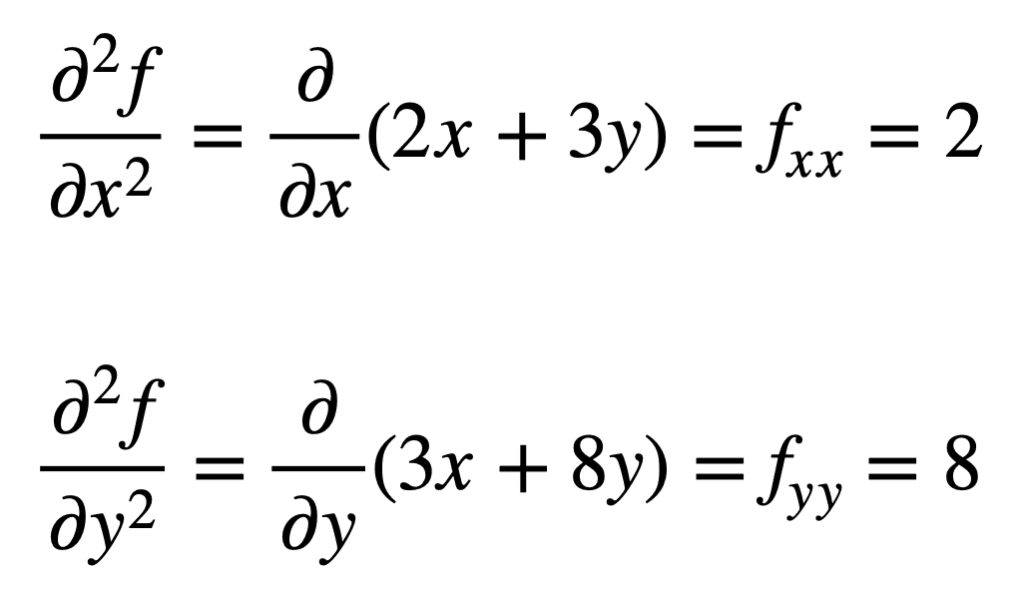
La dérivée partielle croisée du fx précédemment trouvé (c’est-à-dire la dérivée partielle par rapport à x) est trouvée en prenant la dérivée partielle du résultat par rapport à y, nous donnant fxy. De même, en prenant la dérivée partielle de fy par rapport à x, on obtient fyx:

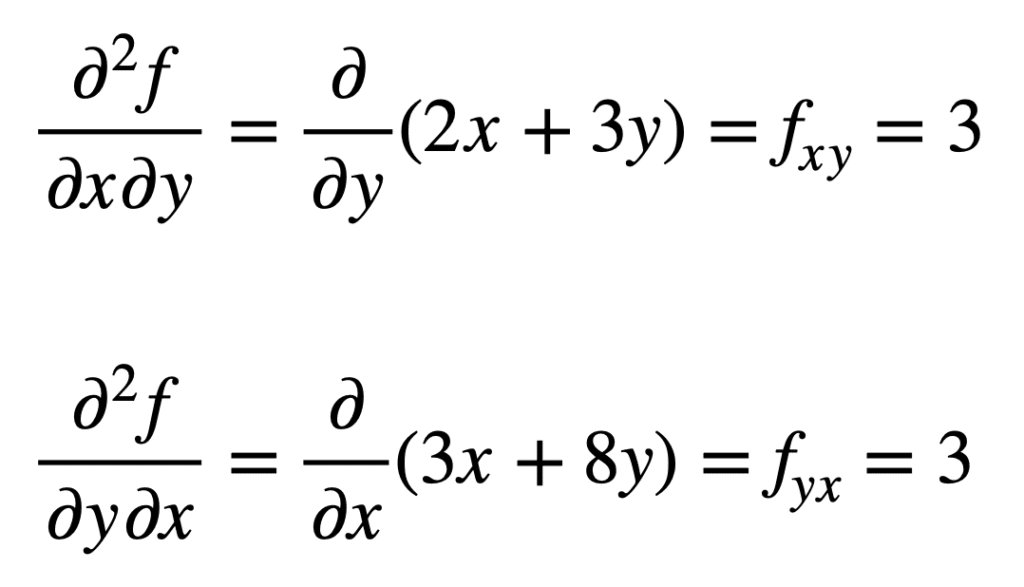
Ce n’est pas par hasard que les dérivées partielles croisées donnent le même résultat. Ceci est défini par le théorème de Clairaut, qui stipule que tant que les dérivées partielles croisées sont continues, elles sont égales.

Application en apprentissage automatique

En apprentissage automatique, c’est la dérivée du second ordre qui est principalement utilisée. Nous avions mentionné précédemment que la dérivée seconde peut nous fournir des informations que la dérivée première ne peut pas capturer à elle seule. Plus précisément, il peut nous dire si un point critique est un minimum ou un maximum local (selon que la dérivée seconde est supérieure ou inférieure à zéro, respectivement), pour lequel la dérivée première serait sinon nulle dans les deux cas.

Il existe plusieurs algorithmes d’optimisation du second ordre qui exploitent ces informations, dont la méthode de Newton.

Les informations de second ordre, en revanche, nous permettent de faire une approximation quadratique de la fonction objectif et d’approximer la bonne taille de pas pour atteindre un minimum local

– Page 87, Algorithmes d’optimisation, 2019.

Dans le cas univarié, la méthode de Newton utilise une expansion de la série de Taylor du second ordre pour effectuer l’approximation quadratique autour d’un point de la fonction objectif. La règle de mise à jour de la méthode de Newton, qui est obtenue en mettant la dérivée à zéro et en résolvant pour la racine, implique une opération de division par la dérivée seconde. Si la méthode de Newton est étendue à l’optimisation multivariée, la dérivée est remplacée par le gradient, tandis que l’inverse de la dérivée seconde est remplacé par l’inverse de la matrice de Hesse.

Nous couvrirons les approximations des séries de Hesse et de Taylor, qui tirent parti de l’utilisation de dérivées d’ordre supérieur, dans des tutoriels séparés.

Lectures supplémentaires

Cette section fournit plus de ressources sur le sujet si vous cherchez à aller plus loin.

Livres

• Calcul simple et multivariable, 2020.
• Calcul pour les nuls, 2016.
• Apprentissage profond, 2017.
• Algorithmes d’optimisation, 2019.

Résumé

Dans ce tutoriel, vous avez découvert comment calculer des dérivées univariées et multivariées d’ordre supérieur.

Plus précisément, vous avez appris:

• Comment calculer les dérivées d’ordre supérieur des fonctions univariées.
• Comment calculer les dérivées d’ordre supérieur des fonctions multivariées.
• Comment les dérivées du second ordre peuvent être exploitées dans l’apprentissage automatique par des algorithmes d’optimisation du second ordre.